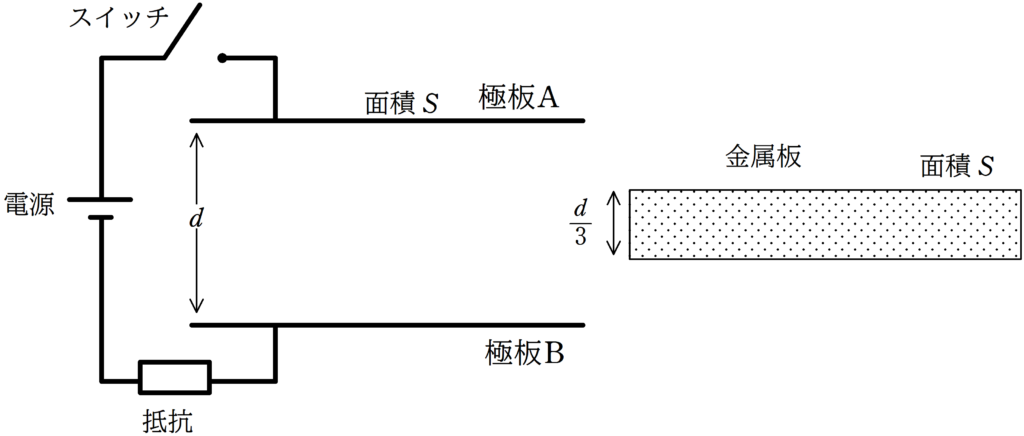
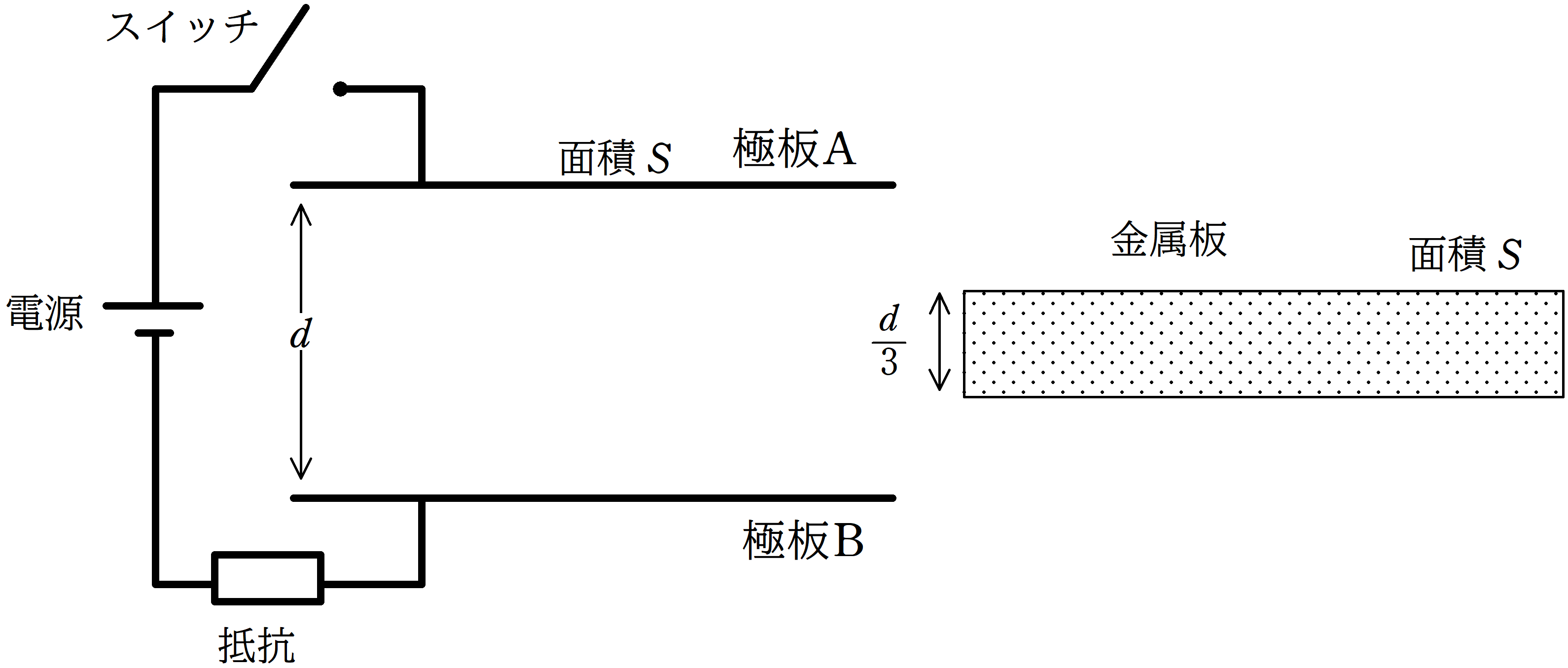
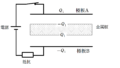
起電力$V_{0}$の電源,スイッチ,抵抗と面積$S$の極板A,Bによってつくられた平行平板コンデンサーが上図のように接続されている.
極板A,Bの距離は$d$に固定されており,真空の誘電率を$\varepsilon_{0}$とする.
なお,空気中での誘電率も真空と同じであるとみなすことができるとしてよい.
スイッチを閉じて十分時間が経つと,コンデンサーに電荷$Q_{0}$が蓄えられた.
その後,スイッチを開いてからゆっくりと,面積$S$,厚さ$\dfrac{d}{3}$の金属板を極板A,Bの中央に極板と平行に挿入した.
このとき,次の問いに答えよ.
ただし,解答には$\varepsilon_{0}$,$d$,$S$,$V_{0}$を用いよ.
(1) $Q_{0}$を求めよ.
(2) コンデンサーと金属板の間の電場の大きさ$E_{1}$を求めよ.
(3) 極板AB間の電位差$V_{1}$を求めよ.
(4) 金属板挿入後のコンデンサーの電気容量$C_{1}$を求めよ.
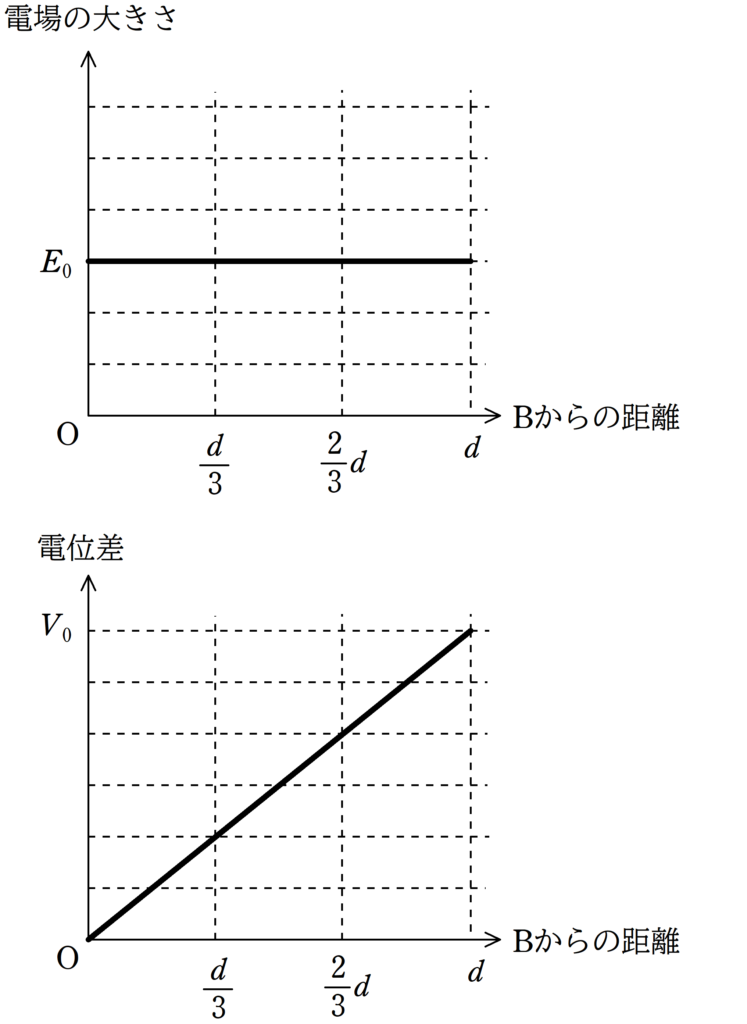
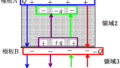
(5) 金属板を挿入する前のBからの距離とコンデンサー内の電場の大きさの関係のグラフ,および,Bからの距離とBを基準とした電位の関係は上図のようであった.金属板を挿入後のグラフをかけ.
<解答>
(1)

コンデンサーの基本式を立てることで,電荷$Q_{0}$を求めましょう.
コンデンサーの間の電圧は電源の電圧$V_{0}$と同じだね.
次の2式を確認しましょう.
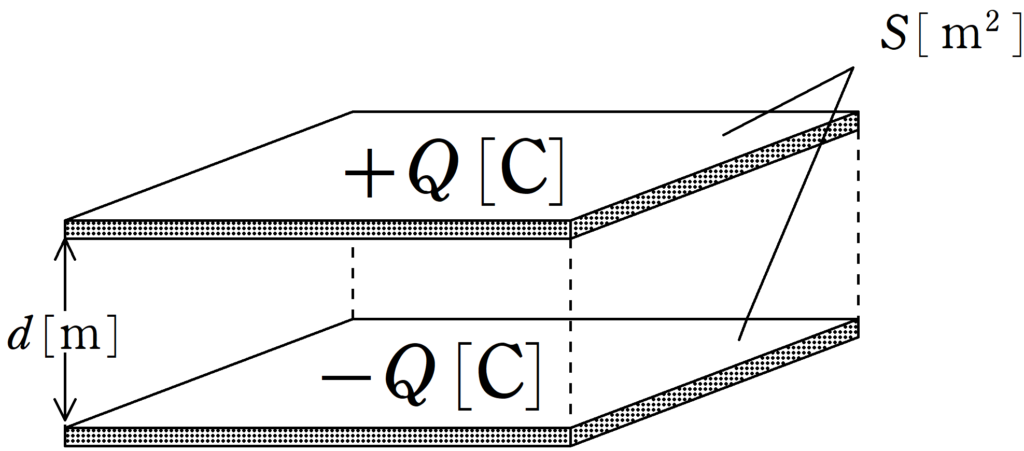
面積$S[\rm m^2]$の平らな導体板2枚を距離$d[\rm m]$だけ隔てて固定する.
真空の誘電率を$\varepsilon_{0}[\rm F/m]$とする.真空中において,このコンデンサーの電気容量$C_{0}[\rm F]$は次のようになる.
$C_{0}=\varepsilon_{0}\dfrac{S}{d}$
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
★ コンデンサーの基本式
電気容量$C_{0}$は
$C_{0}=\varepsilon_{0}\dfrac{S}{d}$
コンデンサーの基本式から
$Q_{0}=C_{0}V_{0}=\varepsilon_{0}\dfrac{S}{d}V_{0}$
答え:$Q_{0}=\varepsilon_{0}\dfrac{S}{d}V_{0}$
(2)

スイッチを切っているので,極板A,Bに蓄えられている電荷は変化しないね.
平面に分布された電荷がつくる電場は次の式のように,極板の電荷と面積で決まります.
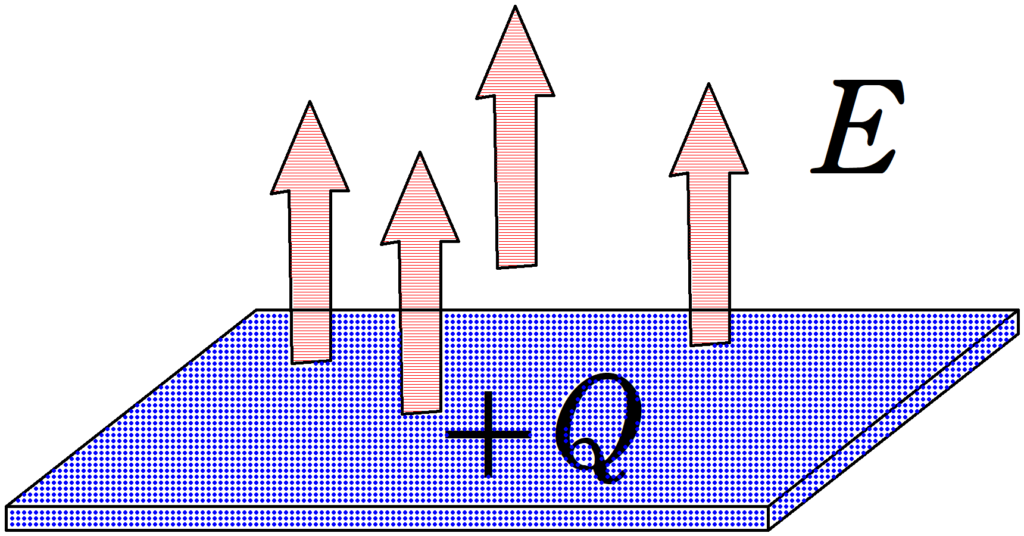
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.

さらに,金属板を挿入すると,金属板の中の自由電子が移動し,金属板内部の電場が0になるように,導体表面に電荷が分布します.
金属板に分布した電荷は,極板Aと金属板の間,および極板Bと金属板の間の電場には影響しません.
こちらの記事でも書いてるので確認しておいてください.
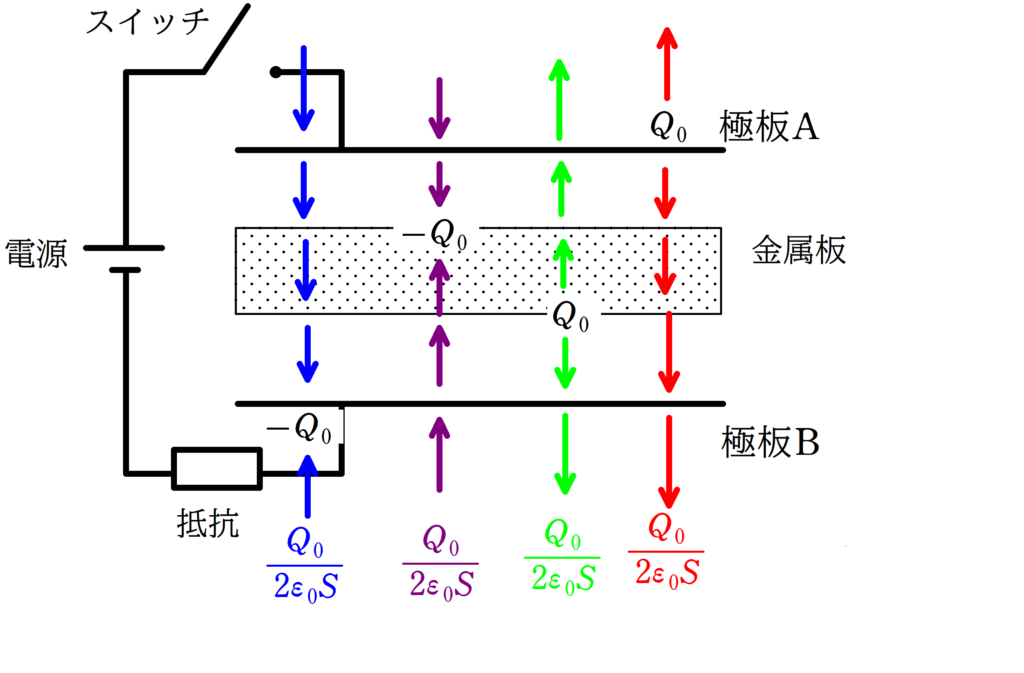
★ 板Aと金属板,および板Bと金属板の間の電場の大きさについて
$\eqalign{E_{1}&=\dfrac{Q_{0}}{2\varepsilon_{0}S}+\dfrac{Q_{0}}{2\varepsilon_{0}S}-\dfrac{Q_{0}}{2\varepsilon_{0}S}+\dfrac{Q_{0}}{2\varepsilon_{0}S}\\&=\dfrac{Q_{0}}{\varepsilon_{0}S}\\&=\dfrac{1}{\varepsilon_{0}S}\varepsilon_{0}\dfrac{S}{d}V_{0}\\&=\dfrac{V_{0}}{d}}$
答え:$E_{1}=\dfrac{V_{0}}{d}$
(3)

電場と電位差の関係は次のようになります.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$
★ AB間の電位差$V_{1}$について
$\eqalign{V_{1}&=E_{1}\cdot \dfrac{d}{3}+0\cdot \dfrac{d}{3}+E_{1}\cdot \dfrac{d}{3}\\&=\dfrac{2E_{1}}{3}d\\&=\dfrac{2}{3}V_{0}}$
答え:$V_{1}=\dfrac{2}{3}V_{0}$
(4)

コンデンサーの電気容量は,金属板の厚さの分だけ距離が縮んだと考えることができるんだよね.
または,$\dfrac{Q_{0}}{V_{1}}$を調べてもいいよ.
★ 金属板挿入後の電気容量$C_{1}$
$C_{1}=\varepsilon_{0}\dfrac{S}{\dfrac{2}{3}d}=\varepsilon_{0}\dfrac{3S}{2d}$
(5)

これまでの考察から電場と電位のグラフは次のようになります.
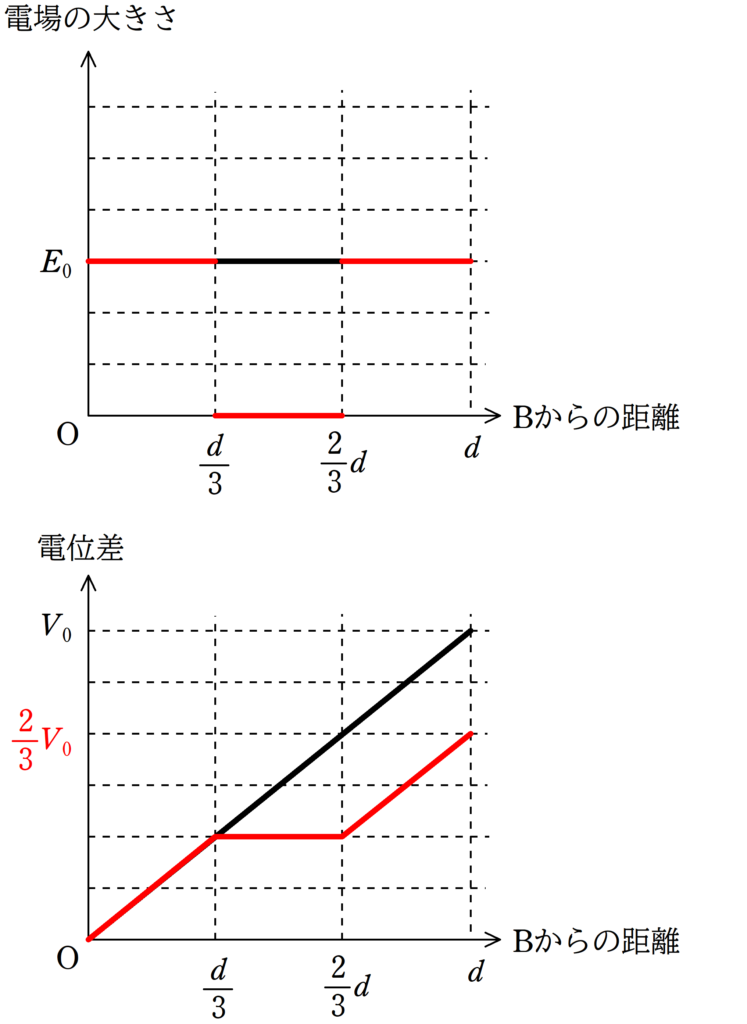

もう少しテクニック的な処理もできますが,ここでは一つ一つ丁寧に考えてみました.

コメント
[…] コンデンサー演習1 金属板の挿入 直列型 スイッチを開く問題起電力$V_… 問題 […]
[…] コンデンサー演習1 金属板の挿入 直列型 スイッチを開く問題起電力$V_… […]