
平行板コンデンサーに導体(金属板)を挿入すると,電気容量が変化するんだよね?
結論は次のようになるってことは知っているけど,なんでこんなふうになるうだろう??
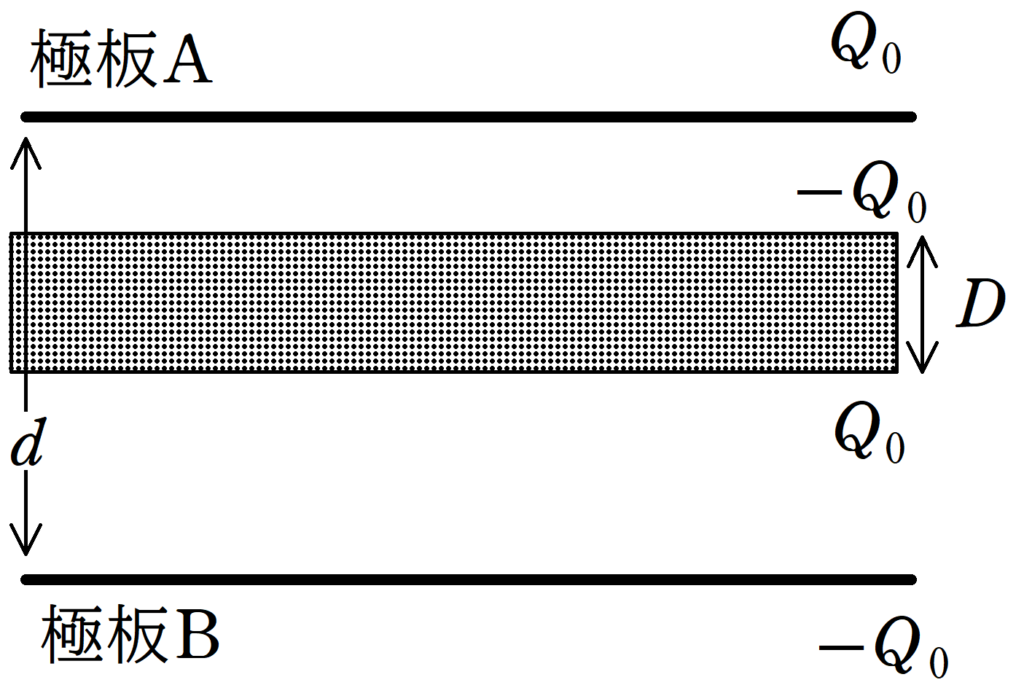
2枚の極板A,Bによってつくられた平行板コンデンサーに帯電していない厚さ$D$の導体板を挿入する.
極板A,Bの間隔を$d$,極板の面積を$S$,真空の誘電率を$\varepsilon_{0}$とすると,このコンデンサーの電気容量$C$は次のようになる.
$C=\varepsilon_{0}\dfrac{S}{d-D}$
これは,金属の厚さの分だけ,極板A,Bの間隔が縮まった考えることもできる.

それでは,今回は導体板を挿入することによって何が変化するのかを,次の2つの場合について調べてみましょう.
1.電源を取り外した状態でコンデンサー内部に導体板を挿入する.
2.電源をつないだまま,コンデンサー内部に導体板を挿入する.
1.電源を取り外した状態でコンデンサー内部に導体板を挿入する.
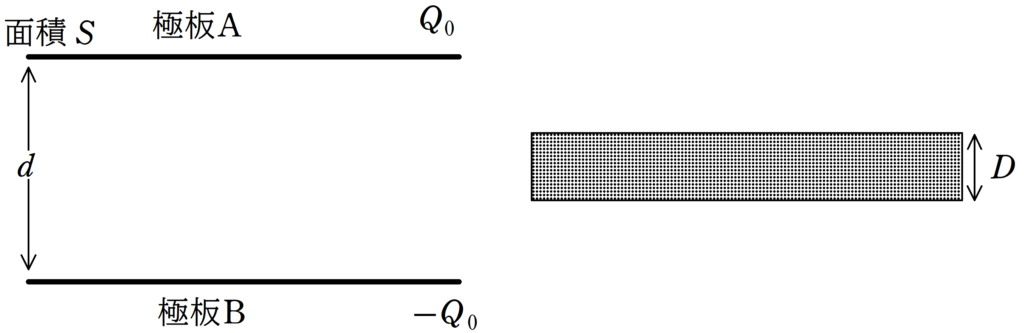

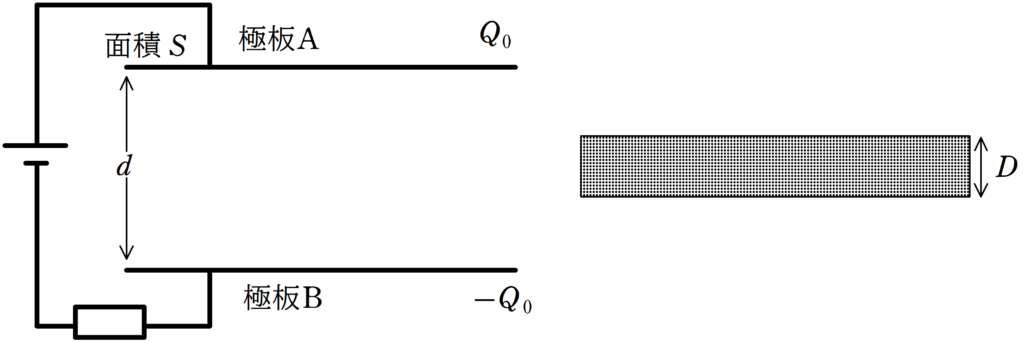
面積$S$の極板A,Bを距離$d$隔てて平行に固定します.
真空の誘電率を$\varepsilon_{0}$とし,真空とみなせる場所にあると仮定しましょう.
極板A,Bによってつくられたコンデンサーにはあらかじめ電荷$Q_{0}$が蓄えられています.極板Aが$Q_{0}$,極板Bが$-Q_{0}$に帯電しています.
この状態から極板A,Bと平行になるように,厚さが$D$,面積$S$の導体をコンデンサーに挿入します.
極板A,Bは孤立しているため,電荷の移動は起こりません.
しかし,挿入した導体は極板A,Bによって生じた電場の影響で自由電子が移動し,導体内部の電場を0にするように導体表面に電荷が分布します.
このような現象を静電誘導といいます.
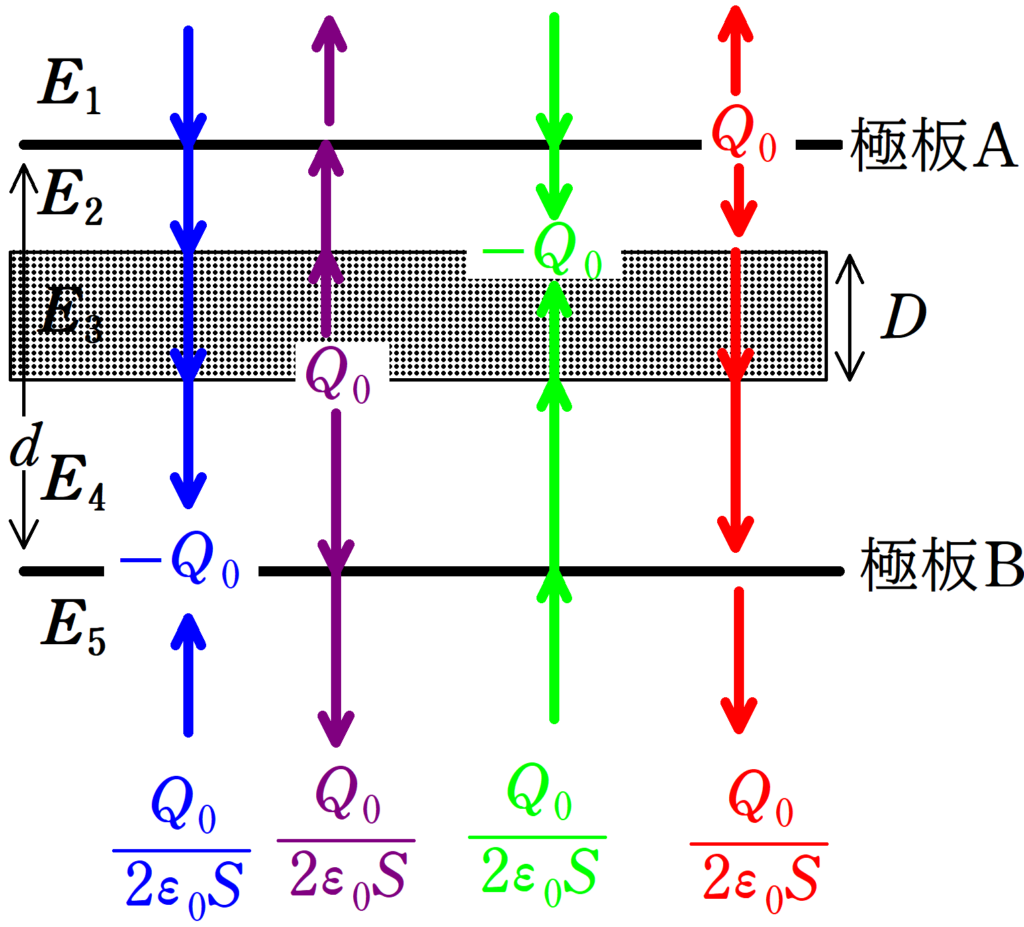

上図のように,導体のA側部分には電荷$-Q_{0}$が,導体のB側部分には電荷$Q_{0}$が帯電しています.
平面に分布された電荷がつくる電場は次のようになるんでしたね.
このことから,各電荷がつくる電場を足し合わせていきます.
下向きを正とすれば,上図の領域の電場$E_{1}$,$E_{2}$,$E_{3}$,$E_{4}$,$E_{5}$は次のようになります.
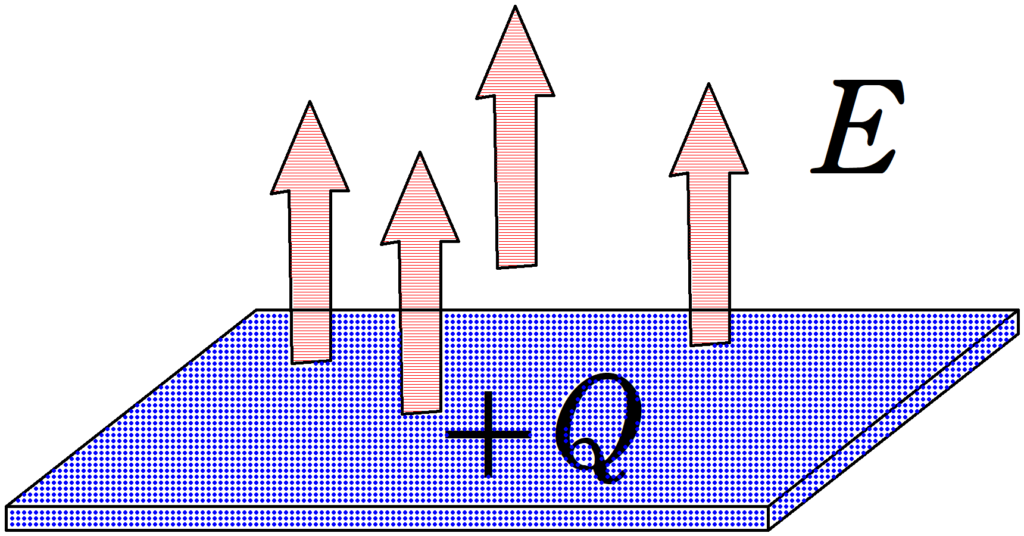
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.
★ 電場の重ね合わせの原理より
$E_{1}=\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}=0$
$E_{2}=\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}=\dfrac{Q}{\varepsilon_{0}S}$
$E_{3}=\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}=0$
$E_{4}=\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}=\dfrac{Q}{\varepsilon_{0}S}$
$E_{5}=-\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}-\dfrac{Q}{2\varepsilon_{0}S}+\dfrac{Q}{2\varepsilon_{0}S}=0$
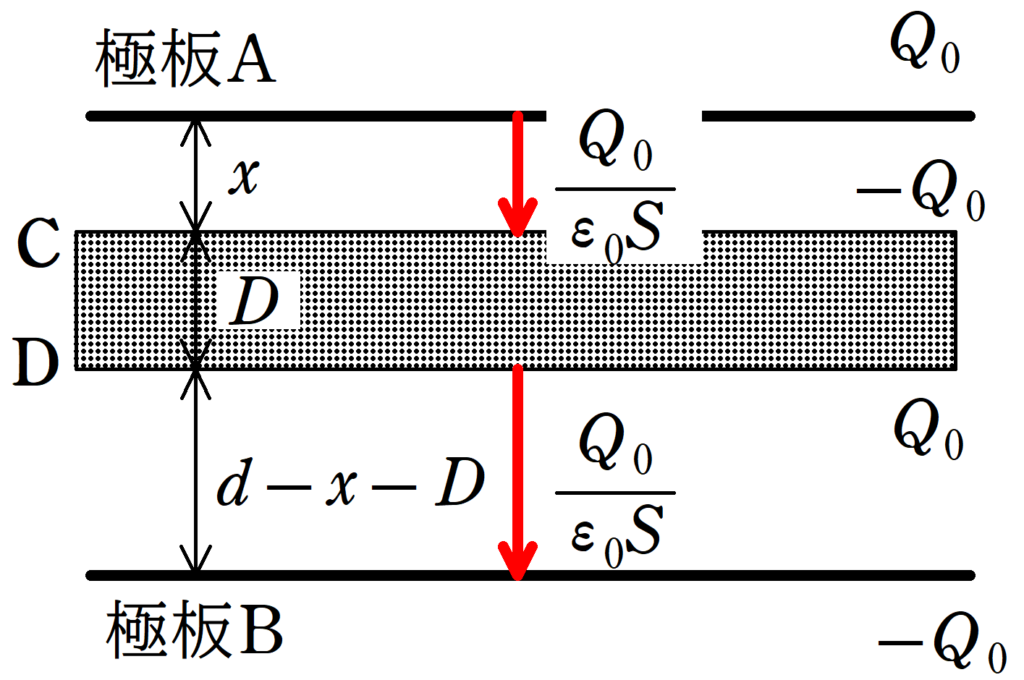

結論,上図の赤色の矢印の部分に電場が生じているだけになります.
そこで,AC,CD,DBの電位差の合計を計算してみましょう.
電場と電位差の関係は次のようになることを確認しておきましょう.
電場の大きさを$E$,距離$\Delta x$の電位差を$\Delta V$とするとき,次の関係が成り立つ.
$E=\left|\dfrac{\Delta V}{\Delta x}\right|$
★ AB間の電位差について
AB間の電位差を$V_{\rm AB}$として
$\eqalign{V_{\rm AB}&=\dfrac{Q}{\varepsilon_{0}S}\cdot x+0\cdot D+\dfrac{Q}{\varepsilon_{0}S}\cdot (d-x-D)\\&=\dfrac{Q}{\varepsilon_{0}S}(d-D) \dots (\ast)}$

そして,コンデンサーの電気容量の定義式を使って,電気容量を計算してみましょう.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
★ コンデンサーの基本式
$(\ast)$より
$C=\dfrac{Q}{V_{\rm AB}}=\varepsilon_{0}\dfrac{S}{d-D}$

確かに,導体板の厚さの分だけ,距離が縮んだ式になっているね.
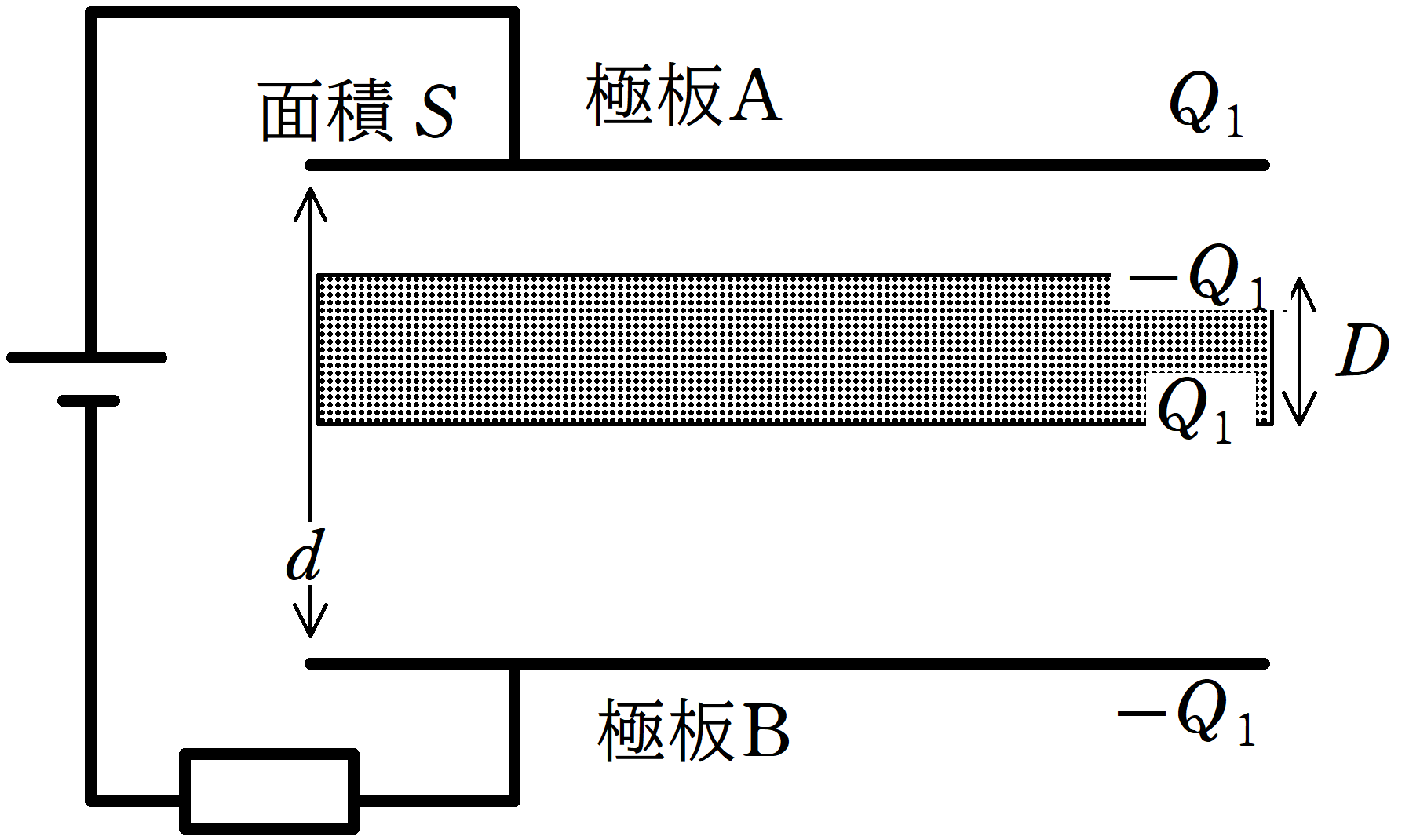
2.電源をつないだまま,コンデンサー内部に導体板を挿入する.

今度は起電力$V_{0}$の電源をつないだまま,ゆっくりと導体板を挿入します.
すると,極板AとBの電圧が電源の電圧$V_{0}$と同じになるように,極板A,Bの電荷が少しずつ移動していきます.
導体板を挿入する前のコンデンサーの式は,次のようになります.
$Q_{0}=\varepsilon_{0}\dfrac{S}{d}V_{0}$
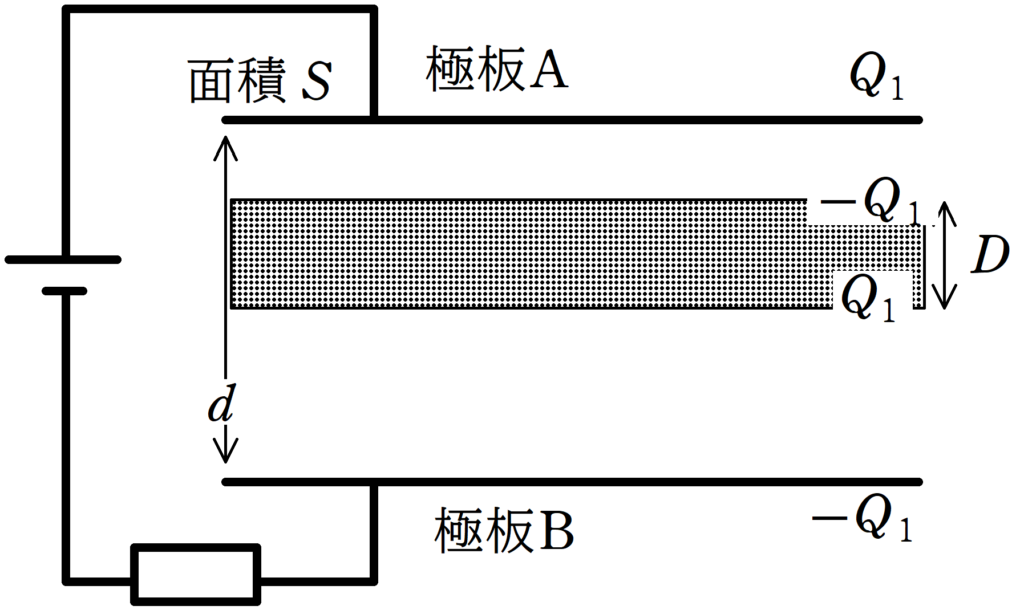

導体板を挿入した後に極板A,Bに蓄えられた後の電荷をそれぞれ$Q_{1}$,$-Q_{1}$とすると,静電誘導により,導体板のA側部分は$-Q_{1}$に導体板のB側部分は$Q_{1}$に帯電します.
すると,さきほどと同様に電場を考えれば,次のようになります.
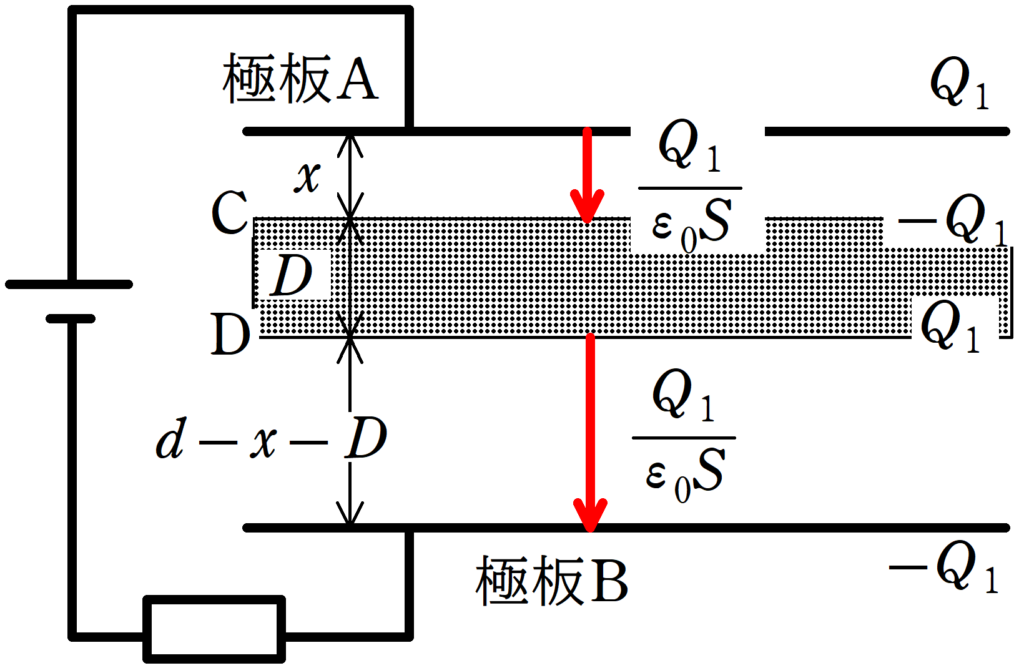

AとCの間の電場の大きさは$\dfrac{Q_{1}}{\varepsilon_{0}S}$,DとBの間の電場の大きさも$\dfrac{Q_{1}}{\varepsilon_{0}S}$で,その他の場所は電場0です.
極板ABの電位差は常に電源と同じ$V_{0}$であることを考慮して,次の式が成り立ちます.
今回もAC間の距離を$x$としましょう.
★ AとBの間の電位差
$\eqalign{V_{0}&=\dfrac{Q_{1}}{\varepsilon_{0}S}\cdot x+0\cdot D+\dfrac{Q_{1}}{\varepsilon_{0}S}\cdot (d-x-D)\\&=\dfrac{Q_{1}}{\varepsilon_{0}S}(d-D)}$
コンデンサーの電気容量の定義式より
$C_{1}=\dfrac{Q_{1}}{V_{0}}=\varepsilon_{0}\dfrac{S}{d-D}$

やっぱり,導体板の厚さの分だけ距離が縮んだ式になっているね.
最後にもう一度確認しておきましょう.
帯電していない導体板をコンデンサー内にいれると次のように電気容量の式をかくことができるんだね.

2枚の極板A,Bによってつくられた平行板コンデンサーに帯電していない厚さ$D$の導体板を挿入する.
極板A,Bの間隔を$d$,極板の面積を$S$,真空の誘電率を$\varepsilon_{0}$とすると,このコンデンサーの電気容量$C$は次のようになる.
$C=\varepsilon_{0}\dfrac{S}{d-D}$
これは,金属の厚さの分だけ,極板A,Bの間隔が縮まった考えることもできる.


コメント
[…] […]
[…] […]
[…] コンデンサーへの導体の挿入 […]