
平らな極板2枚を平行に固定してコンデンサーをつくりましょう.
もともと,極板には電荷が蓄えられていない状況で電池につなぐと,片方の極板からもう片方の極板に電荷が移動し,2枚の極板に電荷が蓄えられます.
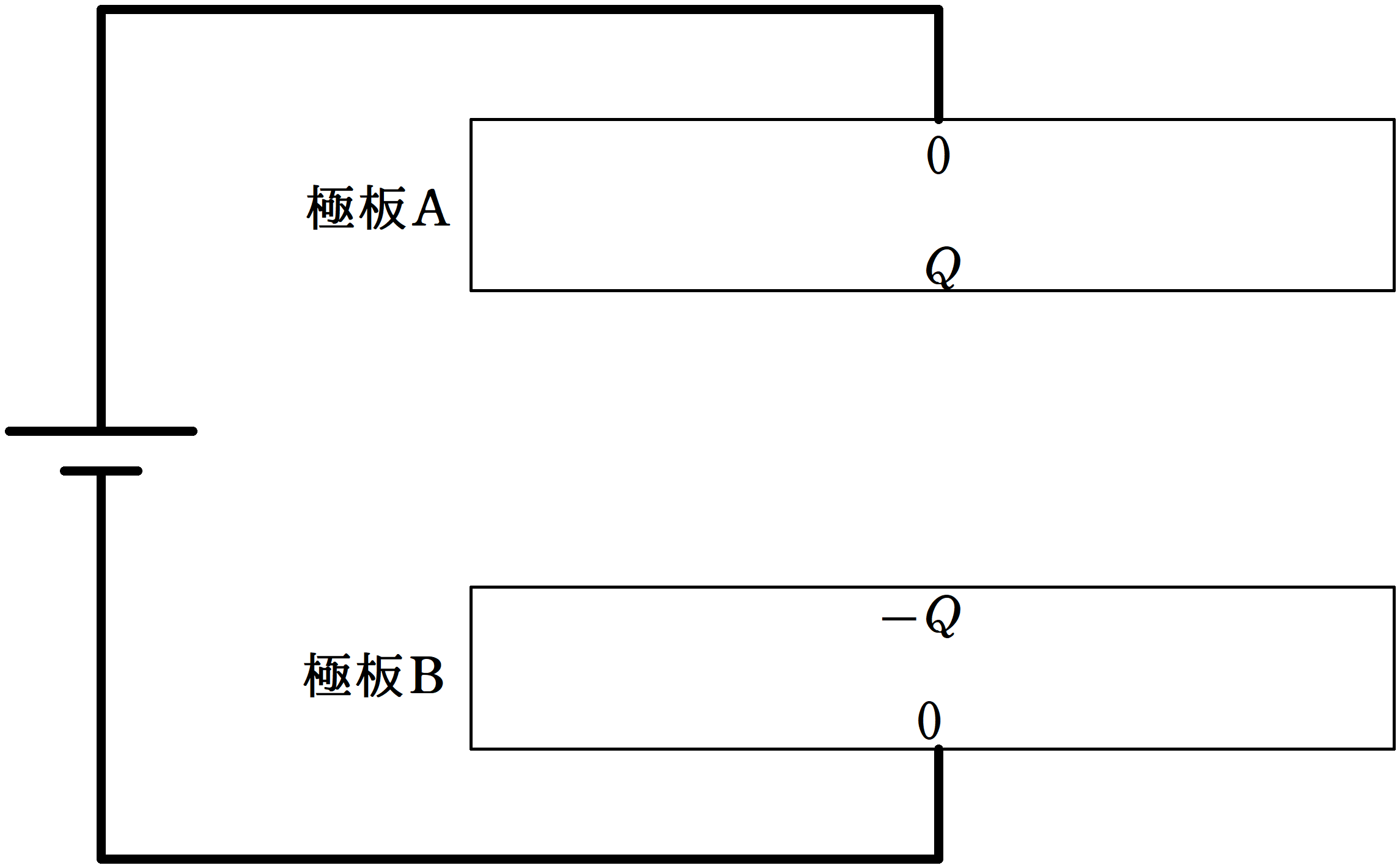
このとき,2枚の極板の電荷分布は,下のようにはなりません.
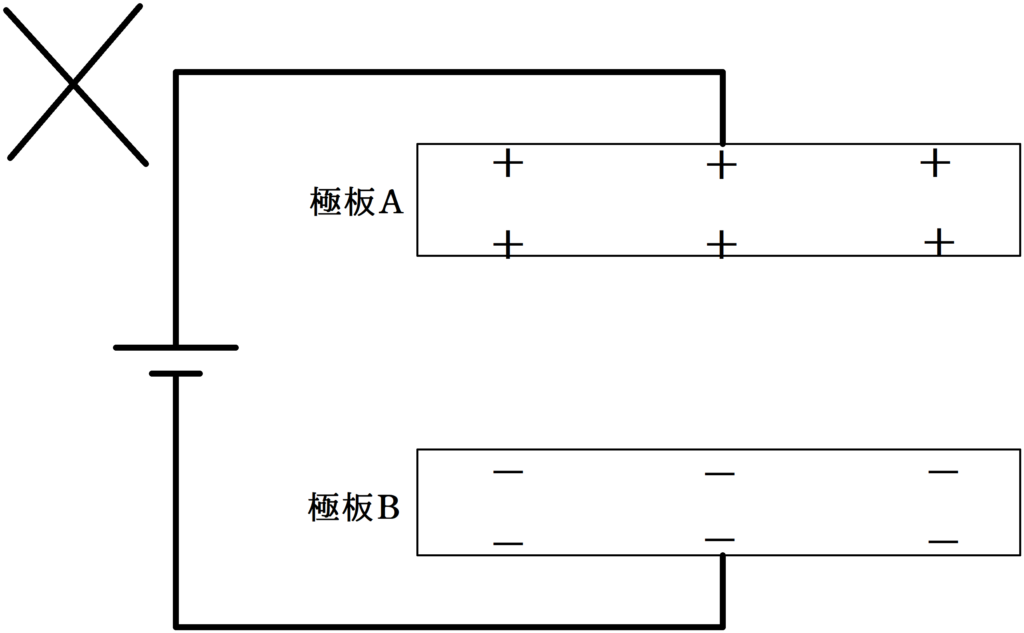

正しくは,次のように分布します.
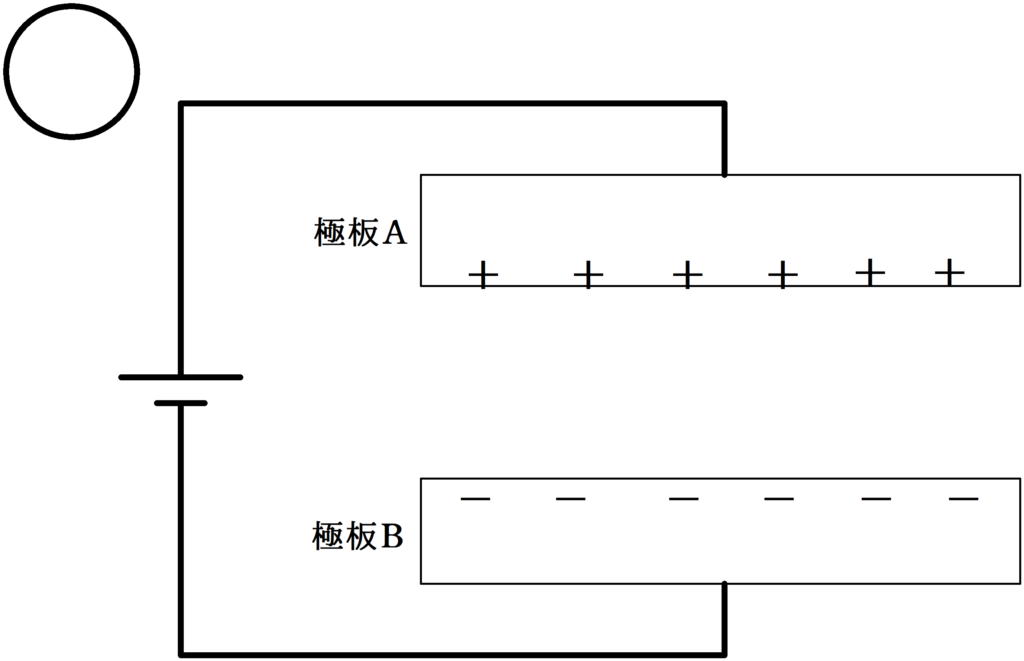

今回は,金属板の電荷分布が上のようになる理由について確かめていきたいと思います.
1.アースにつながっていない場合
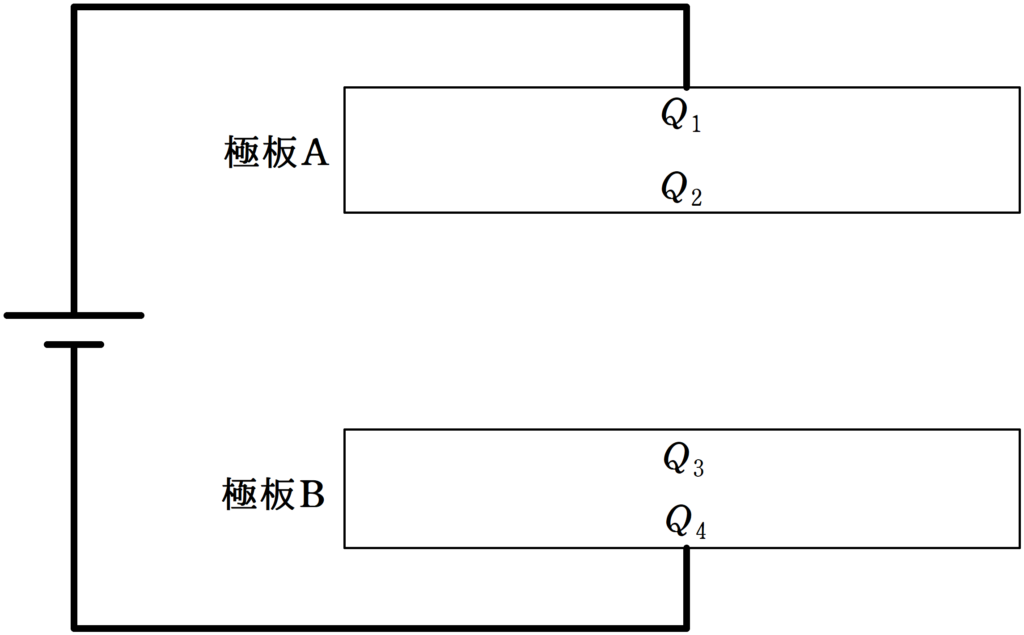

まず,設定です.
極板A,Bには電荷が蓄えられていないとしましょう.
極板A,Bを固定し,電源をつなぐと,電源を通して,極板間で電荷の移動が起こります.
また,アースがつながれていない状況を考え,そのため,極板に蓄えられた電荷の和は移動前と同じ0となります.(電荷保存則)
これと,極板A,Bが導体であることから導体内部の電場が0であることを考慮します.(静電誘導)
つまり,条件は次の3つです.
1.極板Aと極板Bに蓄えられた電荷の和は0
2.極板Aの内部の電場は0
3.極板Bの内部の電場は0
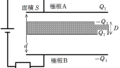
そして,電荷移動後の極板Aの上側に蓄えられている電荷を$Q_{1}$,下側に蓄えられている電荷を$Q_{2}$,極板Bの上側に蓄えれている電荷を$Q_{3}$,下側に蓄えれている電荷を$Q_{4}$とします.
とりあえずは,$Q_{1}$~$Q_{4}$をすべて正の電荷として考え,電場を計算していきます.
平面に分布された電荷がつくる電場は次のようになります.
十分に広い平面に一様な電荷$Q$が分布している.
真空の誘電率を$\varepsilon_{0}$,平面の面積を$S$とするとき,電場の大きさ$E$は
$E=\dfrac{|Q|}{2\varepsilon_{0}S}$
これは,電場が距離によらず一定であることを意味している.
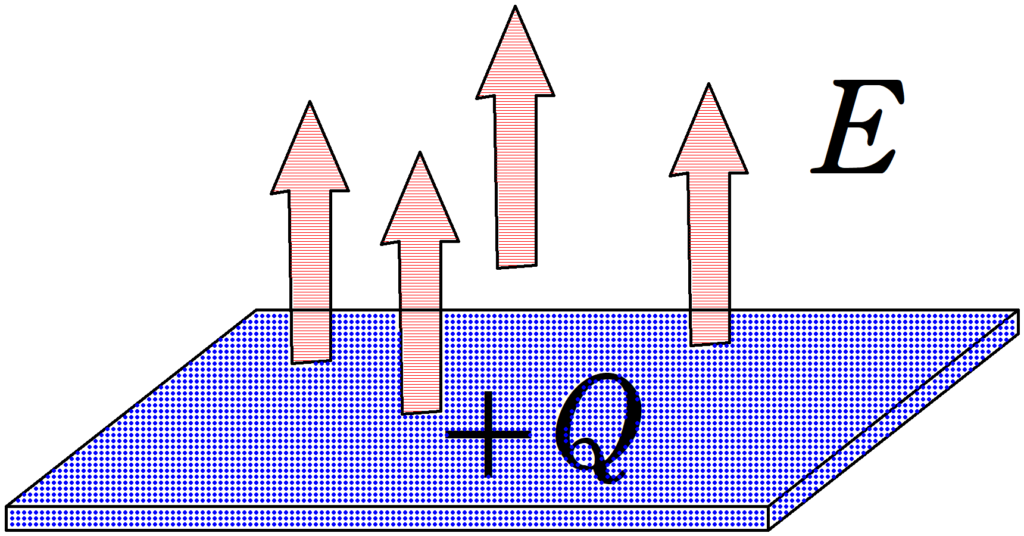

これらを考慮して,それぞれの電荷がつくる電場は次のようになります.
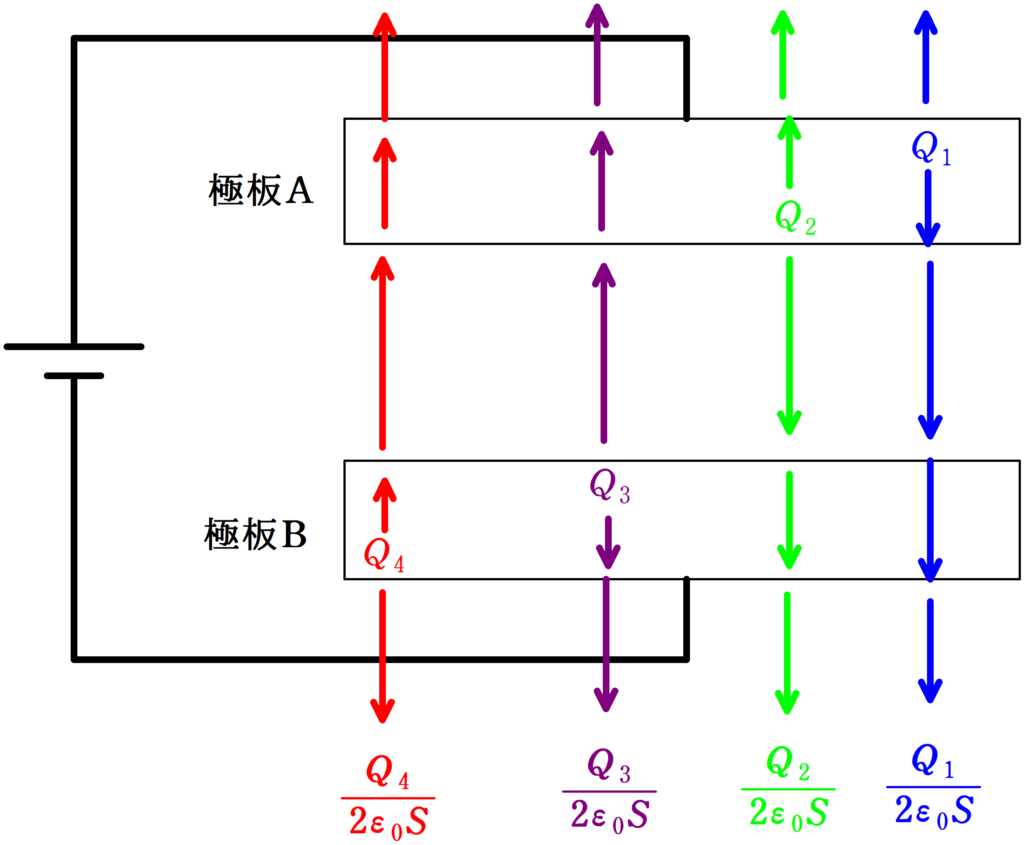

では3つの条件を考えましょう.
1.極板Aと極板Bに蓄えられた電荷の和は0
$Q_{1}+Q_{2}+Q_{3}+Q_{4}=0$ $\dots (\ast)$
2.極板Aの内部の電場は0
図の下向きを正として電場の重ね合わせを考えると
$\dfrac{Q_{1}}{2\varepsilon_{0}S}-\dfrac{Q_{2}}{2\varepsilon_{0}S}-\dfrac{Q_{3}}{2\varepsilon_{0}S}-\dfrac{Q_{4}}{2\varepsilon_{0}S}=0$
すなわち
$\dfrac{1}{2\varepsilon_{0}S}(Q_{1}-Q_{2}-Q_{3}-Q_{4})=0$
であるから
$Q_{1}-Q_{2}-Q_{3}-Q_{4}=0$ $\dots (2\ast)$
3.極板Bの内部の電場は0
図の下向きを正として電場の重ね合わせを考えると
$\dfrac{Q_{1}}{2\varepsilon_{0}S}+\dfrac{Q_{2}}{2\varepsilon_{0}S}+\dfrac{Q_{3}}{2\varepsilon_{0}S}-\dfrac{Q_{4}}{2\varepsilon_{0}S}=0$
すなわち
$Q_{1}+Q_{2}+Q_{3}-Q_{4}=0$ $\dots (3\ast)$
もう1度$(\ast)$~$(3\ast)$を並べると次のようになる.
$Q_{1}+Q_{2}+Q_{3}+Q_{4}=0$ $\dots (\ast)$
$Q_{1}-Q_{2}-Q_{3}-Q_{4}=0$ $\dots (2\ast)$
$Q_{1}+Q_{2}+Q_{3}-Q_{4}=0$ $\dots (3\ast)$

この$(\ast)$~$(3\ast)$を解けばいいんだね.
まずは,$(2\ast)+(3\ast)$を計算してみようかな.
★ $(2\ast)+(3\ast)$より
$2Q_{1}-2Q_{4}=0$ $\therefore Q_{1}=Q_{4}$

$Q_{1}=Q_{4}=Q^{\prime}$として,$(3\ast)$に代入してみましょう.
★ $Q_{1}=Q_{4}=Q^{\prime}$を$(3\ast)$に代入すると
$Q^{\prime}+Q_{2}+Q_{3}-Q^{\prime}=0$ $\therefore Q_{2}=-Q_{3}$

$Q_{2}=Q$とすると,$Q_{3}=-Q$というわけだね.
これと,$Q_{1}=Q_{4}=Q^{\prime}$を$(\ast)$に代入してみましょう.
★ $(\ast)$より
$Q^{\prime}+Q-Q+Q^{\prime}=0$ $\therefore Q^{\prime}=0$

なるほど,たしかに,$Q_{1}=Q_{4}=0$となったね.
そして,$Q_{2}=Q$,$Q_{3}=-Q$とすると,次のような電荷分布になるね.
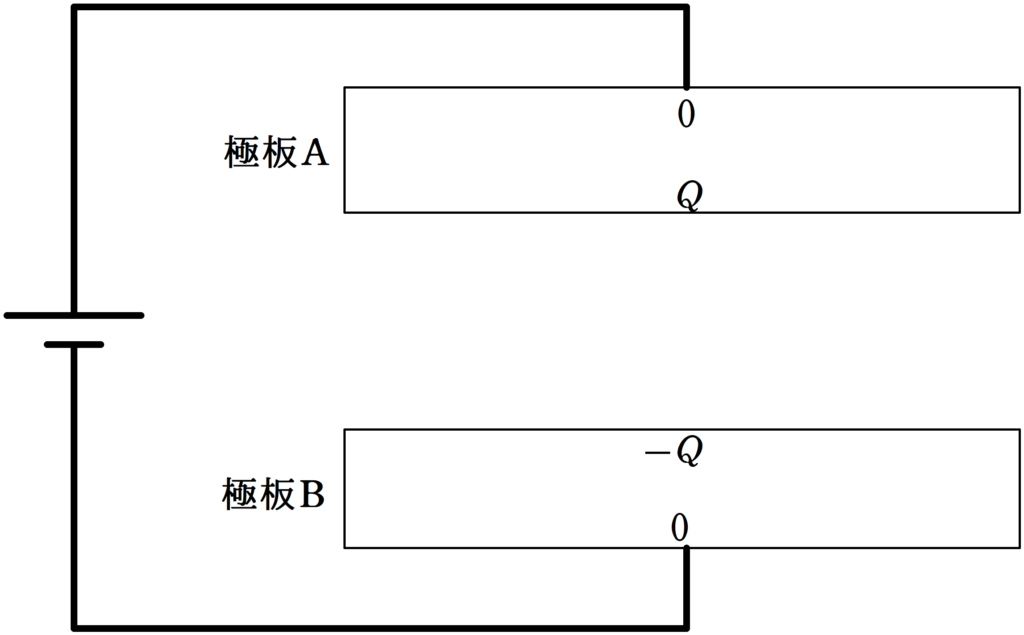
2.アースにつながっている場合
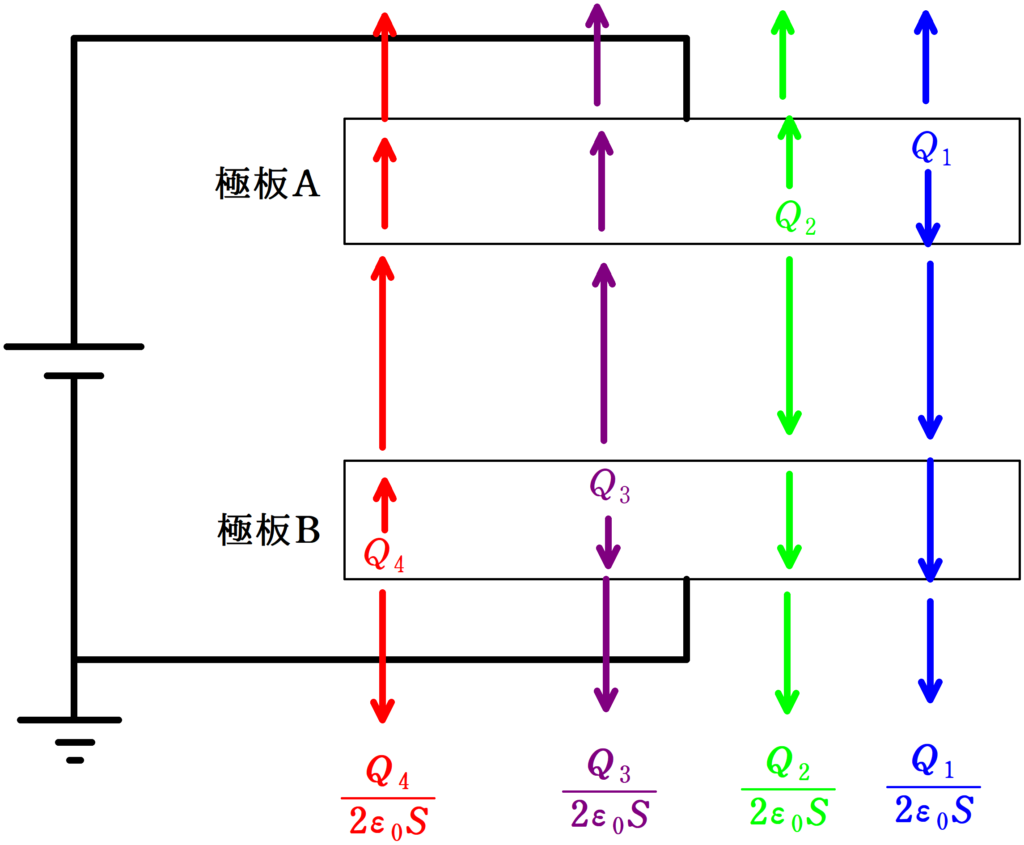

アースがつながっていたら,極板Aと極板Bの電荷が保存するとは限らないね.
どのように考えたらいいんだろう?

接地されていると,極板Bの下側と接地点との電位差はなくなってしまいます.
電位差がないので,電場が0です.
つまり,条件として,Bの下側部分の電場が0となります.
★ Bの下側部分の電場が0
$\dfrac{Q_{1}}{2\varepsilon_{0}S}+\dfrac{Q_{2}}{2\varepsilon_{0}S}+\dfrac{Q_{3}}{2\varepsilon_{0}S}+\dfrac{Q_{4}}{2\varepsilon_{0}S}=0$
したがって
$Q_{1}+Q_{2}+Q_{3}+Q_{4}=0$

これは,アースしていない場合の$(\ast)$の式と同じだね.
さらに,同じく極板AとBの内部の電場が0である条件を課せば,結局アースをつなげていないときの式と一致するから,結論も同じになるんだね.

はい.
というわけで,アースされていても,同じ電荷分布となります.
今回の電場の計算,電荷保存,導体内部の電場が0の条件式は,入試でも出てくるので,確認しておいてください.
また,これ以外の演習問題は下の記事で紹介しています.(大阪大の問題の一部です.)


コメント
[…] コンデンサーの極板の電荷分布PHYさん平らな極板2枚を平行に固定してコン… […]
[…] コンデンサーの極板の電荷分布 […]