弾性衝突とみなせる運動

PHYさん

一見，衝突にはみませんが，弾性衝突とみなすことができる問題があります．

今回は，この問題を扱ってみましょう．

問題1

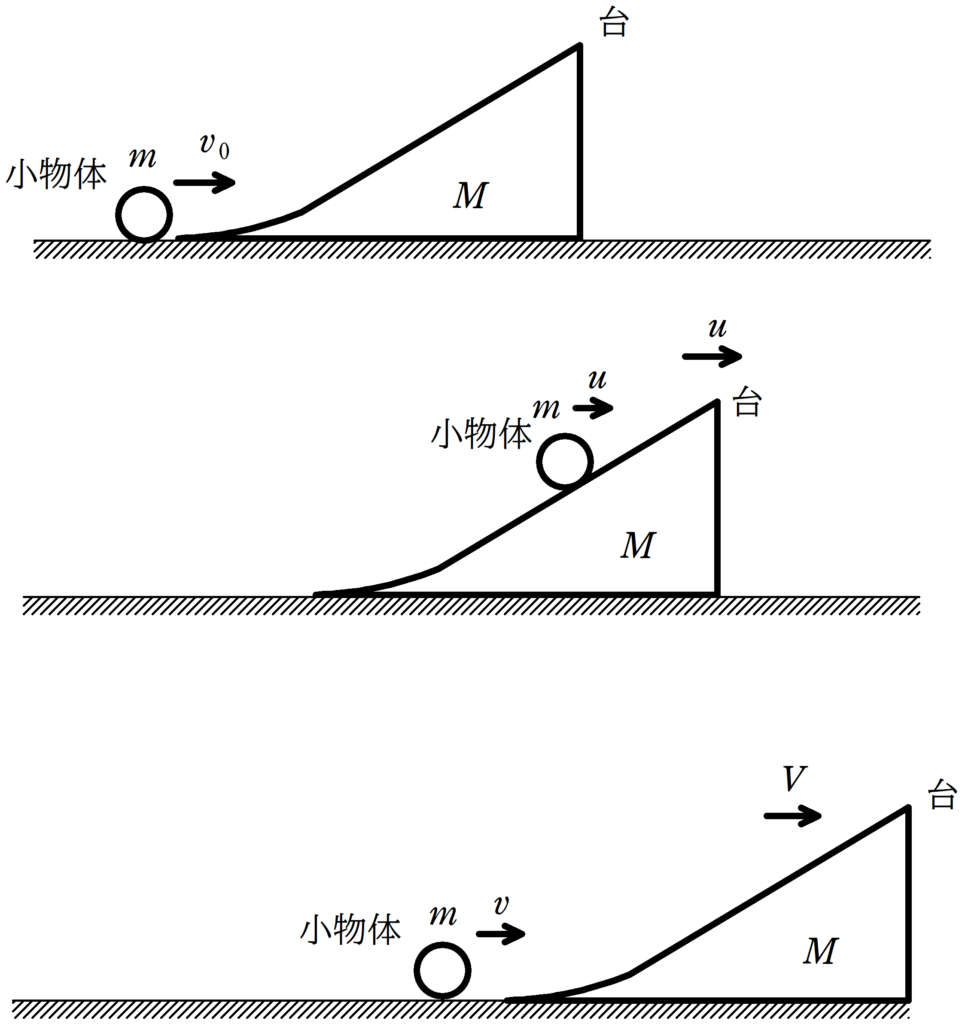
上図のように，なめらかな水平面になめらかな斜面をもつ質量$M$の台と質量$m$の小物体がある．

台を静止させて，小物体に初速度$v_{0}$を図の向きにあたえた．

しばらくすると，小物体は台の斜面に到達し，台も図の右方向へ動き出した．

小物体が斜面をのぼってもっとも高い位置に到達したときの小物体と台の速度を$u$とする．

その後，物体は斜面を下り，小物体は水平面に到達した．

このときの，小物体と台の速度をそれぞれ$v$，$V$とする．

(1)　$u$を$m$，$M$，$v_{0}$を用いて表せ．

(2)　$v$と$V$を$m$，$M$，$v_{0}$を用いて表せ．

＜解答＞

(1)

NEKO

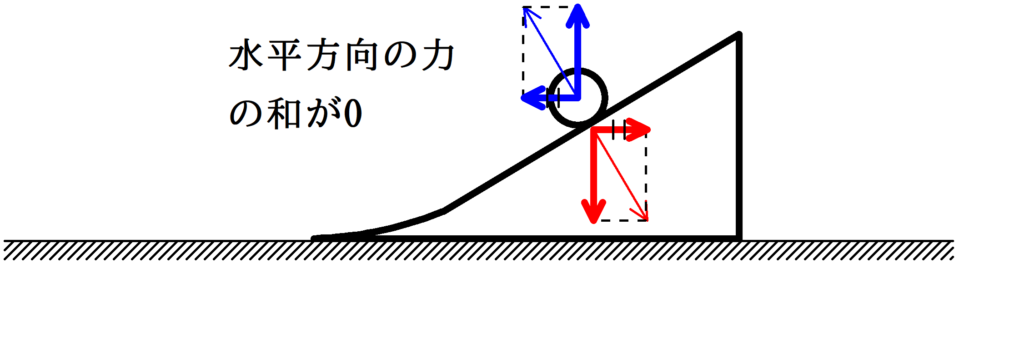
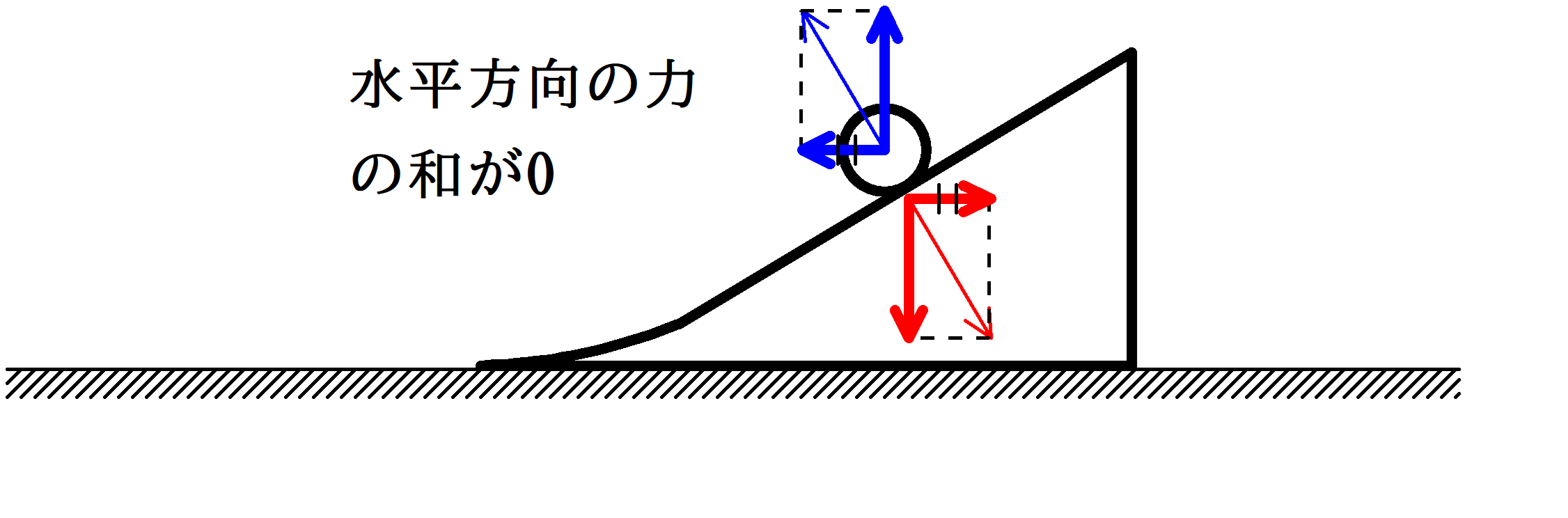
小物体が台の斜面をのぼっている間，小物体と台にはたらく水平方向の力の和は0です．

すると，運動量保存則が成り立ちます．

★　水平方向の運動量保存則

$mv_{0}+M\cdot 0=mu+Mu$　$\therefore$　$u=\dfrac{m}{M+m}v_{0}$

(2)

PHYさん

さて，小物体が離れた後の，小物体と台の速度を求めます．

同じく，運動量保存則が成り立ちますが，これだけでは2つの速度を求めることができません．

そこで，もう１つの式が必要になります．

力学的エネルギー保存則が成り立つので，力学的エネルギー保存則を立てます．

$mv_{0}+M\cdot 0=mv+MV$

$\dfrac{1}{2}mv_{0}^{2}+\dfrac{1}{2}M\cdot 0^{2}=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}MV^{2}$

この2式を解いてもいいのですが，やや大変です．

今回は台がもともと静止していたからよかったのですが，もともと動いているとさらに大変な式になります．

そこで，力学的エネルギー保存則が成り立つことを利用して，この運動のモデルを弾性衝突と考えてみましょう．

はねかえり係数の式

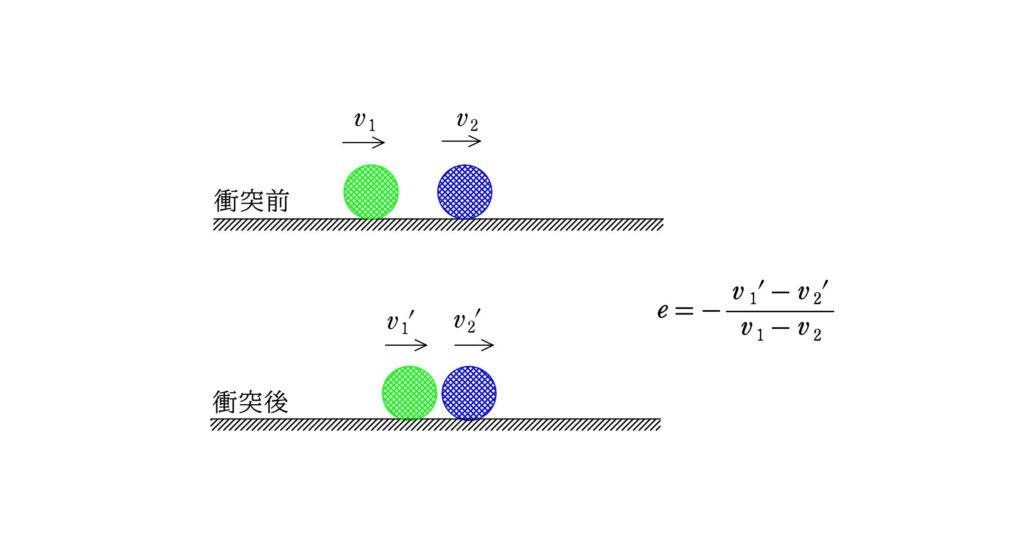
衝突前の物体の速度を$v_{1}$，$v_{2}$，衝突後の速度を$v_{1}^{\prime}$，$v_{2}^{\prime}$とするとき，はねかえり係数（反発係数）の式を次のように定義する．

$e=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$

$e=1$のときを弾性衝突といい，力学的エネルギーが保存する．

また，$e=0$のときを完全非弾性衝突という．

★　はねかえり係数の式

$1=-\dfrac{v-V}{v_{0}-0}$　$\dots　(\ast)$

★　運動量保存則

$mv_{0}+M\cdot 0=mv+MV$　$\dots　(2\ast)$

$(\ast)$を変形して

$v_{0}=-v+V$　

$\therefore$　$V=v_{0}+v$　$\dots　(3\ast)$

$(3\ast)$を$(2\ast)$に代入すると

$\eqalign{mv_{0}&=mv+M(v_{0}+v)\cr (M+m)v&=(m-M)v_{0}\cr v&=\dfrac{m-M}{M+m}v_{0}}$

さらに，この結果を$(3\ast)$に代入して

$\eqalign{V&=v_{0}+\dfrac{m-M}{M+m}v_{0}\\&=\dfrac{2m}{M+m}v_{0}}$

したがって，答えは$v=\dfrac{m-M}{M+m}v_{0}$，$V=\dfrac{2m}{M+m}v_{0}$