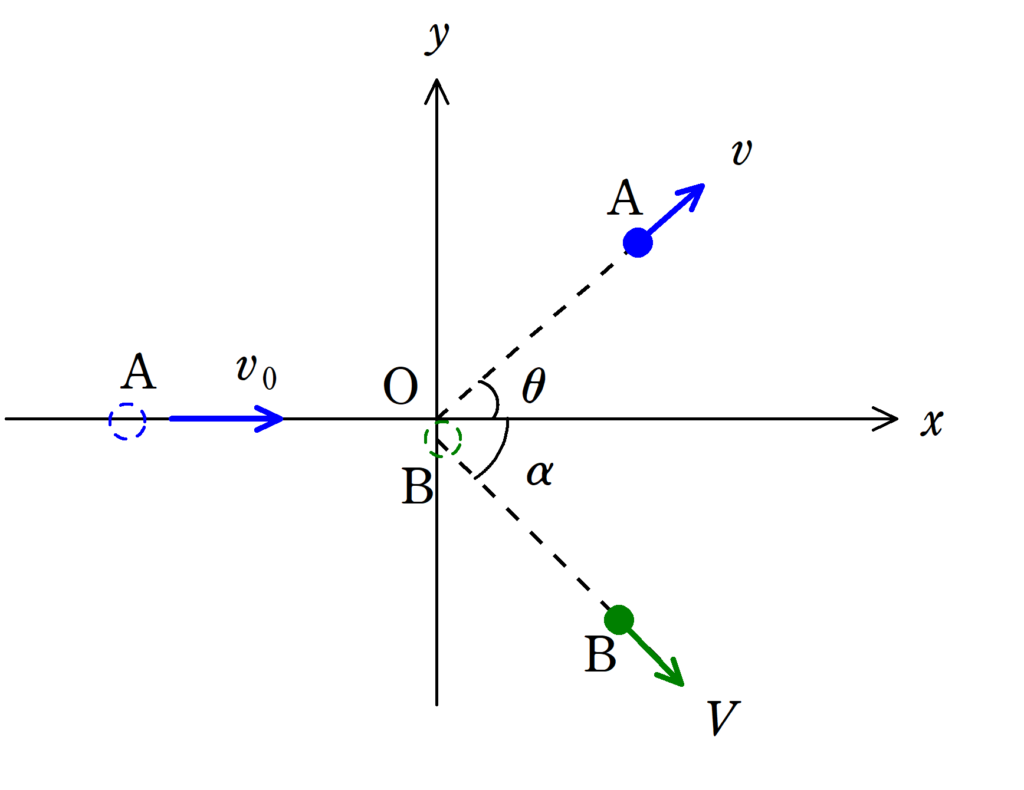
上図のようになめらかに動くことができる$xy$座標平面上の物体$\rm A$と物体$\rm B$の衝突を考える.質量$m$の物体$\rm A$は$x$軸の正の方向を速さ$v_{0}$で運動している.物体$\rm A$が原点で静止している質量$M$の物体$\rm B$に完全弾性衝突した後,物体$\rm A$は速さ$v(\neq 0)$で$x$軸から反時計回りに$\theta(0<\theta<\dfrac{\pi}{2})$の方向へ速度をもち,物体$\rm B$は速さ$V$で$x軸$から時計回りに$\alpha(0<\alpha<\dfrac{\pi}{2})$に速度をもった.このとき,次の問いに答えよ.
(1) 衝突直前後について,$x$方向,$y$方向それぞれについて,物体$\rm A$と$\rm B$を対象とした運動量保存則を立てよ.
(2) 衝突直前後について,物体$\rm A$と$\rm B$を対象とした力学的エネルギー保存則を立てよ.
(3) (1)(2)より,$v$を$M$,$m$,$v_{0}$,$\theta$から必要なものを用いて表せ.ただし,$M>m$とする.
<解答>

この問題は,立式自体が大変なのではなく,計算が大変です.
少し工夫をした解法を紹介しましょう.
(1)(2)
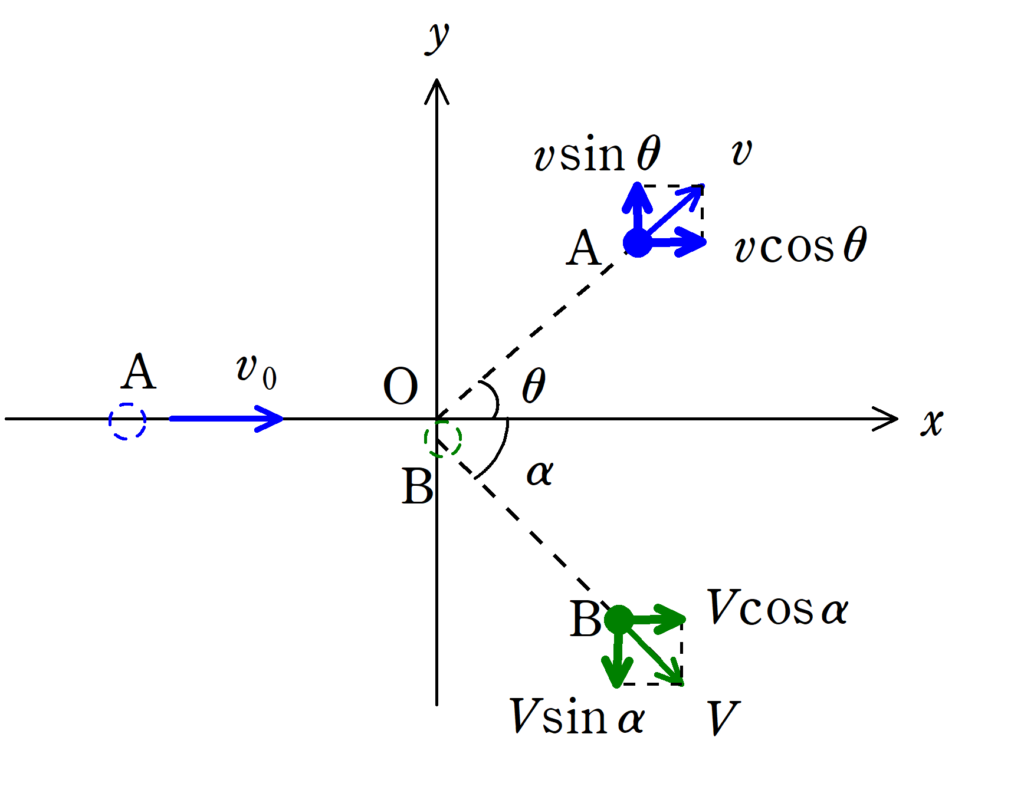
★ $x$方向の運動量保存則
$mv_{0}=mv\cos\theta +MV\cos\alpha$ $\dots (\ast)$(答)
★ $y$方向の運動量保存則
$0=mv\sin\theta -MV\sin\alpha$$\dots (2\ast)$ (答)
★ 力学的エネルギー保存則
$\dfrac{1}{2}mv_{0}^{2}=\dfrac{1}{2}mv^{2}+\dfrac{1}{2}MV^{2}$ $\dots (3\ast)$ (答)
(3)

$v$を$M$,$m$,$v_{0}$,$\theta$で表しなさい,と表現する文字が指定されていることから,$\alpha$を消去する必要があります.
$(\ast)$と$(2\ast)$から次のように変形して,$\sin^{2}\alpha +\cos^{2}\alpha =1$をを使って$\alpha$を消去します.
$MV\cos\alpha=m(v_{0}-v\cos\theta)$
$\therefore$ $(MV\cos\alpha)^{2}=m^{2}(v_{0}^{2}-2vv_{0}\cos\theta+v^{2}\cos^{2}\theta)$ $\dots (\ast)^{\prime}$
$MV\sin\alpha=mv\sin\theta$
$\therefore (MV\sin\alpha)^{2}=m^{2}v^{2}\sin^{2}\theta$ $\dots (2\ast)^{\prime}$

$(\ast)^{\prime}+(2\ast)^{\prime}$を計算します.
$\sin^{2}\alpha +\cos^{2}\alpha =1$と
$\sin^{2}\theta +\cos^{2}\theta =1$を利用します.
$M^{2}V^{2}(\cos^{2}\alpha +\sin^{2}\alpha)=m^{2}\{v_{0}^{2}-2vv_{0}\cos\theta+v^{2}(\cos^{2}\theta+\sin^{2}\theta)\}$
$\therefore$ $M^{2}V^{2}=m^{2}(v_{0}^{2}-2vv_{0}\cos\theta+v^{2})$ $\dots (\clubsuit)$

実は,この$(\clubsuit)$は次のようにも導出できます.
運動量保存則は,ベクトルの式です.
すなわち
衝突前の$\rm A$の運動量=衝突後の$\rm A$の運動量+衝突後の$\rm B$の運動量
が成り立ちます.すると,次のような三角形ができます.そこで,余弦定理を使います.
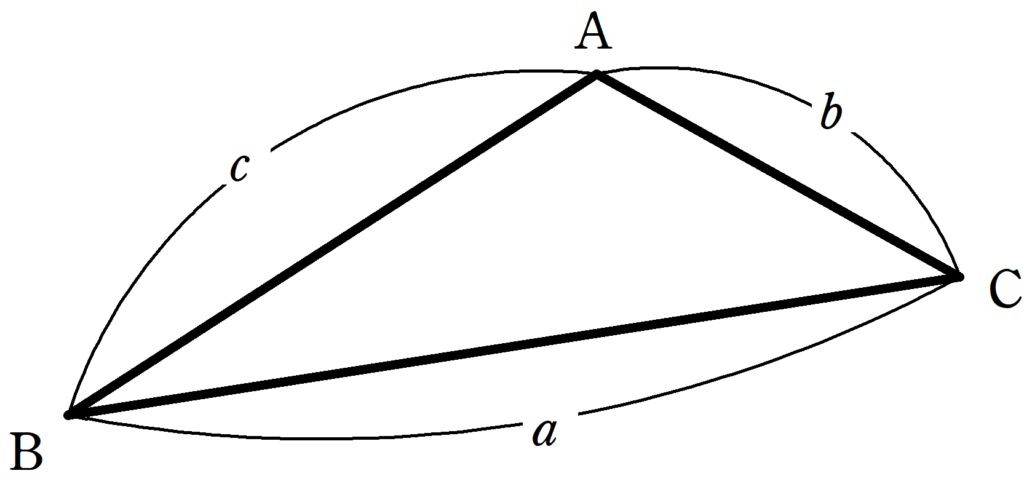
上の図のような三角形$\rm ABC$について,次の式が成り立つ.
$a^{2}=b^{2}+c^{2}-2bc\cdot \cos\angle{\rm A}$
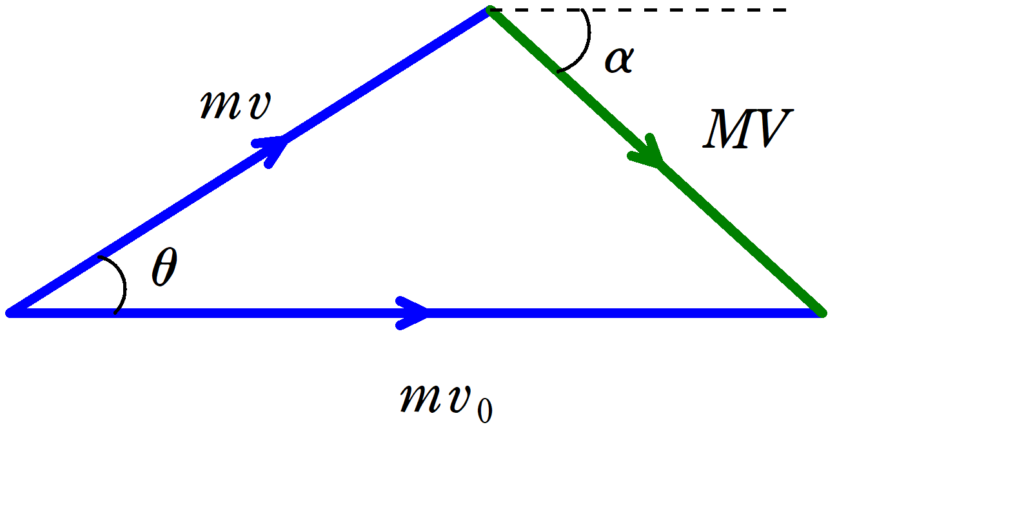
上の三角形について,余弦定理より
$(MV)^{2}=(mv)^{2}+(mv_{0})^{2}-2mv\cdot mv_{0}\cos\theta$
$\therefore$ $M^{2}V^{2}=m^{2}(v_{0}^{2}-2vv_{0}\cos\theta+v^{2})$ $\dots (\clubsuit)$

このように,かなり省略して$(\clubsuit)$を導出できます.
それでは,続きです.$(\clubsuit)$より
$V^{2}=\dfrac{m^{2}}{M^{2}}(v_{0}^{2}-2vv_{0}\cos\theta +v^{2})$ $(\clubsuit)^{\prime}$
を$(3\ast)$に代入します.
$(3\ast)$をあらかじめ両辺$\times 2$をして,$(\clubsuit)^{\prime}$を代入.
$\eqalign{\cancel{m}v_{0}^{2}&=\cancel{m}v^{2}+\cancel{M}\cdot \dfrac{m^{\cancel{2}}}{M^{\cancel{2}}}(v_{0}^{2}-2vv_{0}\cos\theta +v^{2})\cr Mv_{0}^{2}&=Mv^{2}+mv_{0}^{2}-2mvv_{0}\cos\theta +mv^{2}}$
$\therefore$ $(M+m)v^{2}-2mv_{0}\cos\theta\cdot v-(M-m)v_{0}^{2}=0$
$v$の2次方程式とみて,解の公式より
$\eqalign{v&=\dfrac{mv_{0}\cos\theta\pm\sqrt{m^{2}v_{0}^{2}\cos^{2}\theta+(M^{2}-m^{2})v_{0}^{2}}}{M+m}\\&=\dfrac{mv_{0}\cos\theta\pm v_{0}\sqrt{M^{2}-m^{2}(1-\cos^{2}\theta)}}{M+m}\\&=\dfrac{m\cos\theta\pm\sqrt{M^{2}-m^{2}\sin^{2}\theta}}{M+m}v_{0}}$

「$\pm$」になっているけど,どちらが答えなんだろう?

$m\cos\theta$と$\sqrt{M^{2}-m^{2}\sin^{2}\theta}$の大小を比較してみましょう.
2つとも2乗すると
$m^{2}\cos^{2}\theta$ と $M^{2}-m^{2}\sin^{2}\theta$
2つとも$m^{2}\sin\theta$を足して
$m^{2}(\sin^{2}\theta+\cos^{2}\theta)$ と$M^{2}$
すなわち
$m^{2}$と$M^{2}$
問題文の条件より,$m<M$なので,$m^{2}<M^{2}$.逆をたどっていけば,$m\cos\theta<\sqrt{M^{2}-m^{2}\sin^{2}\theta}$となります.
$v$は速さなので,$v>0$だから,結局
$v=\dfrac{m\cos\theta+\sqrt{M^{2}-m^{2}\sin^{2}\theta}}{M+m}v_{0}$ (答)

計算が大変だったね.また,「+」と「-」のどちらを選ぶかは慎重に計算しないとだね.



コメント