
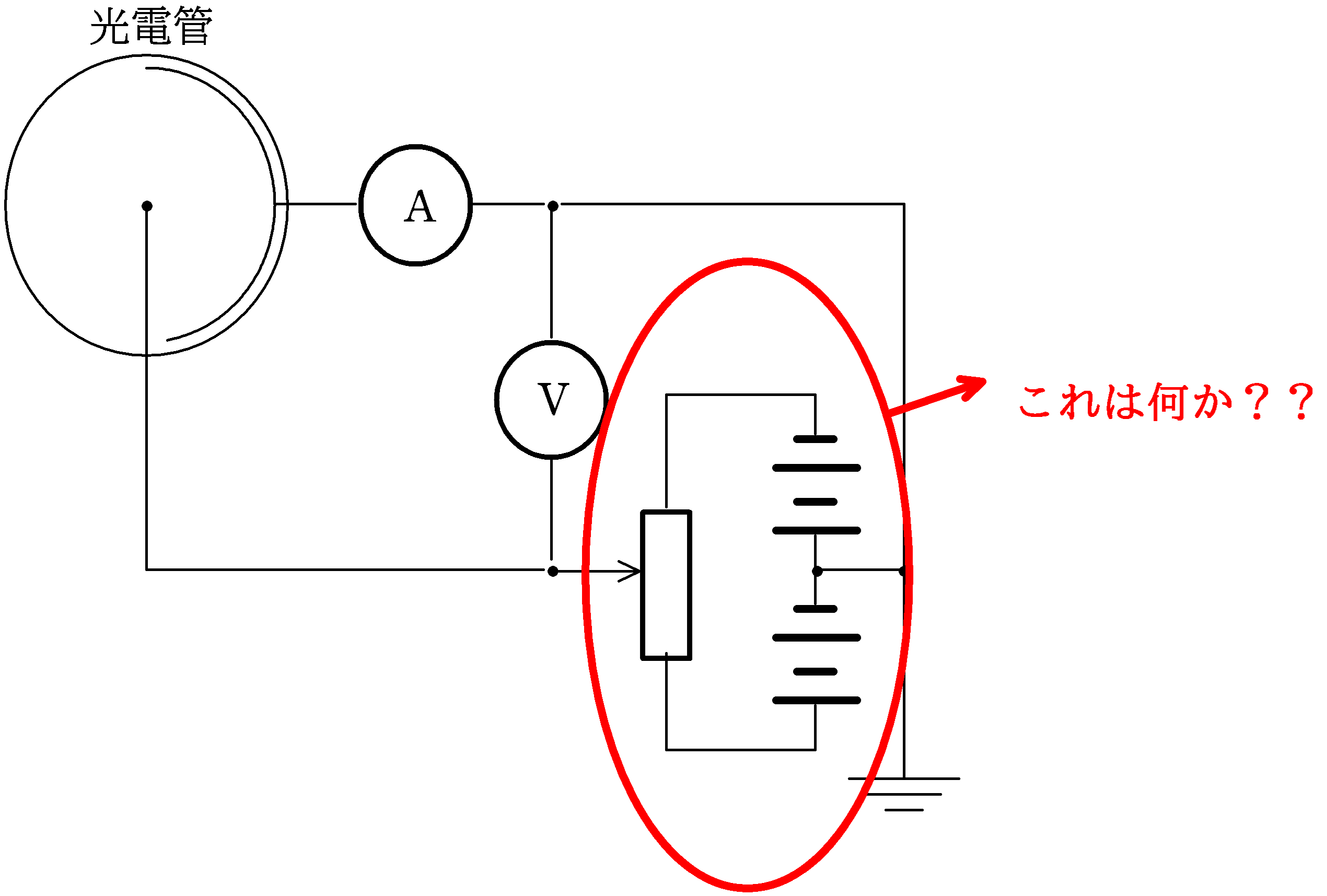
光電効果の実験でよく出てくる可変抵抗器っていったいどんな役割何なんだろう??
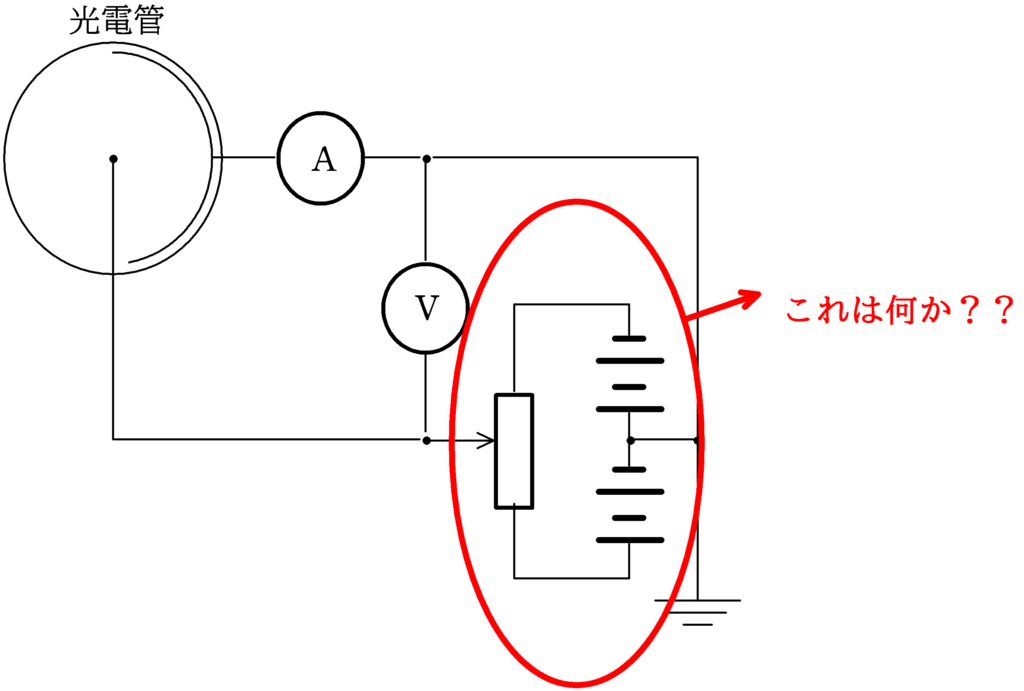

では,具体的に次のような設定をして,確認をしていきましょう.
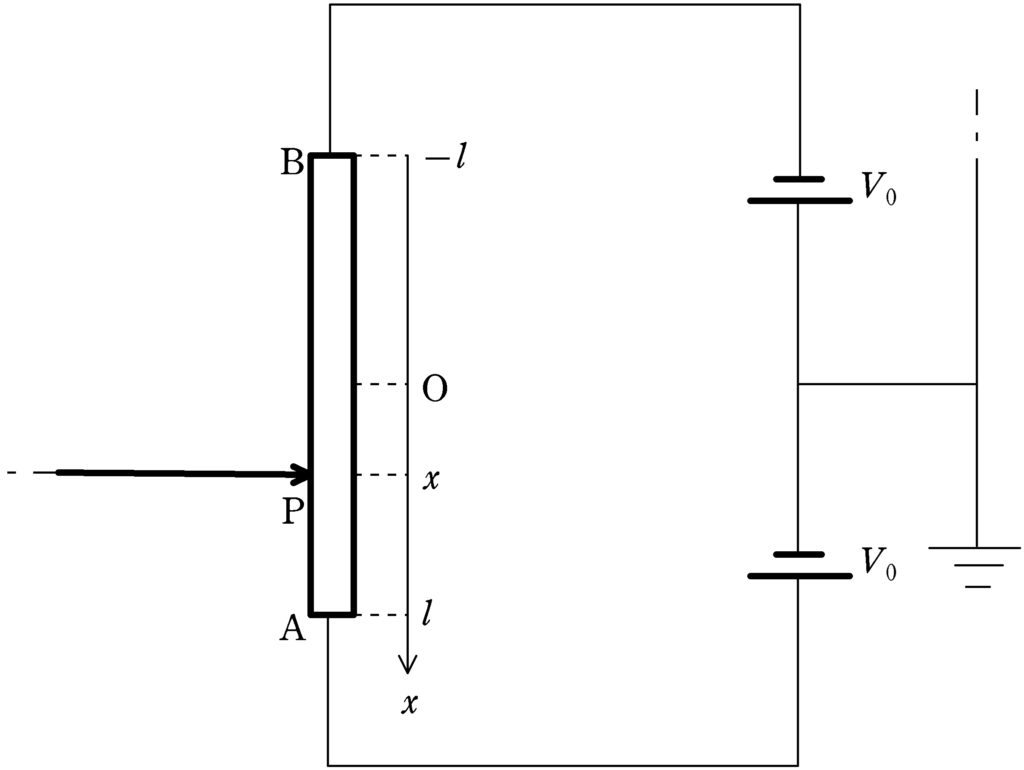

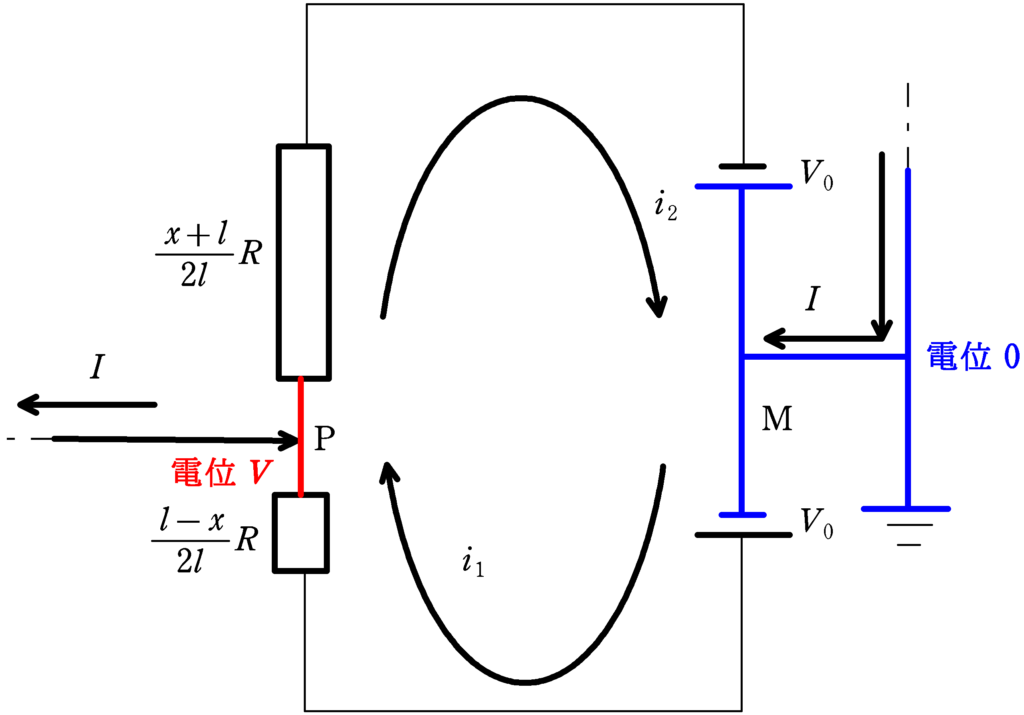
上は,2つの直流電池,アース,長さ$2l$で抵抗が$R$の可変抵抗を導線によって結んだ図です.
抵抗の中点を原点にとり,抵抗に沿って下向きに$x$軸をとります.Pが$x$のときの電位がどのようになるか考えます.
まず,抵抗は長さに比例することを確認しておきましょう.
長さ$l$,断面積$S$,抵抗率が$\rho$の電気抵抗の抵抗値$R$は
$R=\rho \dfrac{l}{S}$
※ 長い抵抗ほど,抵抗値が大きい.断面積が大きいと抵抗値は小さい.

図のAP間の抵抗を$R_{\rm AP}$,BP間の抵抗を$R_{\rm BP}$とします.AP間の長さが$l-x$,BP間の長さが$x+l$なので,次の比例式から$R_{\rm AP}$と$R_{\rm BP}$を求めることができます.
$R_{\rm AP}:R=(l-x):2l$ $\therefore\,\, R_{\rm AP}=\dfrac{l-x}{2l}R$
$R_{\rm BP}:R=(x+l):2l$ $\therefore\,\, R_{\rm BP}=\dfrac{x+l}{2l}R$
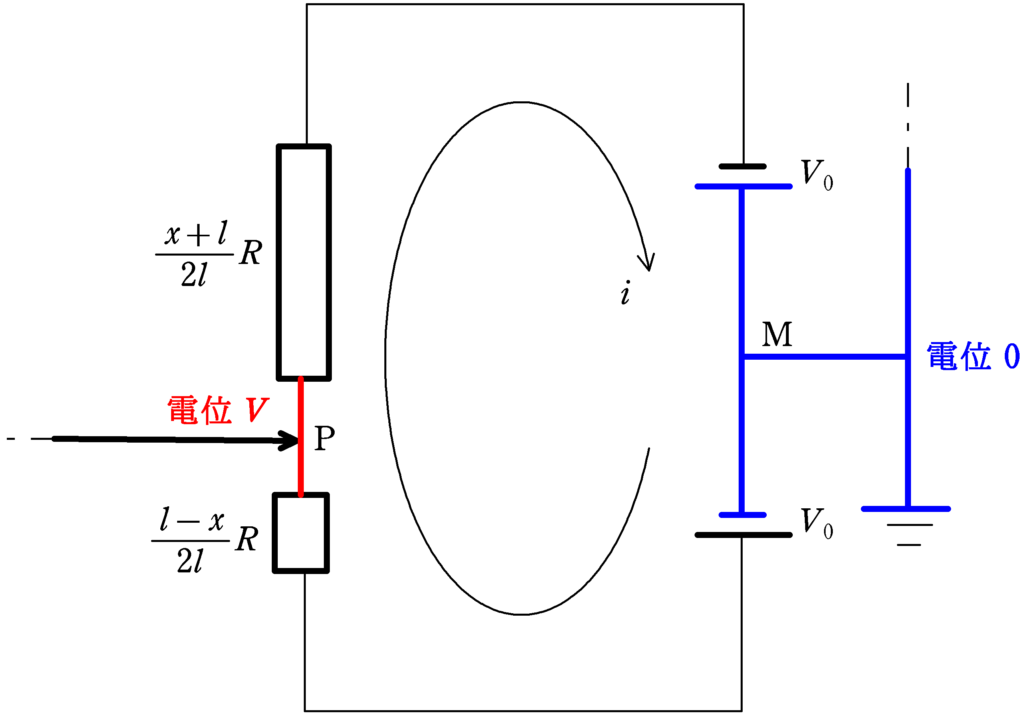

上図のように電流を設定して
①アースから矢印にそってPの位置まで電位を追う式(図のMからPまで)
と
②アースからスタートして矢印の向きに1周してアースにもどってくるような電位を追う式
を立ててみます.Pの電位を$V$とします.(図のM→P→M)
①MからPまでの電位を追う式
$0+V_{0}-\dfrac{l-x}{2l}Ri=V$ $\cdots (\ast)$
②M→P→Mの電位を追う式
$0+V_{0}-\dfrac{l-x}{2l}Ri-\dfrac{x+l}{2l}Ri+V_{0}=0$
$\therefore i=\dfrac{2V_{0}}{R}$ $\cdots (2\ast)$
$(2\ast)$を$(\ast)$を代入して
$\eqalign{V&=V_{0}-\dfrac{l-x}{\cancel{2}l}\bcancel{R}\times \dfrac{\cancel{2}V_{0}}{\bcancel{R}}\\&=V_{0}-\dfrac{l-x}{l}V_{0}=\dfrac{x}{l}V_{0}}$

$V=\dfrac{x}{l}V_{0}$ってことは,$-l\leqq x\leqq l$ まで移動させると,Pの電位は$-V_{0}\leqq V\leqq V_{0}$まで変化させることができるんだね.電位の正負まで調整できるんだ!

そうなります.

けど,もし下のように回路に電流が流れていたらこんなにきれいにならないんじゃない?
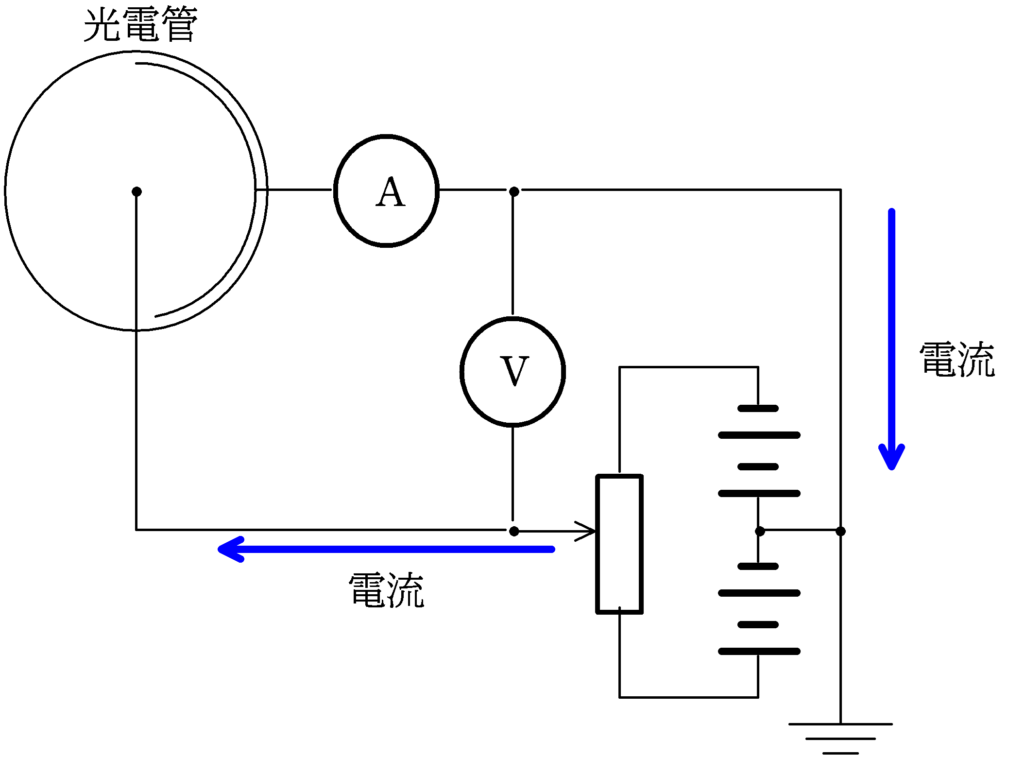

はい.もちろんPの電位は単純に$V=\dfrac{x}{l}V_{0}$とならず,外部の電流に依存する式が出てきます.
ただ,光電効果の実験は電流が流れる直後までを考えることが多いのと,もし上図のように外部に電流が流れても,抵抗$R$を小さくすることで,外部の電流の影響を小さくすることはできます.最後にもし外部に電流が流れたときにPの電位がどのようになるかを確認して終わりましょう.
電流を下図のように設定して
③キルヒホッフ第一法則
④MからPまでの電位を追う式
⑤M→P→Mの電位を追う式
を考えます.
③キルヒホッフ第一法則
$i_{2}+I=i_{1}$ つまり,$i_{2}=i_{1}-I$ $\cdots (3\ast)$
④MからPまでの電位を追う式
$0+V_{0}-\dfrac{l-x}{2l}Ri_{1}=V \cdots (4\ast)$
⑤M→P→Mの電位を追う式
$0+V_{0}-\dfrac{l-x}{2l}Ri_{1}-\dfrac{x+l}{2l}Ri_{2}+V_{0}=0$
$\therefore\,\, \dfrac{R}{2l}\times \left\{(l-x)i_{1}+(x+l)i_{2}\right\}=2V_{0}$
$\therefore\,\, (l-x)i_{1}+(x+l)i_{2}=\dfrac{4lV_{0}}{R}$
この式に$(3\ast)$を代入して,$i_{2}$を消去し$i_{1}$を求める.
$\eqalign{(l-x)i_{1}+(x+l)\times (i_{1}-I)&=\dfrac{4lV_{0}}{R}\\ 2li_{1}-(x+l)I&=\dfrac{4lV_{0}}{R}\\2li_{1}&=\dfrac{4lV_{0}}{R}+(x+l)I\\i_{1}&=\dfrac{2V_{0}}{R}+\dfrac{x+l}{2l}I}$
さらに,この式を$(4\ast)$に代入して$V$を求める.
$\eqalign{V&=V_{0}-\dfrac{l-x}{2l}R\left(\dfrac{2V_{0}}{R}+\dfrac{x+l}{2l}I\right)&=\dfrac{x}{l}V_{0}-\dfrac{l^{2}-x^{2}}{4l^{2}}RI}$

確かに$-\dfrac{l^{2}-x^{2}}{4l^{2}}RI$だけずれちゃうんだね.

入試ではここまで複雑な話はほとんどされません.
どちらかというと,$I=0$のとき,Pの電位は$V=\dfrac{x}{l}V_{0}$なので,PをOとAの間におけば,Pは正の電位,OとBの間におけばPは負の電位になるということです.ここはおさえておきましょう.


PをOAの間におくと,電圧降下が小さいから正の電位になり,PをOB間におくと電圧降下が大きくなるから負の電位になるんだね!

コメント