速度交換

PHYさん

今回は，速度交換についての話です．

次のことを確認しましょう．

一次元衝突についての証明

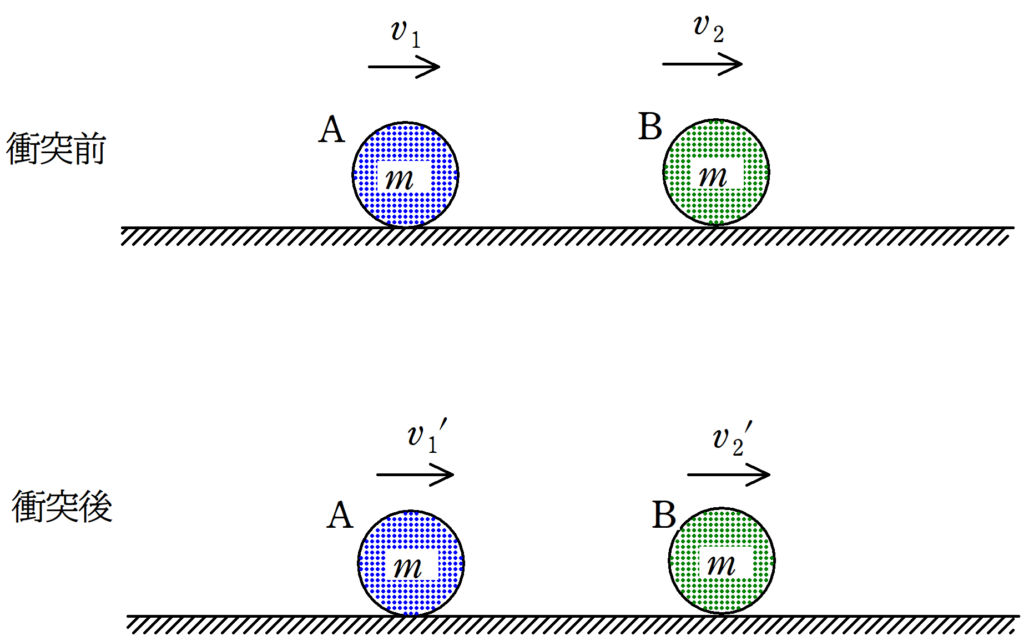
<設定>

質量$ｍ$の2つの物体A,Bの一次元衝突を考える．

A，Bの衝突前の速度をそれぞれ$v_{1}$，$v_{2}$とし，衝突後の速度をそれぞれ$v_{1}^{\prime}$，$v_{2}^{\prime}$とする．

★　運動量保存則

$mv_{1}+mv_{2}=mv_{1}^{\prime}+mv_{2}^{\prime}$　

$\therefore　v_{1}+v_{2}=v_{1}^{\prime}+v_{2}^{\prime}$　$\dots　(\ast)$

★　反発係数の式

$1=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$

$\therefore　v_{1}-v_{2}=-v_{1}^{\prime}+v_{2}^{\prime}$　$\dots　(2\ast)$

$(\ast)+(2\ast)$より

$2v_{1}=2v_{2}^{\prime}$

$\therefore$　$v_{2}^{\prime}=v_{1}$

$(\ast)-(2\ast)$より

$2v_{2}=2v_{1}^{\prime}$

$\therefore　v_{1}^{\prime}=v_{2}$

NEKO

確かに，速度が交換されているね．

二次元運動の衝突への応用

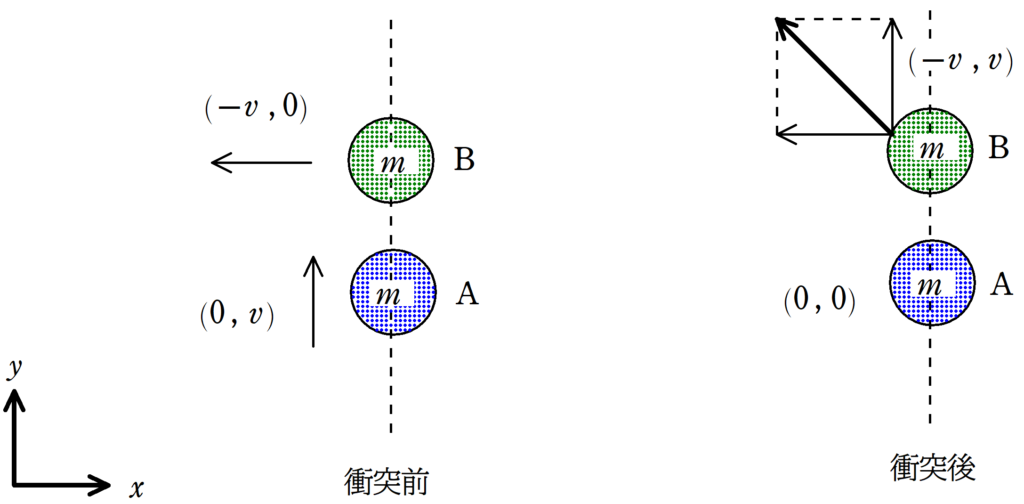
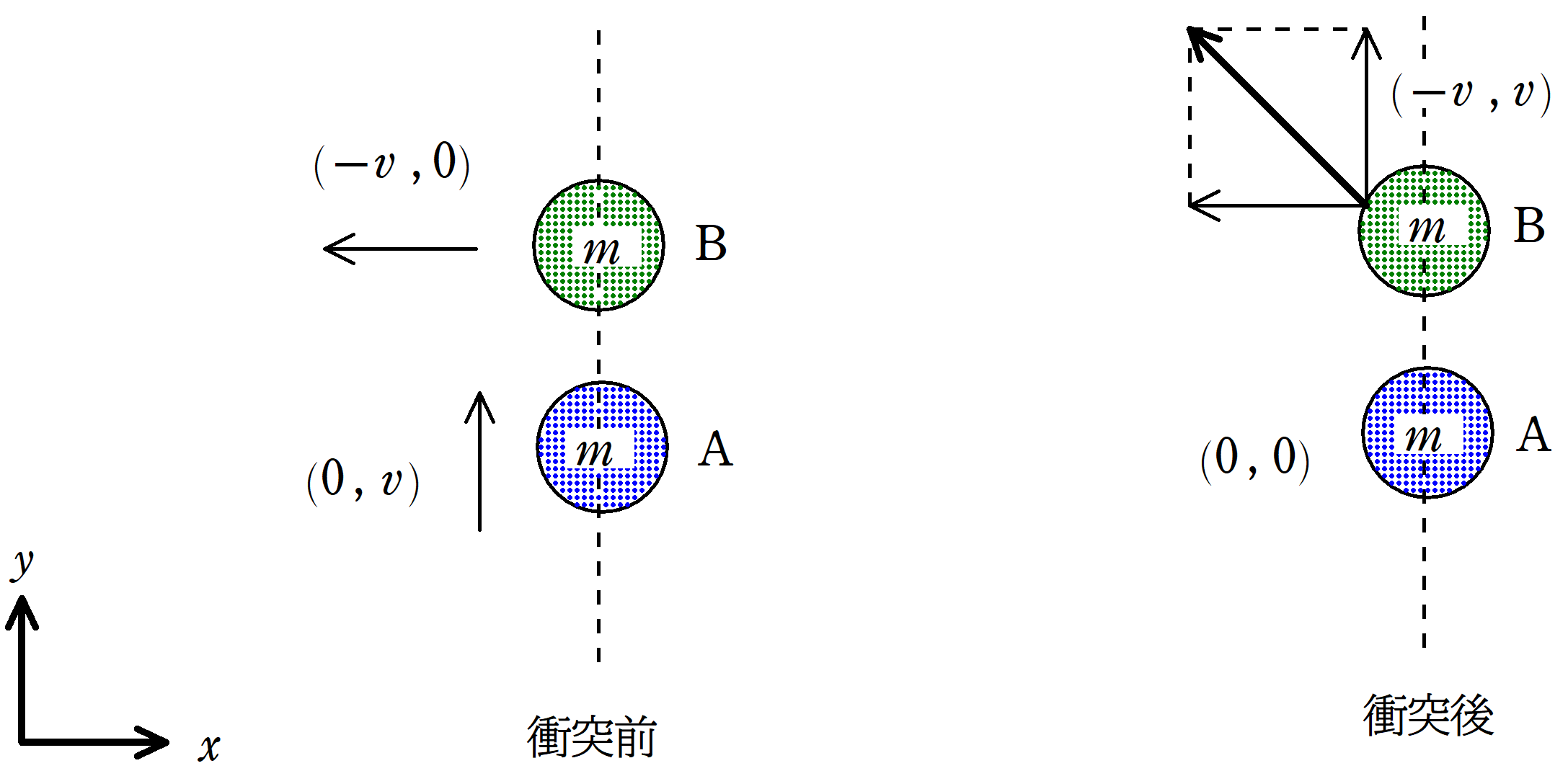
<設定>

質量が同じ物体AとBが水平面上で運動している．衝突前のAの速度が$v_{\rm A}=(0 , v)$，Ｂの速度が$v_{\rm B}=(-v , 0)$であった．衝突の瞬間はＡとＢの中心線が$y$軸に平行であった．

また，衝突の際のＡとＢの間の摩擦は無視する．

NEKO

ＡとＢの衝突後の$x$方向の速度は変化しないね．

一方，$y$軸方向の速度は速度が交換されるので，Aが$0$，Ｂの速度が$v$になり，Ｂは$(-v , v)$の速度になるんだね．