
今回は2021年の早稲田大理工の[1],熱力学の問題の熱効率の計算のみを扱います.
熱力学の基本公式はこちらでも紹介しています.
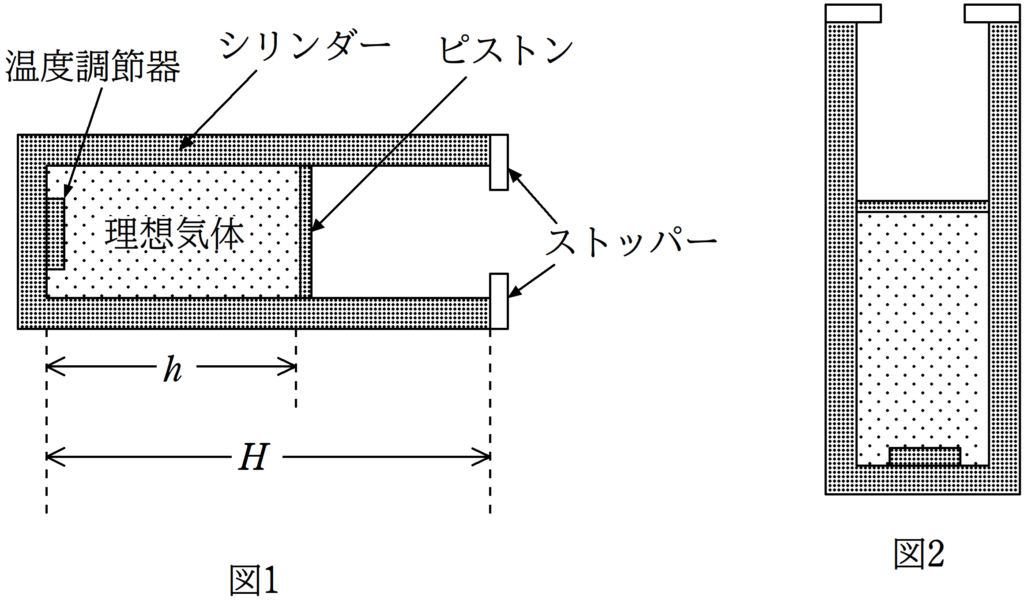
図1のように,理想気体が滑らかに動くピストンによってシリンダー内に封入されており,シリンダーは大気中に水平に置かれている.シリンダーの内部には温度調節器が設置され,理想気体を加熱したり冷却したりできる.シリンダーの開口部にはストッパーが取り付けられている.ピストンより外側の圧力は常に大気圧$p_{0}$である.シリンダーおよびピストンは断熱素材で作られており,ピストンの厚さおよび温度調節器の大きさは無視できるものとする.シリンダーの内側の長さを$H$,ピストンの面積を$S$,気体定数を$R$,この理想気体の定積モル比熱を$C_{v}$,重力加速度の大きさを$g$とする.
図1の状態において,シリンダーの閉じた端側からピストン面までの距離$h$は$h_{1}(<H)$であった.
この状態からシリンダーをゆっくりと鉛直に立てた(図2).この理想気体の圧力は$\alpha p_{0}$,距離$h$は$h_{2}$となった.
続けて,図2の状態から温度調節器を用いて理想気体をゆっくりと温めたところ,この加熱によって距離$h$は$h_{3}(<H)$となった.
ここからさらに,シリンダーをゆっくりと水平に戻したところ,距離$h$は$h_{4}(<H)$になった.
最後に温度調節器を用いて理想気体をゆっくりと冷やし,距離$h$を$h_{1}$に戻した.
このシリンダーの直立,加熱,横倒し,冷却の一連のサイクルにおいて,ピストンがストッパーに触れることはなかった.このとき,次の問いに答えよ.
(1) このサイクルの熱効率$e$を$h_{1}$,$h_{2}$,$h_{3}$,$h_{4}$,$\alpha$を用いて表せ.
(2) このサイクルにおける断熱過程では,理想気体の圧力$p$と体積$V$の間に,$pV^{\gamma}=$一定の関係(ポアソンの法則)が成り立つ.$\gamma$は定数である.このことから,このサイクルにおける熱効率$e$を$\alpha$と$\gamma$を用いて表せ.
<解答>
(1)

距離が$h_{1}$,$h_{2}$,$h_{3}$,$h_{4}$の状態をそれぞれ状態①,②,③,④と名付けましょう.
それぞれの状態は次のように変化しています.
状態①→②:断熱圧縮(断熱材でできている+温度調節器を作動させていない.)
状態②→③:定圧膨張(ピストンにはたらく力の情報が変化していない.)
状態③→④:断熱膨張(断熱材でできている+温度調節器を作動させていない.)
状態④→①:定圧圧縮(ピストンにはたらく力の情報が変化していない.)
熱力学の問題に慣れていれば,どのような変化をしているかは,簡単に見極められるでしょう.
縦軸が圧力$p$,横軸が体積$V$とした$pV$図をえがくと次のようになります.
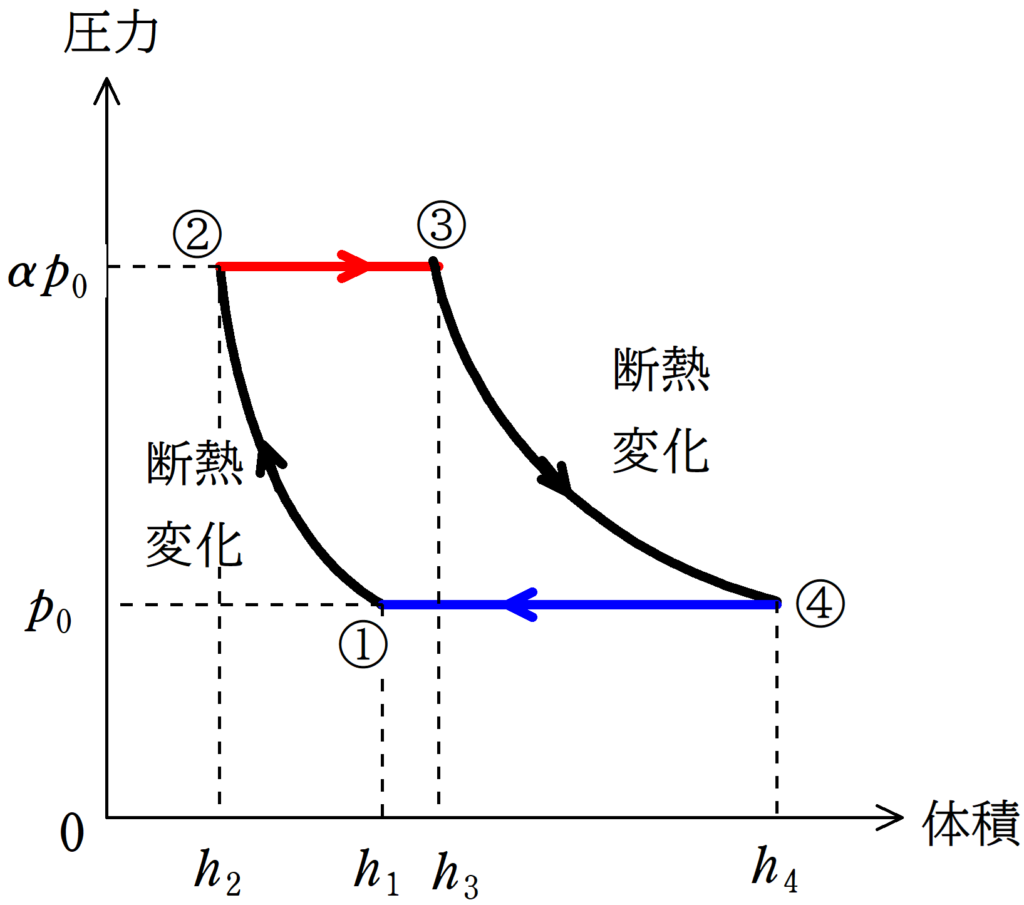

熱効率$e$を計算するときに,せっかく①→②と③→④が断熱変化なので,仕事を計算するのではなく,熱量だけの式で計算しましょう.
吸収した熱量を$Q_{\rm{in}}$,放出した熱量を$Q_{\rm_{out}}$,気体が正味のした仕事(気体がした正の仕事,負の仕事を符号付きですべて足すこと)を$W_{気体}$とすると,熱効率$e$は
$e=\dfrac{W_{気体}}{Q_{\rm{in}}}=\dfrac{Q_{\rm{in}}-Q_{\rm{out}}}{Q_{\rm{in}}}=1-\dfrac{Q_{\rm{out}}}{Q_{\rm{in}}}$

②→③が吸熱過程,④→①が放熱過程だね.
それぞれの熱量を$Q_{23}$,$Q_{41}$とします.
まずは,$Q_{23}$からいきましょう.
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$
物質量$n$,絶対温度$T$の内部エネルギーUは,定積モル比熱$C_{V}$を用いて
$U=nC_{V}T$
と表す.このとき,$C_{V}$は比例定数であって,定積変化以外でも上の式は成り立つ.

今回は温度変化$\varDelta T$ではなく,体積$Sh$の方を使いたいので,あらかじめ内部エネルギーの式を変形しておきましょう.
$\varDelta U=nC_{v}\varDelta T$ $\dots (\ast)$
また,理想気体の状態方程式$pV=nRT$について,
$nT=\dfrac{pV}{R}$
より,圧力一定のとき
$n\varDelta T=\dfrac{p\varDelta V}{R}$ $\dots (2\ast)$
$(2\ast)$を$(\ast)$に代入すると
$\eqalign{\varDelta U&=nC_{v}\varDelta T\\&=C_{v}\dfrac{p\varDelta V}{R}\\&=C_{v}\dfrac{pS\varDelta h}{R}}$
★ 状態②→③の熱力学第一法則
$\eqalign{Q_{23}&=\varDelta U_{23}+W_{23}\\&=C_{v}\dfrac{\alpha pS(h_{3}-h_{2})}{R}+\alpha pS(h_{3}-h_{2})\\&=\dfrac{\alpha pS(C_{v}+R)(h_{3}-h_{2})}{R}}$
★ 状態④→①の熱力学第一法則
$\eqalign{Q_{41}&=\varDelta U_{41}+W_{41}\\&=C_{v}\dfrac{pS(h_{1}-h_{4})}{R}+pS(h_{1}-h_{4})\\&=-\dfrac{pS(C_{v}+R)(h_{4}-h_{1})}{R}}$
★ 熱効率
$\eqalign{e&=\dfrac{Q_{23}+Q_{41}}{Q_{23}}\\&=1+\dfrac{Q_{41}}{Q_{23}}\\&=1+\dfrac{-\dfrac{pS(C_{v}+R)(h_{4}-h_{1})}{R}}{\dfrac{\alpha pS(C_{v}+R)(h_{3}-h_{2})}{R}}\\&=1-\dfrac{h_{4}-h_{1}}{\alpha (h_{3}-h_{2})}}$
したがって,答は$e=1-\dfrac{h_{4}-h_{1}}{\alpha (h_{3}-h_{2})}$
(2)

状態①→②,および状態③→④は断熱変化なので,ポアソンの式を立てることができます.
★ ポアソンの式
状態①→②について
$p(Sh_{1})^{\gamma}=\alpha p(Sh_{2})^{\gamma}$
$h_{1}=\alpha^{\frac{1}{\gamma}}h_{2}$ $\dots (3\ast)$
状態③→④について
$p(Sh_{4})^{\gamma}=\alpha p(Sh_{3})^{\gamma}$
$h_{4}=\alpha^{\frac{1}{\gamma}}h_{3}$ $\dots (4\ast)$

$(3\ast)$と$(4\ast)$を(1)で得た熱効率$e$の式に代入しましょう.
$\eqalign{e&=1-\dfrac{h_{4}-h_{1}}{\alpha (h_{3}-h_{2})}\\&=1-\dfrac{\alpha^{\frac{1}{\gamma}}h_{3}-\alpha^{\frac{1}{\gamma}}h_{2}}{\alpha (h_{3}-h_{2})}\\&=1-\alpha^{\frac{1}{\gamma}-1}\\&=1-\alpha^{\frac{1-\gamma}{\gamma}}}$
したがって,答は,$e=1-\alpha^{\frac{1-\gamma}{\gamma}}$



コメント