
オームの法則が成り立たないような電球やダイオードが回路にある場合,特性曲線という電流と電圧の関係のグラフが与えられるよね.
その場合,特性をもつ素子(電球やダイオード)の電圧を$V$,流れる電流を$I$として,キルヒホッフの法則を立てて,その式を特性曲線のグラフに書き込んでグラフの交点を求めるけど,なぜ交点を求めると答えが出るんだろう??

それでは,理由を考える前に次の例題を考えてみましょう.
まずは,例題から
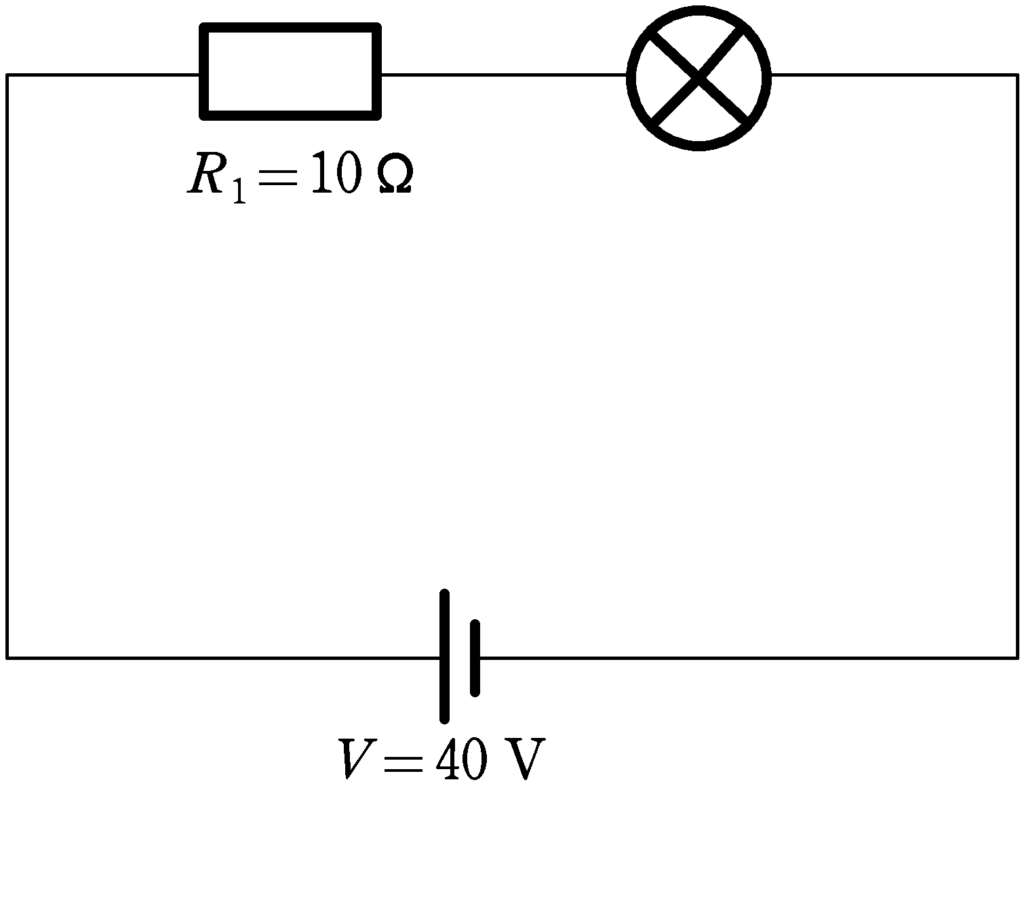
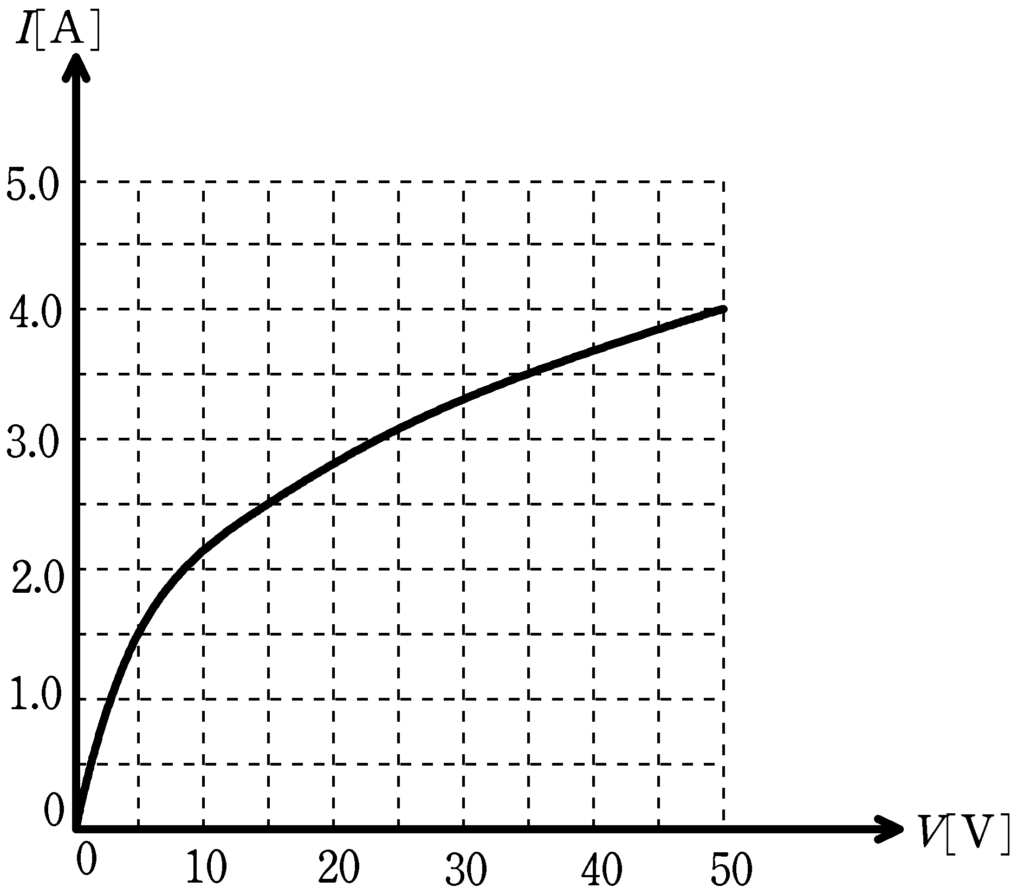
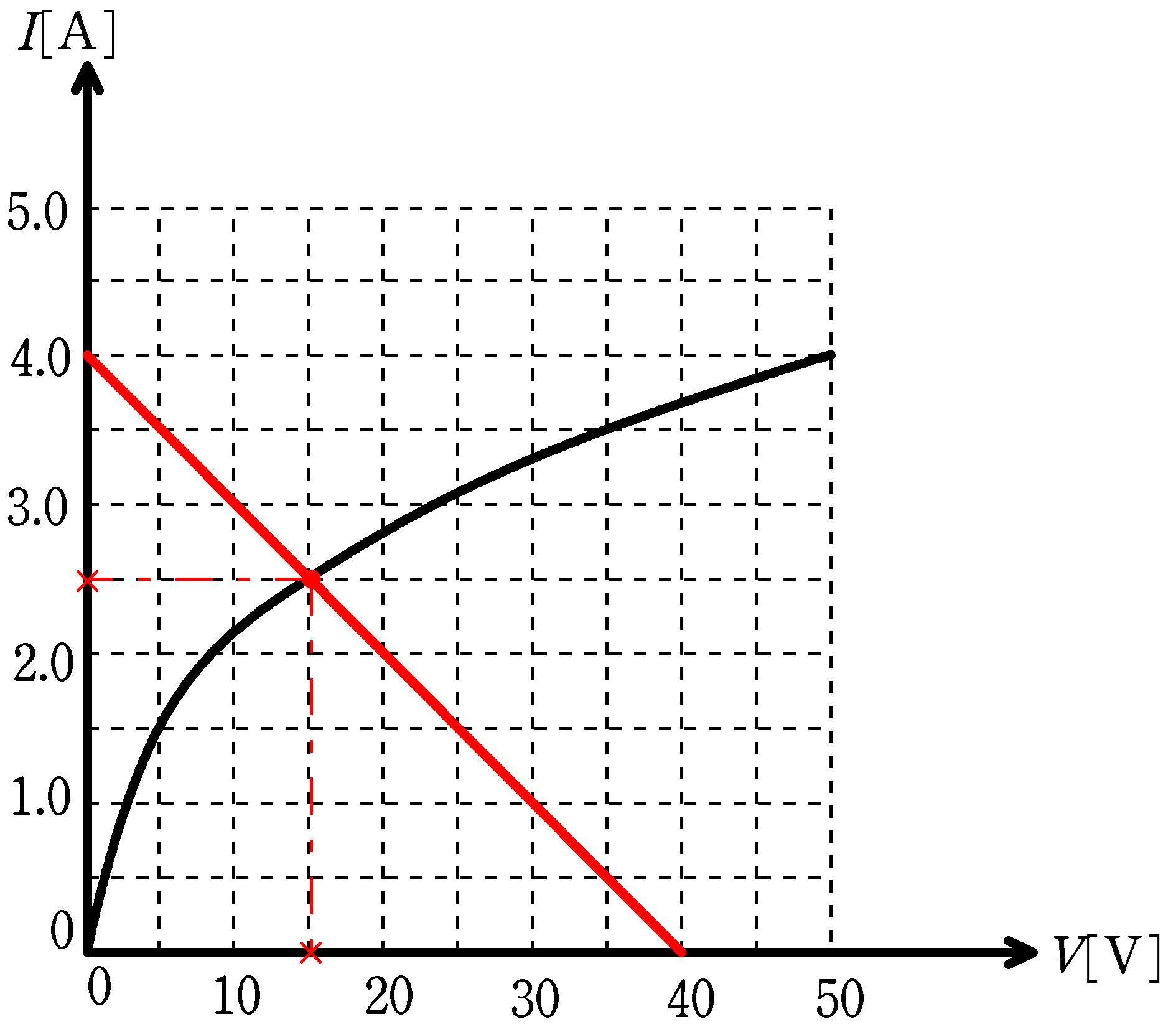
上図(上)のように,起電力$40\rm V$の内部抵抗の無視できる直流電源,抵抗値$10 \Omega$の抵抗が抵抗の無視できる導線で結ばれている.電球を流れる電流とかかる電圧の関係は上図(下)の曲線で表される.たとえば,電球に$1.5 \rm A$の電流が流れるときにかかる電圧は$5.0 \rm V$であり,$4.0 \rm A$の電流が流れるときにかかる電圧は$50 \rm V$である.
このとき,上図(上)の回路に流れる電流の大きさ(A)と,電球にかかる電圧(V)をそれぞれ求めよ.
<答え>
電球に流れる電流を$I[\rm A]$,かかる電圧を$V[\rm V]$とおく.このとき,$10 \Omega$の抵抗に流れる電流も$I[\rm A]$であるから,キルヒホッフ第2法則より
$40-10\cdot I-V=0$
$\therefore I=4.0-\dfrac{V}{10}$
この直線の式を特性曲線のグラフに書き込み,交点を調べると
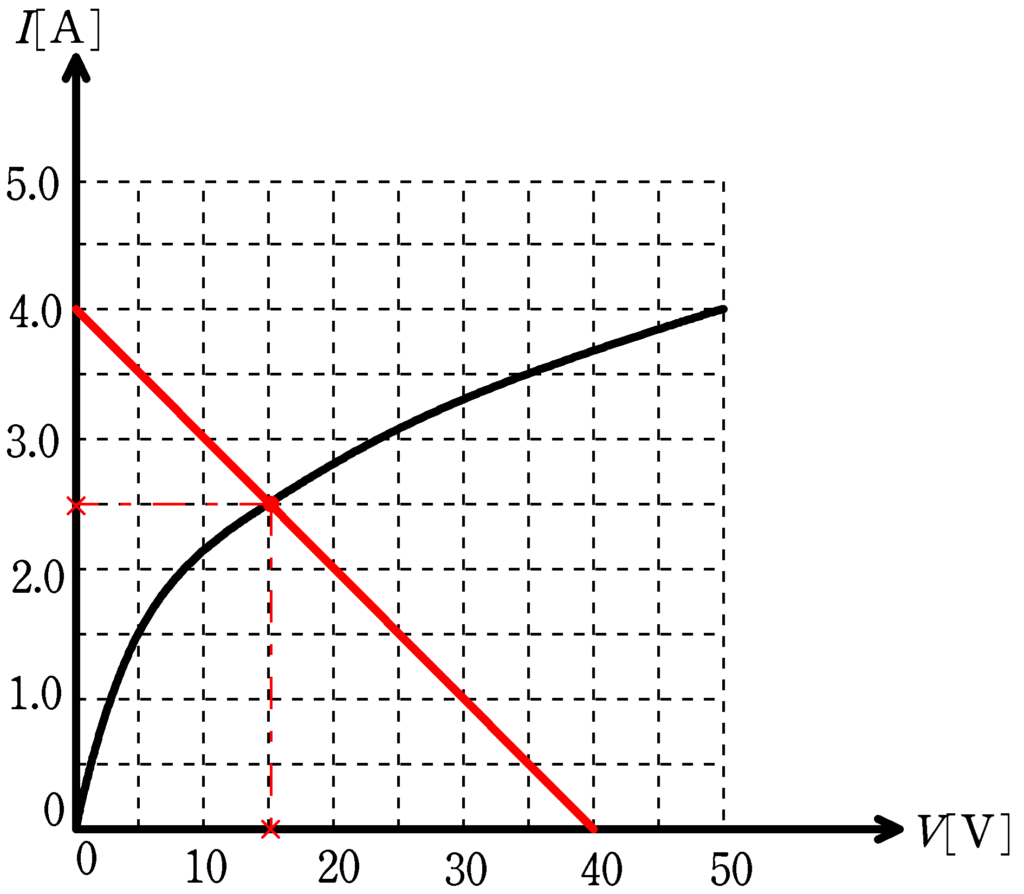
電流は$2.5 \rm A$,電圧は$15 \rm V$(答)
そもそも,特性曲線が与えられたときだけが特別なわけではない

そうそう,こんな感じでやるんだよね.
意味はわからないけど,とりあえず交点を求めているよ.

そもそも,特性曲線が与えられるときだけ特別だと思うから変に思ってしまうのではないでしょうか?
電球が抵抗になってもコンデンサーでもコイルでも普段から同じようなことをやっています.
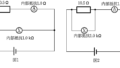
たとえば,次の回路を考えてみましょう.
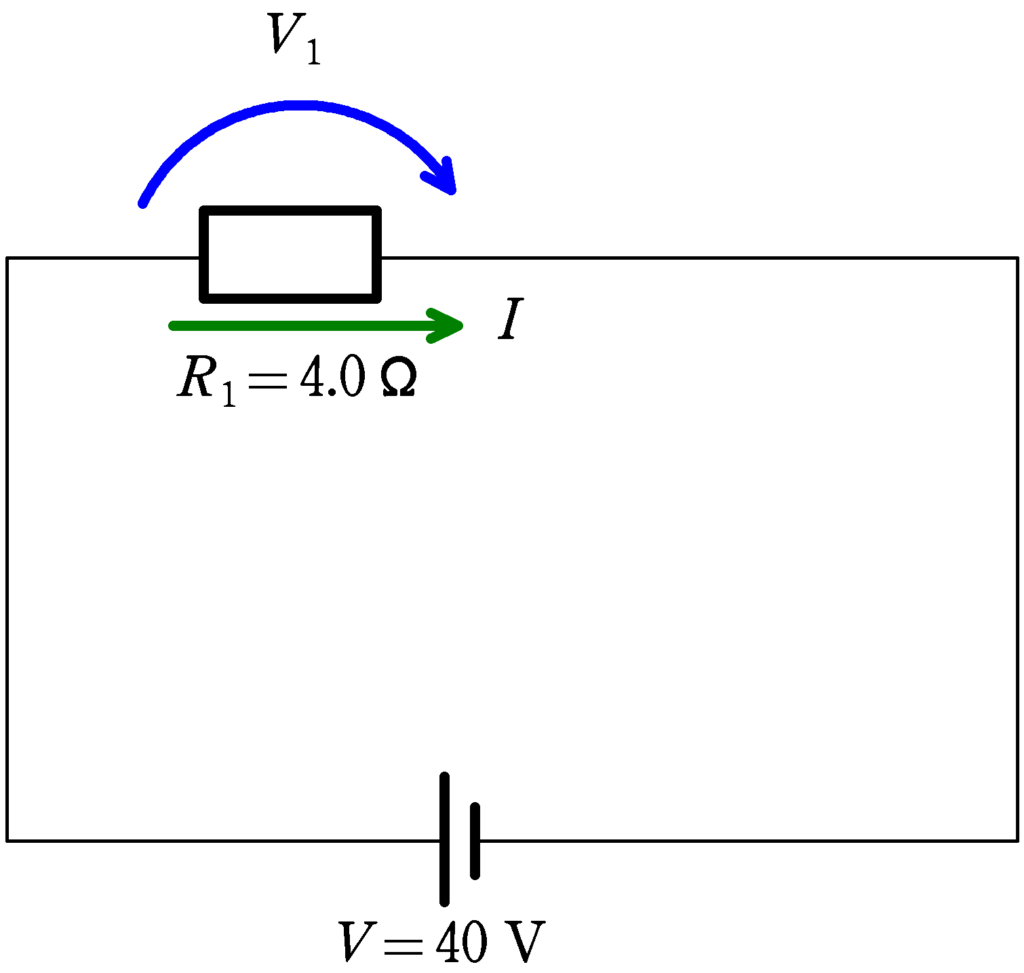

上図において,抵抗に流れる電流を$I$,かかる電圧を$V_{1}$として,キルヒホッフ第2法則とオームの法則をそれぞれ立ててみましょう.
★ キルヒホッフの法則
$40-V_{1}=0$ $\cdots (\ast)$
★ オームの法則
$V_{1}=4.0\times I$ $\cdots (2\ast)$
$(\ast)$,$(2\ast)$より,$V_{1}$を消去して
$40-4.0\times I=0$
$\therefore I=10 \rm A$

普段,面倒だから,オームの法則とキルヒホッフの法則(電圧降下の式)を混ぜて計算していたけど,あえて別々に計算したんだね.
このとき,キルヒホッフの法則で出てきた式とオームの法則から出てきた式を同時に満たす電流$I$を求めたわけか・・・

その通りです.実は,普段からキルヒホッフの法則から出た式とオームの法則やコンデンサーの式,コイルの自己誘導起電力などを連立させて求めていました.
オームの法則は普段,式として出てくるのですが,特性曲線の問題は式ではなくグラフが与えられるわけです.
もう1題解いてみましょう.
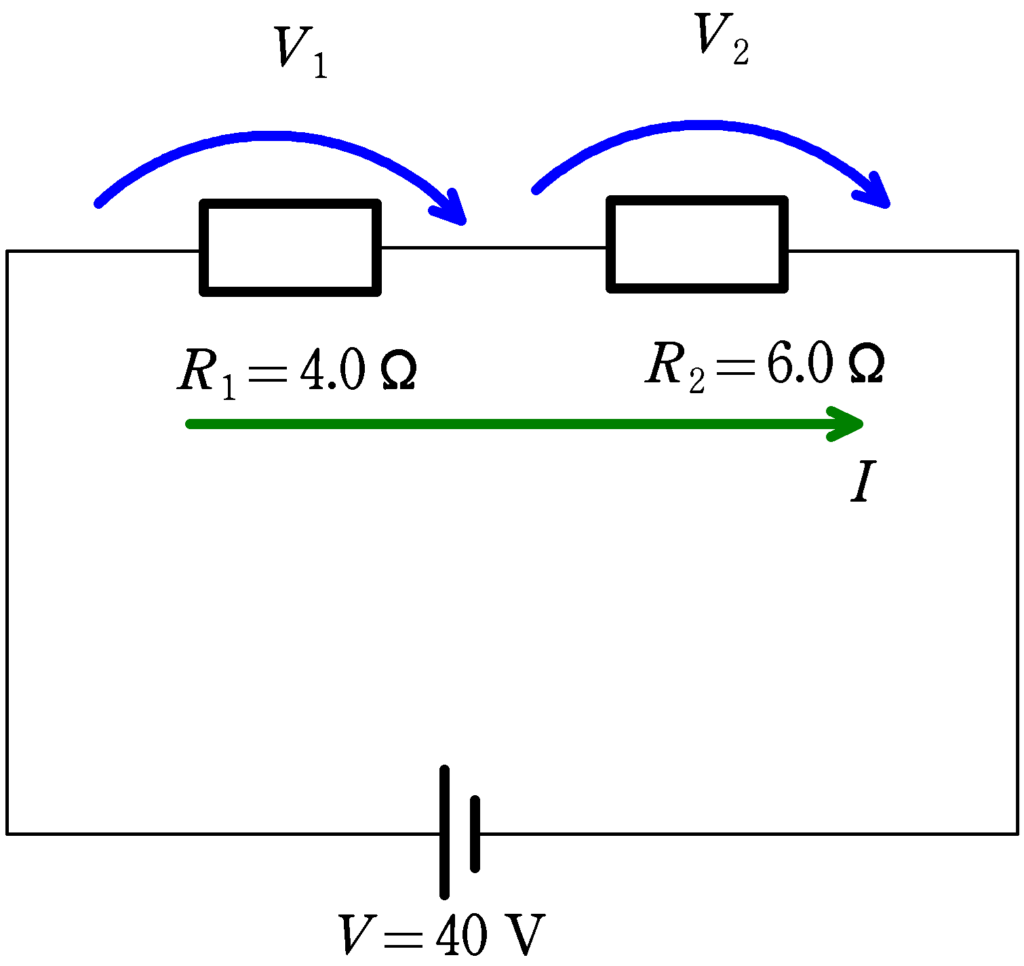

回路に流れる電流を$I[\rm A]$,$R_{1}$と$R_{2}$にかかる電圧をそれぞれ$V_{1} , V_{2}$として,キルヒホッフの法則とオームの法則を立てると,,,
★ キルヒホッフの法則
$40-V_{1}-V_{2}=0$ $\cdots (3\ast)$
★ オームの法則
$V_{1}=4.0\times I$ $\cdots (4\ast)$
$V_{2}=6.0\times I$ $\cdots (5\ast) $
$(4\ast)$,$(5\ast)$を$(3\ast)$に代入して
$40-4.0\times I-6.0\times I=0$
$\therefore I=4.0 \rm A$

これも回路の式とオームの法則を連立させて解いているね.
ということは,回路の式を満たし,かつオームの法則の式を満たす解を探しているわけだ.
特性曲線の問題の場合は,回路の式を満たし,かつ$I$と$V$の関係のグラフを同時に満たす解を探しているから,交点を求めることで解が出るんだね.

コメント