
今回はレンズと球面鏡のまとめです.
レンズ
凸レンズの代表光線
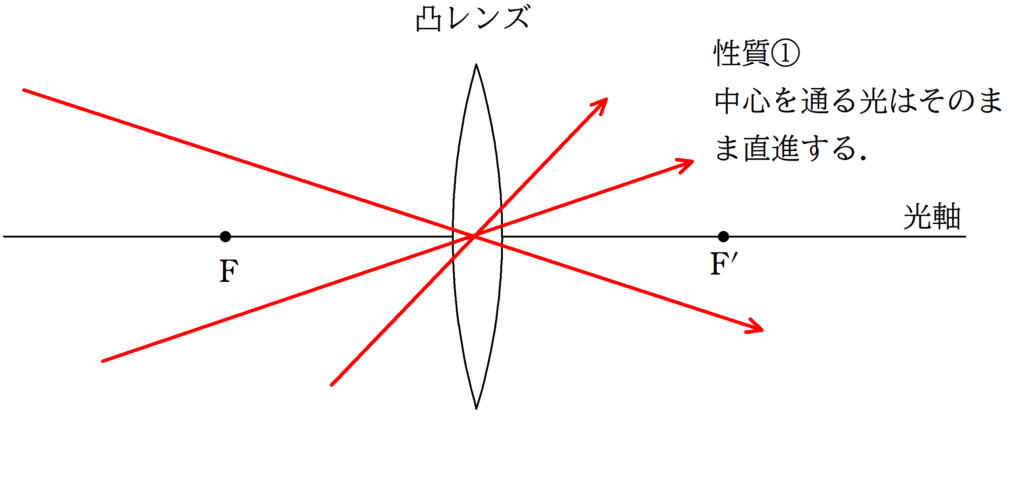
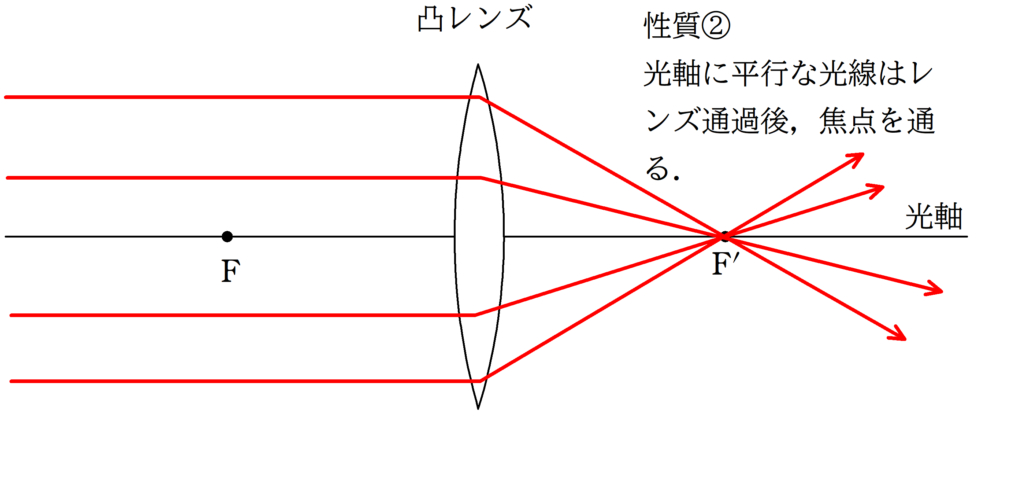
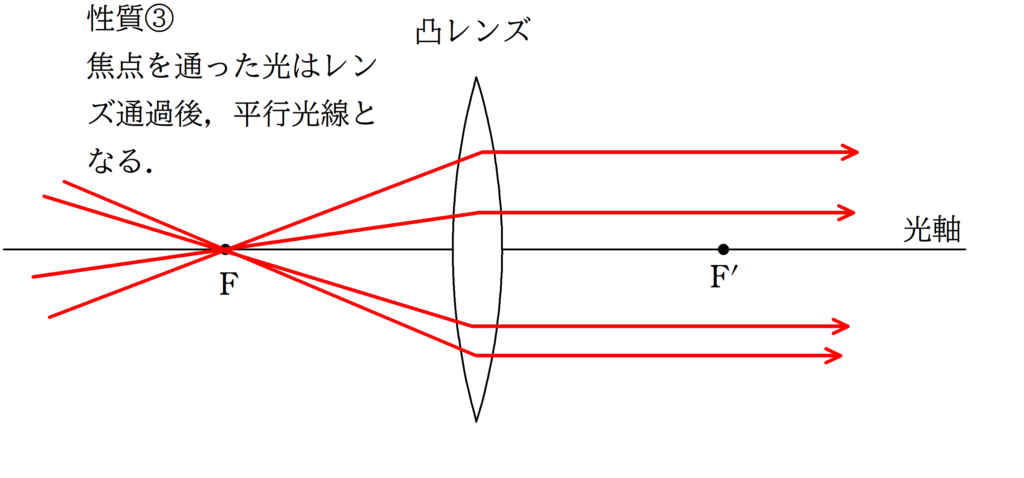

上の3つの代表光線は必ず覚えておきましょう!
凹レンズの代表光線
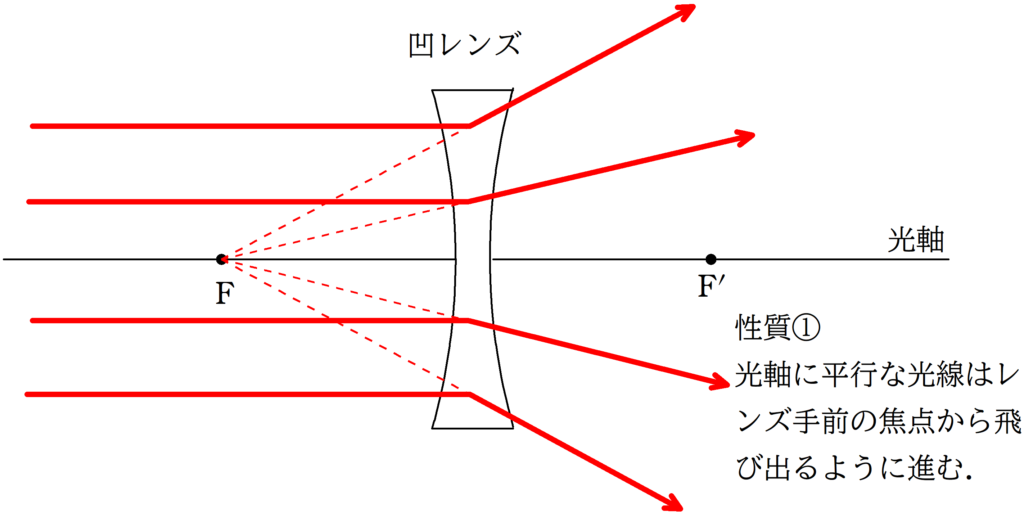
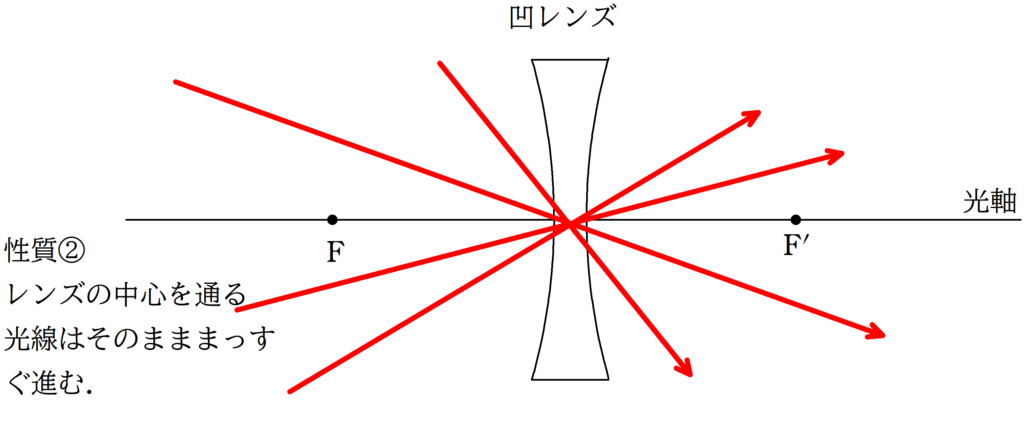
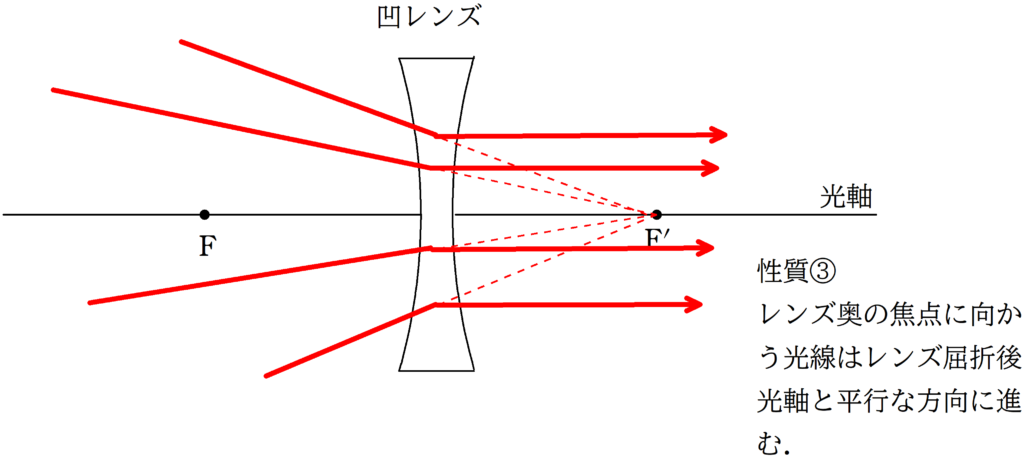

性質①と性質③は光線逆進の原理を知っていれば,区別して覚える必要もありません.
レンズの式
レンズと光源との距離を$|a|$,焦点距離を$|f|$,レンズと像との距離を$|b|$とする.
このとき,次の式が成り立つ.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$
ただし,次の規則で$a$と$b$と$f$の正負を決める.
$a>0 \dots$ 実物体(実光源), $a<0 \dots$ 虚物体(虚光源)
$b>0 \dots$ 実像, $b<0 \dots$ 虚像
$f>0 \dots$ , 凸レンズ $f<0 \dots$ 凹レンズ

上の式は導出もできるようにしておくとよいですね.
組み合わせレンズの作図法
下図の2つのレンズ1,2を考える.
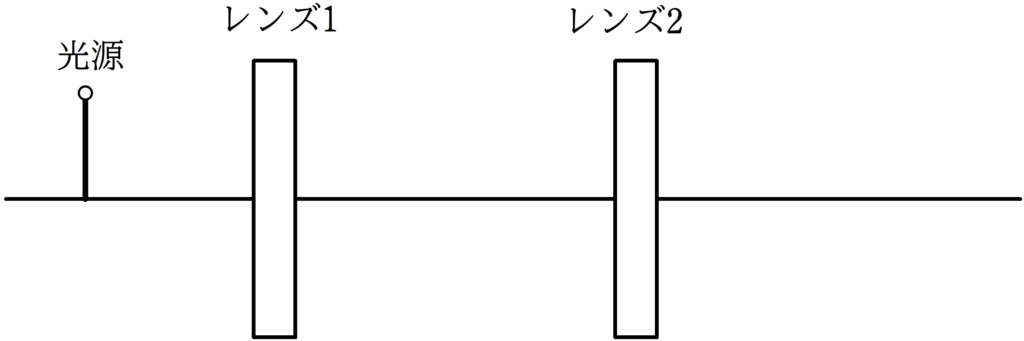
レンズ1の左側に光源を置く.
このとき,次の3つの場合がある.
[1] レンズ1を屈折後,レンズ1とレンズ2の間に実像をつくるとき
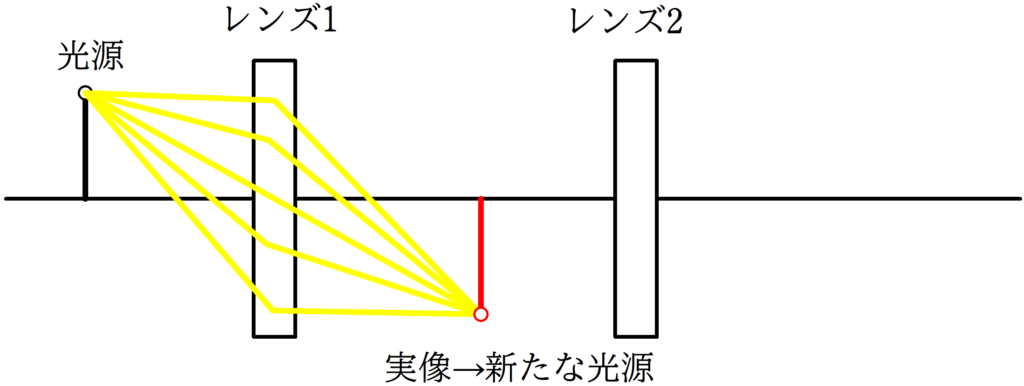
レンズ1とレンズ2の間にできた実像を新たな光源として,レンズ2への屈折を考える.
[2] レンズ1屈折後,レンズ1の左側に虚像ができるとき
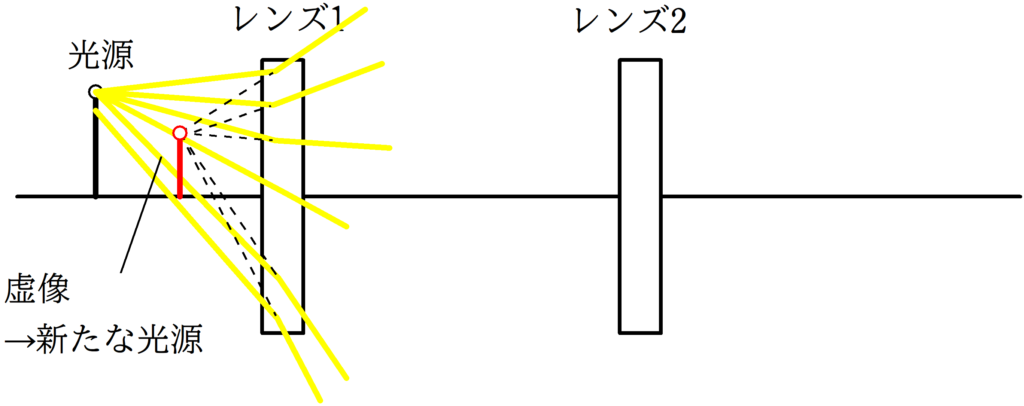
レンズ1の左側にできる虚像を新たな光源としてレンズ2への屈折を考える.
[3] レンズ1屈折後,レンズ2の右側に虚物体(虚光源ができるとき)
(つまり,レンズ2がなかったら,そこに実像ができるとき)
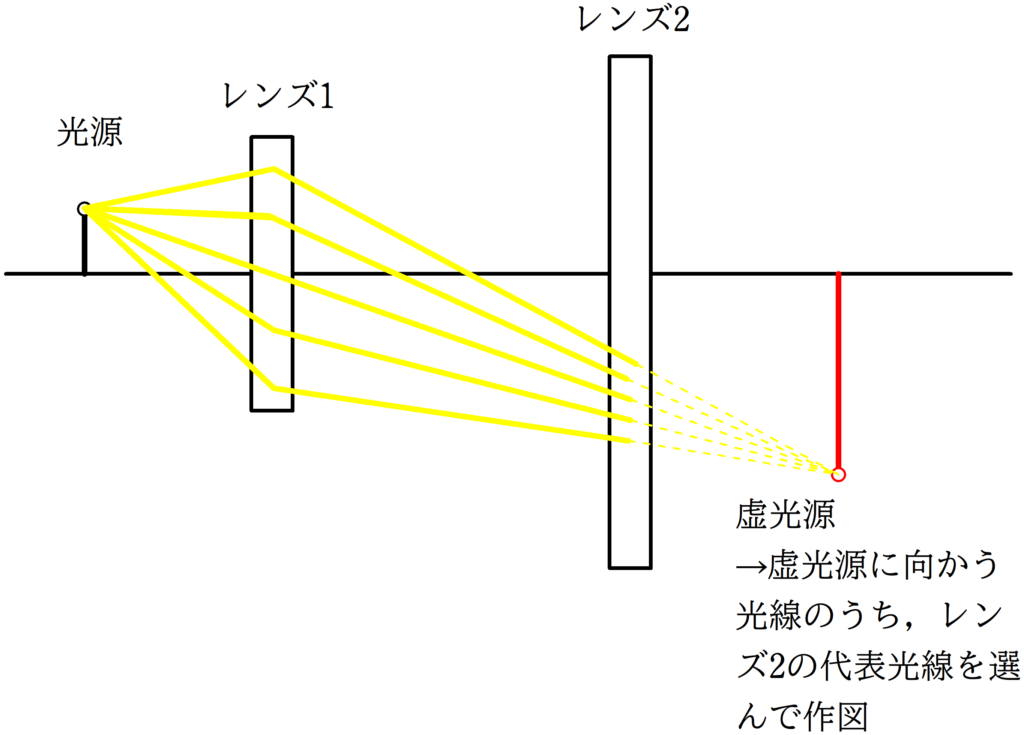
このとき,虚光源を新たな光源とするのではなく,虚光源に向かう光線のうち,レンズ2の代表光線を選んで作図する必要がある.

虚光源の場合の作図は注意が必要だね!
球面鏡
反射の法則

球面鏡の基本は反射です.
次の反射の法則を知っていれば大体の作図ができます.
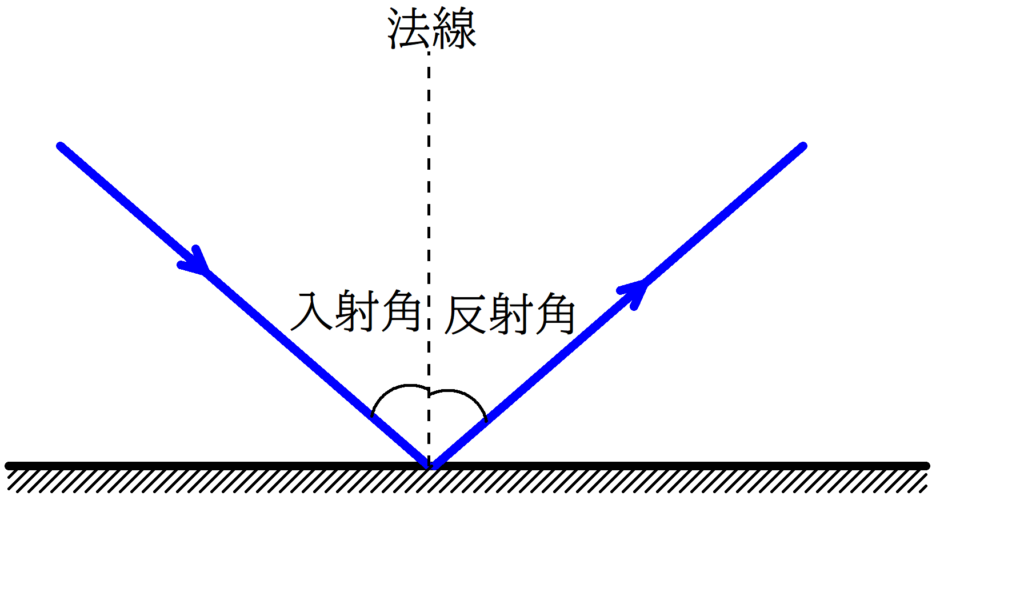
反射面の法線(垂直な線)から入射光線までのなす角を入射角,反射光線までのなす角を反射角という.
このとき
入射角=反射角
が成り立つ.
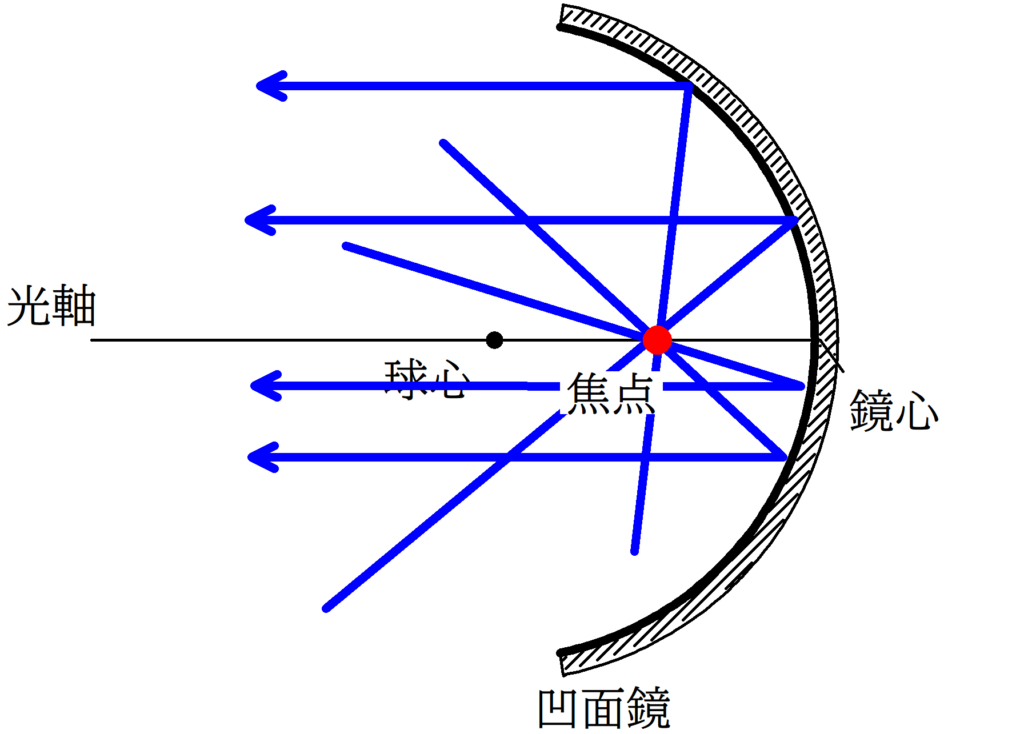
凹面鏡の代表光線
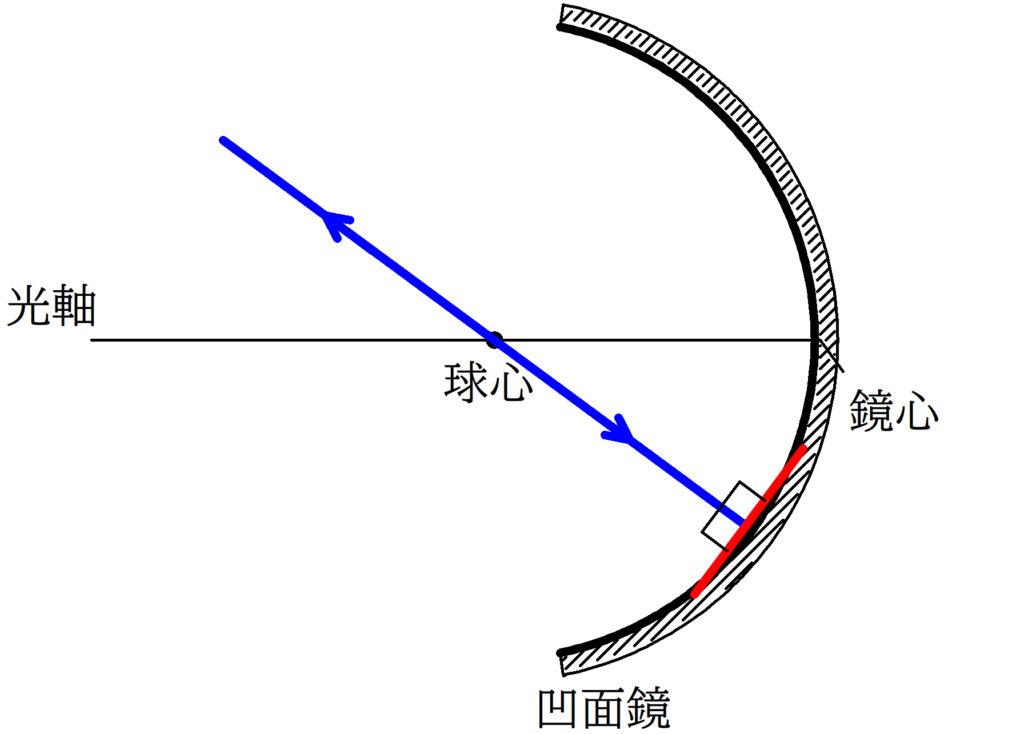
1. 鏡心にあたる光は,反射の法則にしたがって,反射する.
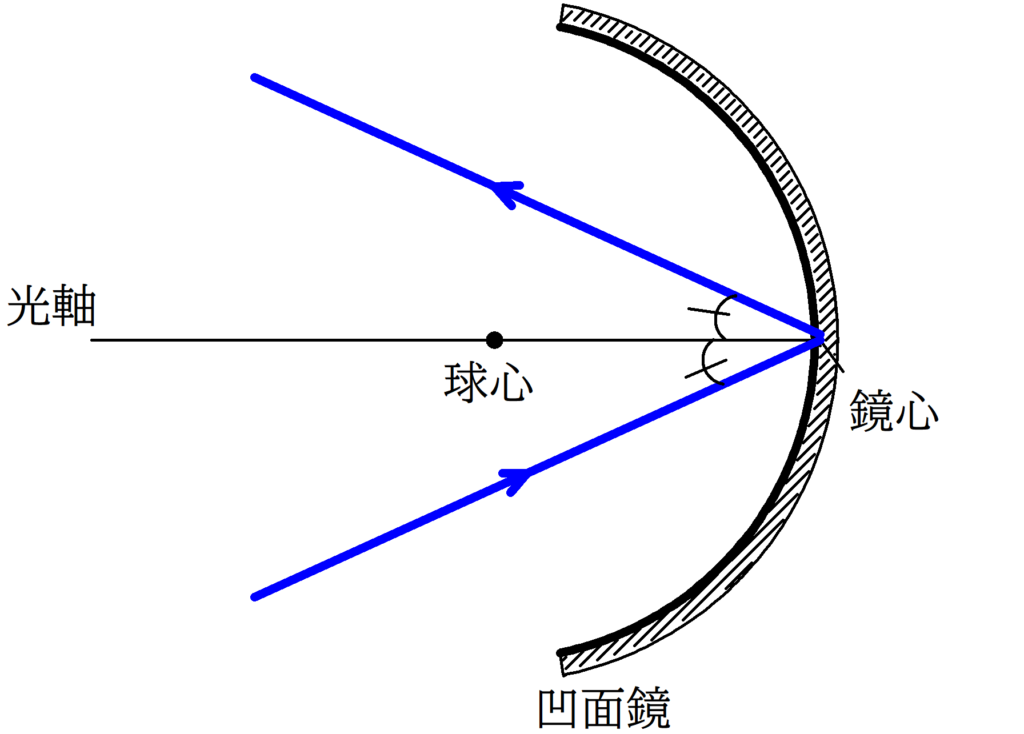
2. 球心を通る光線の入射角は90°なので,反射角も90°である.すなわち,反射光線は入射経路と同じ経路をたどる.
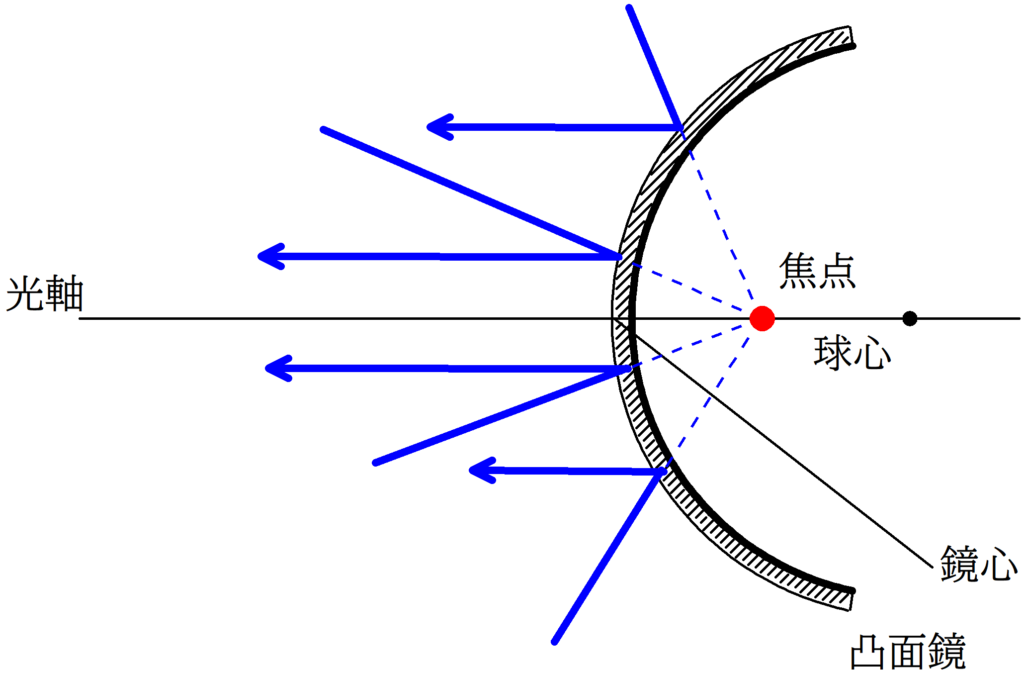
凸面鏡の代表光線
1. 鏡心にあたる光は反射の法則にしたがって,反射する.
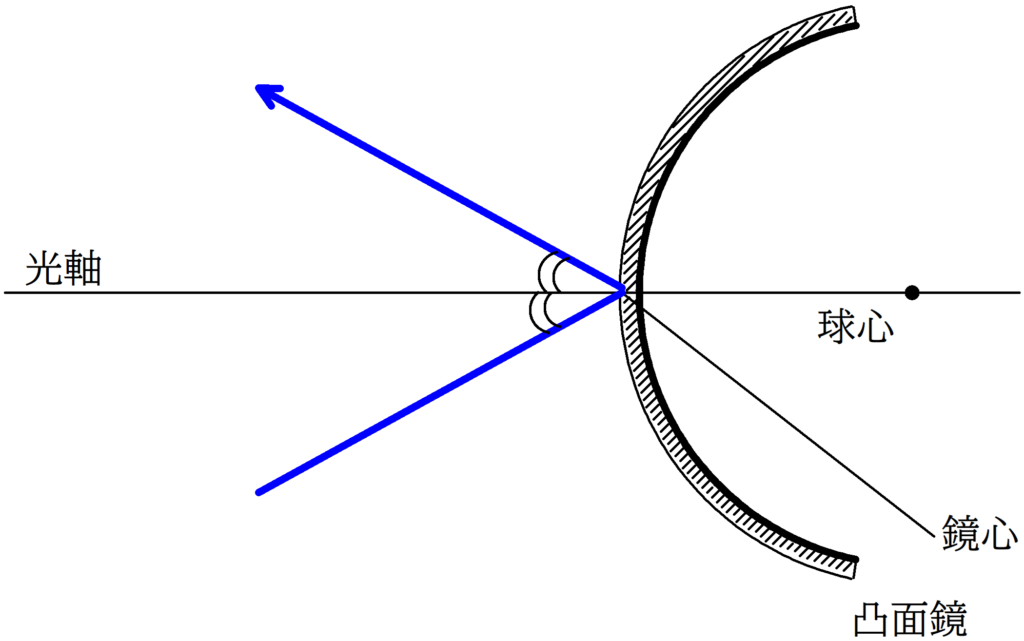
2. 球心を通る光線の入射角は90°なので,反射角も90°である.すなわち,反射光線は入射経路と同じ経路をたどる.
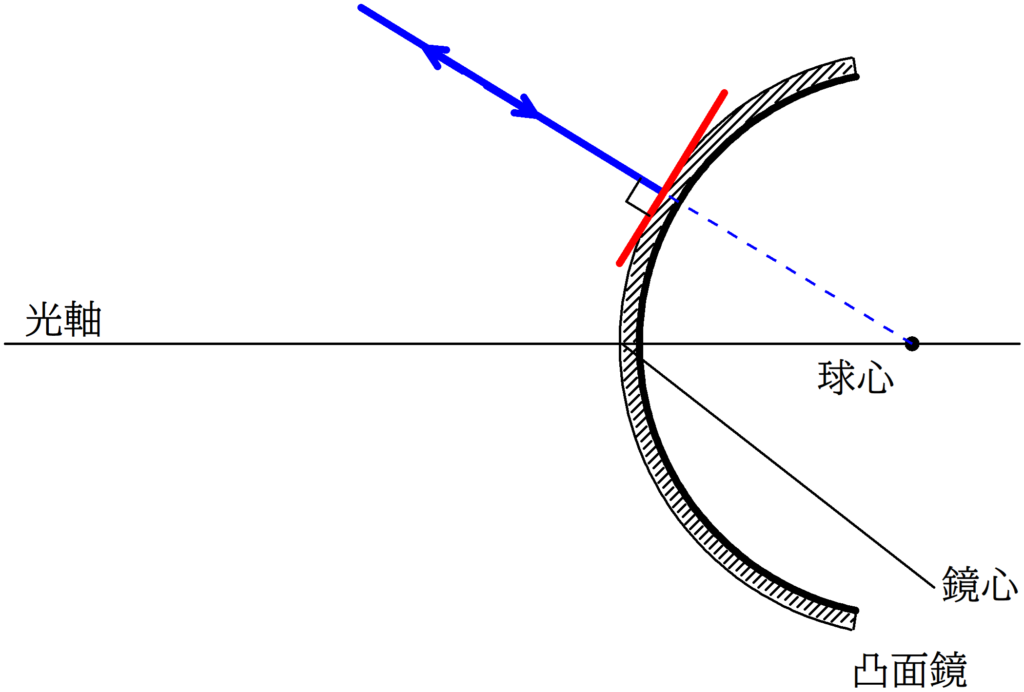
球面鏡の式
球面鏡の鏡心と光源との距離を$|a|$,焦点距離を$|f|$,球面鏡の曲率半径を$|R|$,像との距離を$|b|$とする.
このとき,次の式が成り立つ.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}=\dfrac{2}{R}$
ただし,次の規則で$a$と$b$と$f$の正負を決める.
$a>0 \dots$ 実物体(実光源), $a<0 \dots$ 虚物体(虚光源)
$b>0 \dots$ 実像, $b<0 \dots$ 虚像
$f>0 \dots$ 凹面鏡, $f<0 \dots$ 凸面鏡
球面鏡の焦点と代表光線

球面鏡の焦点は球心と鏡心の中点にあるよ!
1. 光軸に平行な入射光線は凹面鏡反射後焦点を通るように進む.
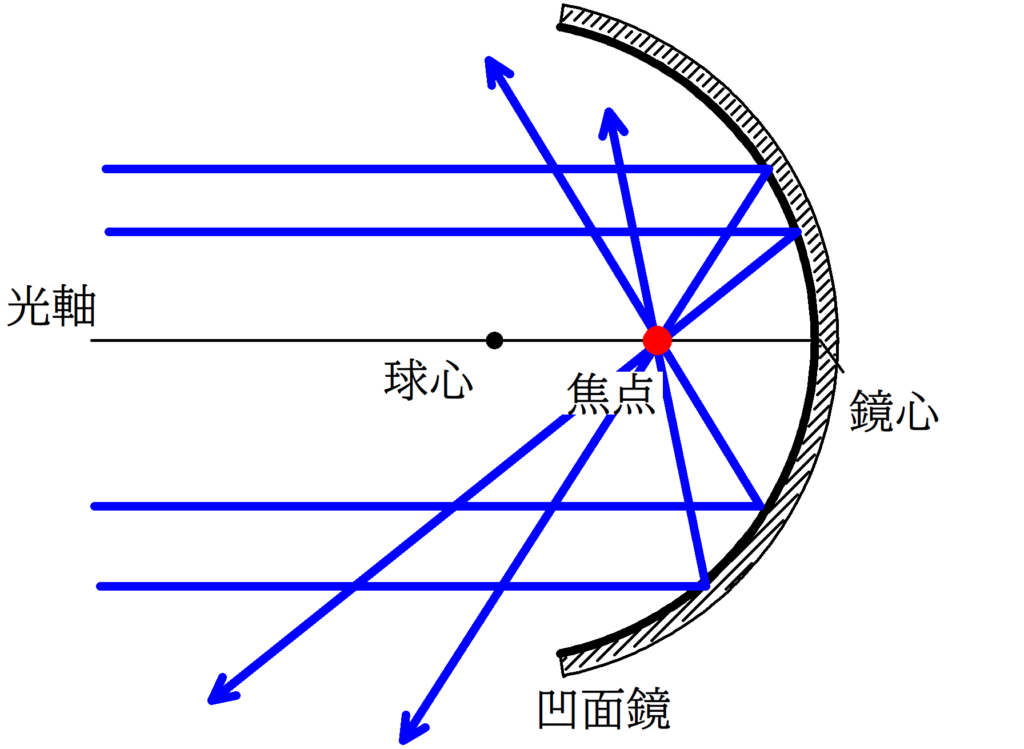
2. 焦点を通る入射光線は凹面鏡反射後,光軸と平行に進む.
1. 光軸に平行な入射光線は,凸面鏡反射後,焦点から飛び出るように進む.
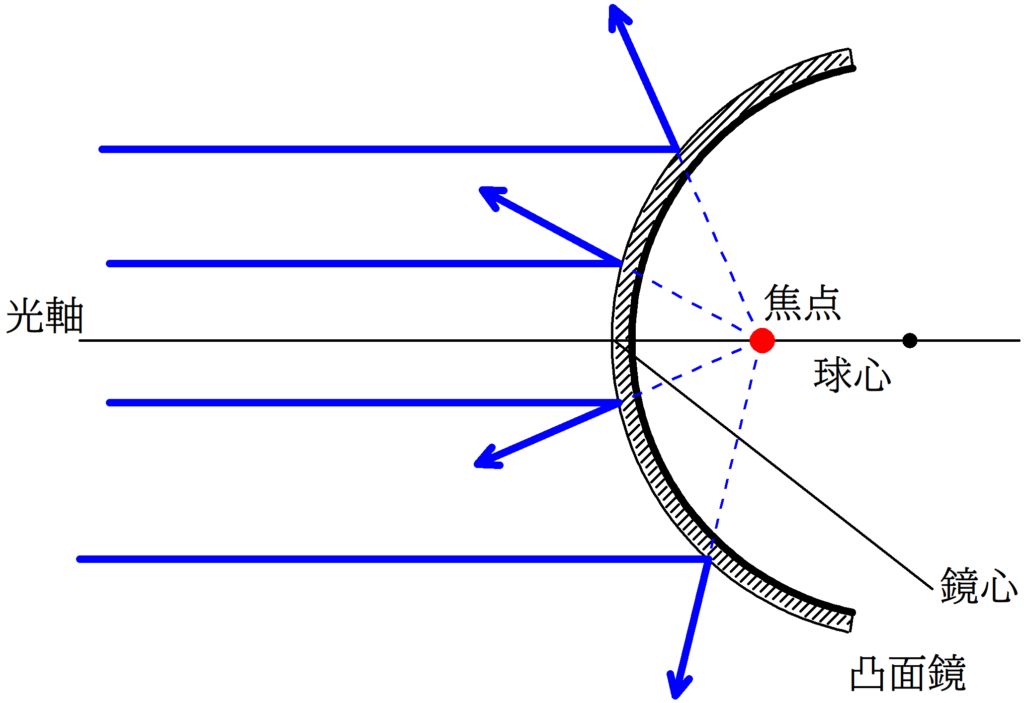
2. 焦点を通る入射光線は,凸面鏡反射後,光軸と平行に進む.


コメント
[…] レンズと球面鏡のまとめ[代表光線と公式] […]