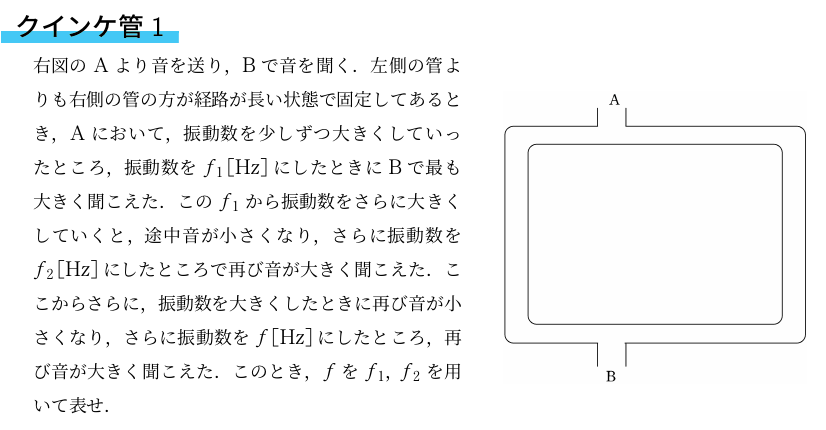
<解答> 位相差についてはこちらを参照してください.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$
左側経路と右側経路の距離の差を$\varDelta x$として,波の波長を$\lambda$とすると,自然数$m$を用いて,強め合いの条件は
$\dfrac{2\pi}{\lambda}\times \varDelta x=2\pi m$ $\cdots (\ast)$
と書けます.ただし,今回は波長ではなく,振動数が与えられているので,振動数を$F$,音の速さを$V$とすると,波の基本式より
$V=F\lambda$ $\therefore\,\, \dfrac{1}{\lambda}=\dfrac{F}{V}$ $\cdots (2\ast)$
$(2\ast)$を$(\ast)$に代入して
$\textcolor{blue}{\dfrac{2\pi F}{V}\times \varDelta x=2\pi m}$ $\cdots (3\ast)$
となります.
振動数$f_{1}$のときの位相差を$2\pi m$とすると,$(3\ast)$より
$\dfrac{2\pi f_{1}}{V}\times \varDelta x=2\pi m$ $\cdots (4\ast)$
$f_{1}<f_{2}$なので,振動数を$f_{2}$にすると,位相差は大きくなります.このとき,音が大きく聞こえたので,位相差は$2\pi m$から$2\pi m+2\pi$となります.
$\dfrac{2\pi f_{2}}{V}\times \varDelta x=2\pi m+2\pi$ $\cdots (5\ast)$
$(4\ast)$と$(5\ast)$から$2\pi m$を消去し,$\varDelta x$を求めてしまいます.
\begin{align*} &\dfrac{2\pi f_{2}\varDelta x}{V}=\dfrac{2\pi f_{1}\varDelta x}{V}+2\pi\\ &\therefore\,\, \dfrac{2\pi(f_{2}-f_{1})\varDelta x}{V}=2\pi\\ &\therefore\,\, \varDelta x=\dfrac{V}{f_{2}-f_{1}} \cdots (6\ast) \end{align*}
さらに$(6\ast)$を$(4\ast)$に代入すると,$2\pi m$が計算できます.
\begin{align*} 2\pi m &=\dfrac{2\pi f_{1}}{V}\times \dfrac{V}{f_{2}-f_{1}}\\ &=\dfrac{2\pi f_{1}}{f_{2}-f_{1}} \cdots (7\ast) \end{align*}
さらに,振動数$f$のときの強め合いの条件を立てます.このときの位相差はさらに$2\pi$増えた$2\pi m+4\pi$です.
$\dfrac{2\pi f}{V}\times \varDelta x=2\pi m+4\pi$
この式に$(5\ast)$と$(6\ast)$を代入して$f$を求めていきます.
\begin{align*} &\dfrac{2\pi f}{\cancel{V}}\times \dfrac{\cancel{V}}{f_{2}-f_{1}}=\dfrac{2\pi f_{1}}{f_{2}-f_{1}}+4\pi\\ &\therefore f=\textcolor{red}{2f_{2}-f_{1}\,\,[\rm Hz] (答)} \end{align*}



コメント