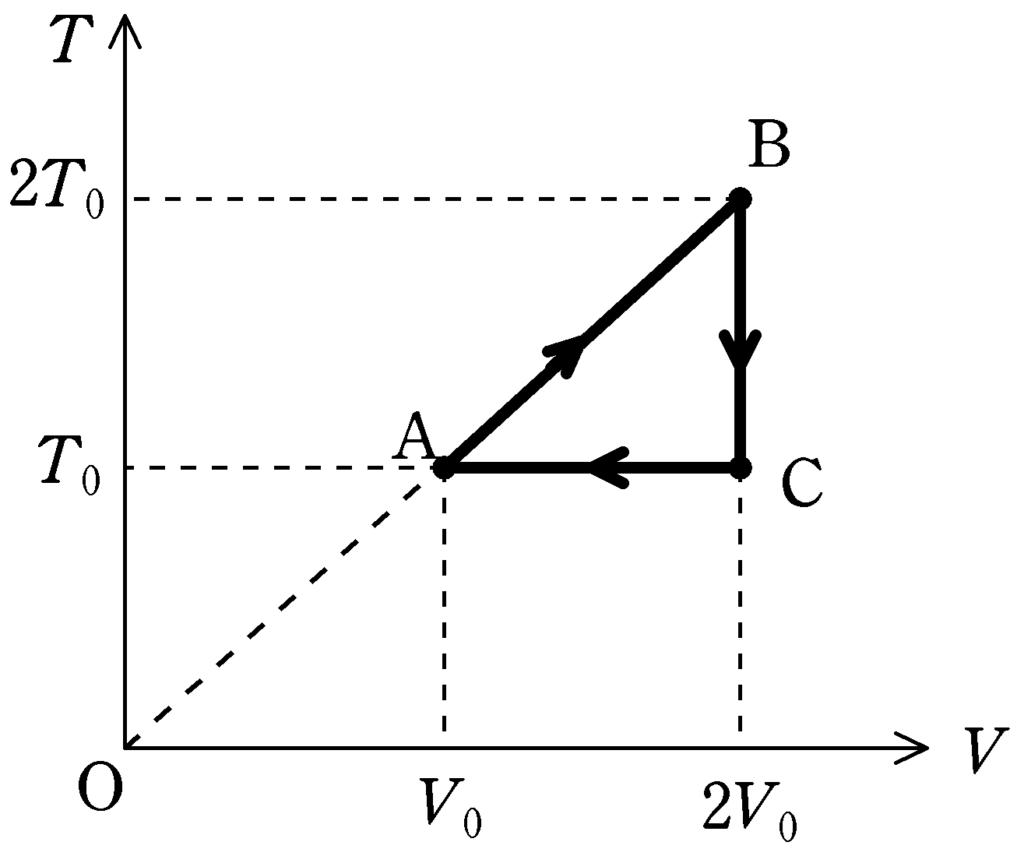
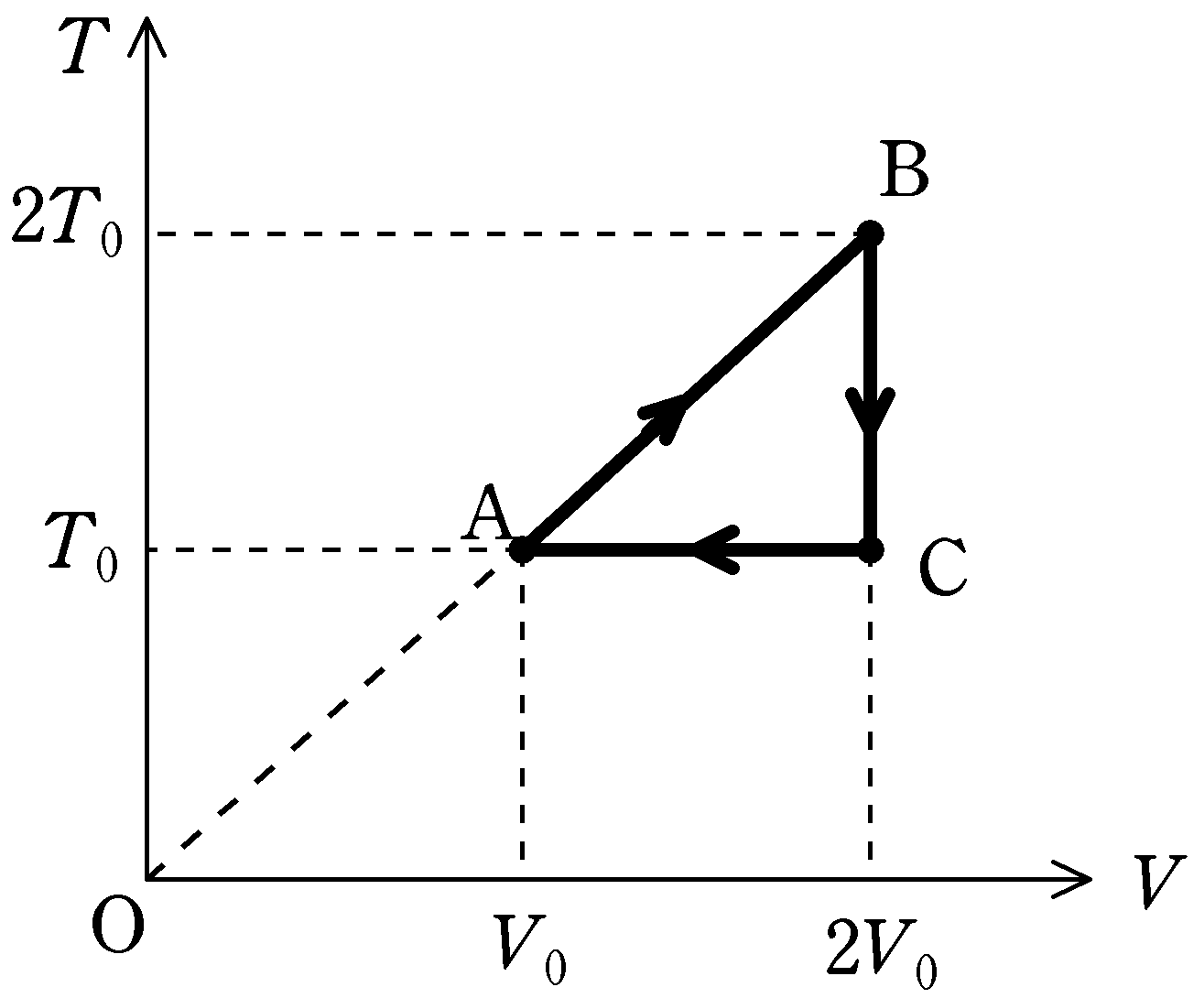
理想気体を状態A$\to$B$\to $C$\to $Aと変化させた.そのときの絶対温度$T$と体積$V$の関係は上図のように表される.ただし,直線ABは原点Oを通る直線である.状態Aでの圧力を$P_{0}$とする.このとき,縦軸を圧力$P$,横軸を体積$V$とした$PV$図をかけ.
<解答>
① A$\to $Bについて
$TV$図をみると,A$\to $Bでは$T$と$V$は比例関係にある.つまり,比例定数$\alpha$を用いれば
$T=\alpha V$ $\cdots (\ast)$
の関係があります.一方,ボイル・シャルルの法則より,
理想気体について,物質量$n$が変化しないとき,気体の圧力を$p$,気体の体積を$V$,絶対温度を$T$とすると,
$\dfrac{pV}{T}=$一定
が成り立つ.(ボイル・シャルルの法則)
特に,温度が一定のとき
$pV=$一定(ボイルの法則)
圧力が一定のとき
$\dfrac{V}{T}=$一定(シャルルの法則)
が成り立つ.
$\dfrac{V}{T}=$一定$(=\alpha)$なら,$(\ast)$と同じ式になります.
したがって,A$\to $Bは定圧変化です.
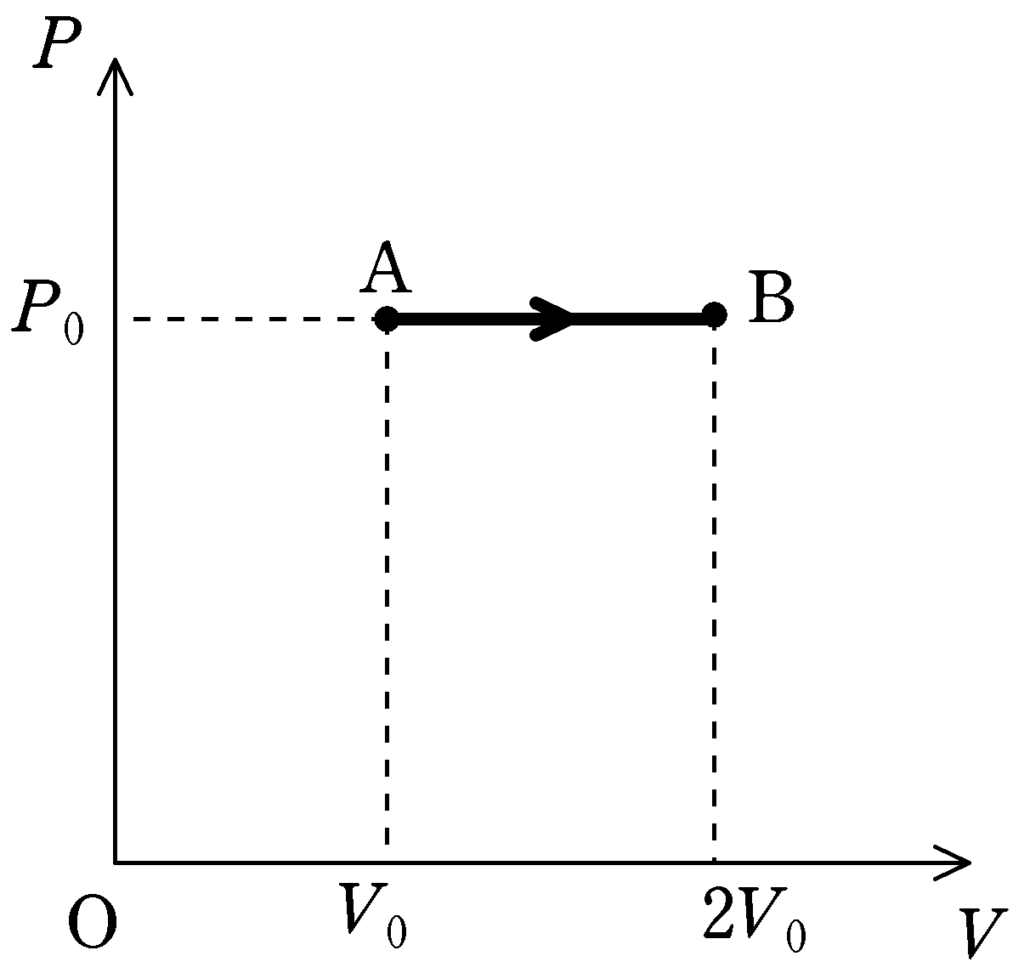
② B$\to $Cについて
B$\to$Cは体積一定のまま温度が下がっているので,定積変化です.
状態Cでの圧力を$P_{\rm C}$として,状態Aと状態Cでボイル・シャルルの法則を立てて,$P_{\rm C}$を求めます.
\begin{align} &\overbrace{\dfrac{P_{0}V_{0}}{T_{0}}}^{状態 \rm A}=\overbrace{\dfrac{P_{\rm C}\times 2V_{0}}{T_{0}}}^{状態 \rm C}\\ &\therefore\,\,\, P_{\rm C}=\textcolor{red}{\dfrac{1}{2}P_{0}} \end{align}
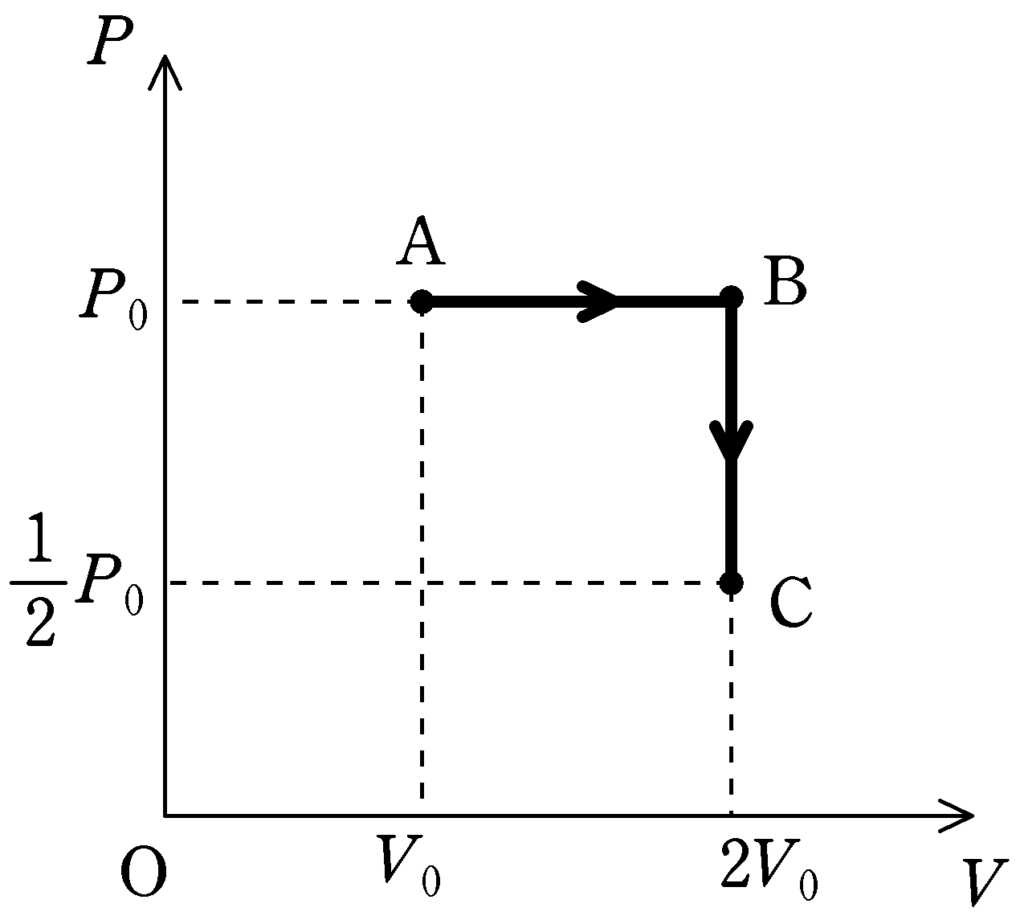
③ C$\to $Aについて
C$\to$Aは温度を一定のまま体積を小さくしているので,等温変化.
$T=$一定のときは状態方程式より
$PV=nRT=$一定
$\therefore\,\, \textcolor{blue}{P}=\dfrac{一定}{\textcolor{green}{V}}$
が成り立つので,
\begin{align*} \textcolor{blue}{y}=a\textcolor{green}{x} \end{align*}
と同じ形の反比例のグラフのようになります.
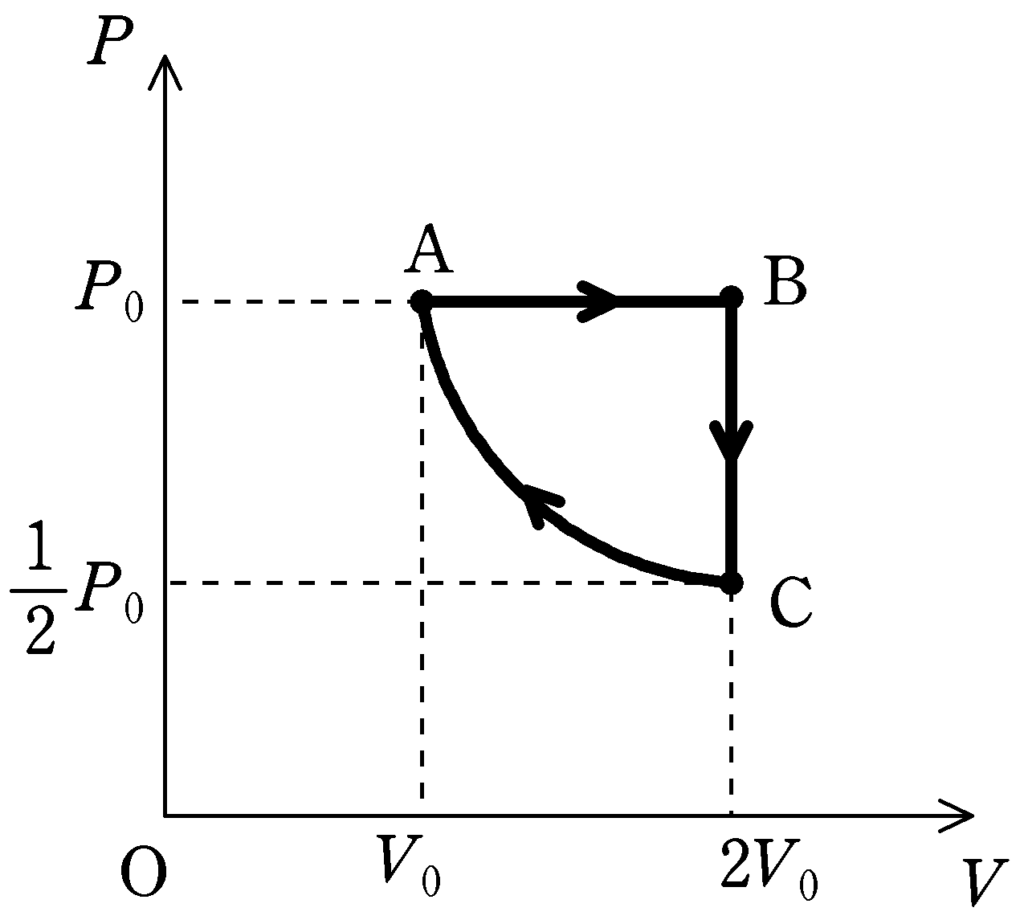
ということで,$PV$図になおすと,上図のようになります.(終)


コメント