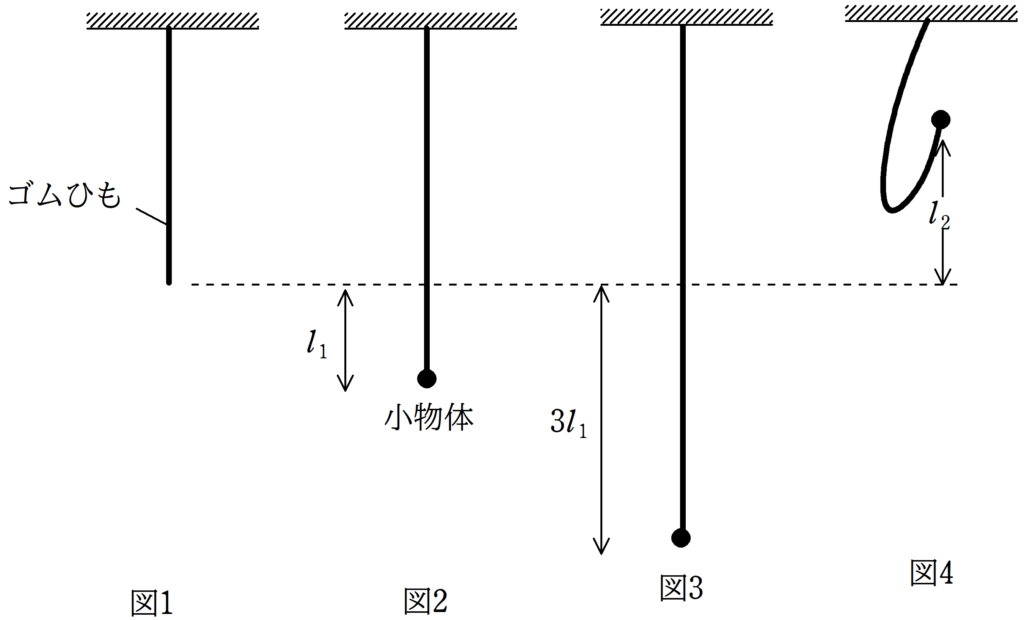
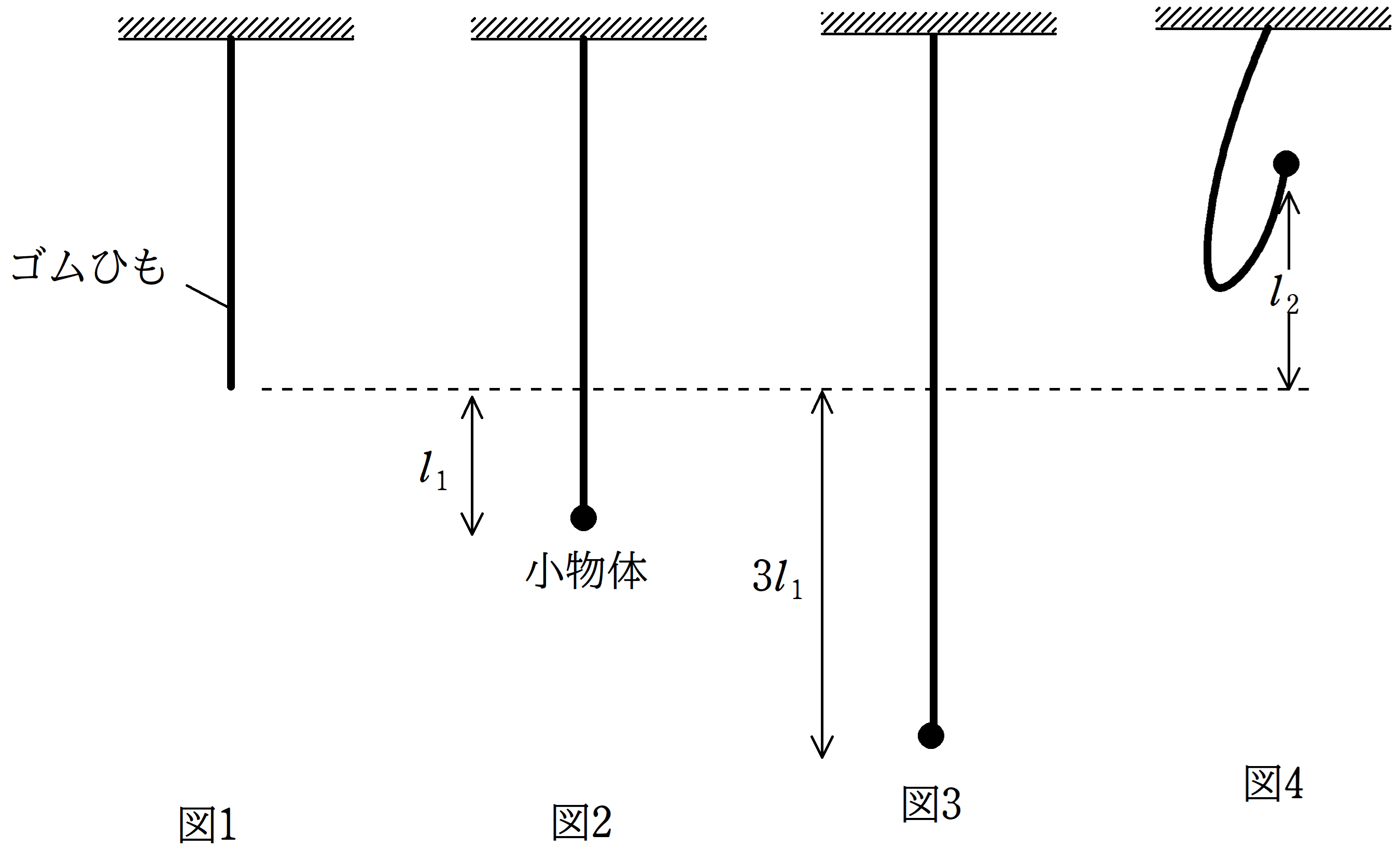
図1のように質量の無視でき,伸びているときはばね定数が$k$のばねと同等とみなし,たるんでいるときは,物体になんの力も及ばさないゴムひもが天井につるされている.
図1の状態から,質量$m$で大きさの無視できる小物体をゴムひもに取りつけたところ,ゴムひもは自然長より$l_{1}$だけ伸びて静止した.(図2)
図2の状態からさらに$2l_{1}$だけゴムひもを伸ばし静かに離したあと,小物体は単振動をはじめた.しかし,ばねが自然長にもどるとゴムひもはたるみ,小物体には重力のみがはたらき等加速度運動をした.
重力加速度の大きさを$g$として,次の問いに答えよ.
(1) $l_{1}$を$m, g, k$を用いて表せ.
(2) 図3の状態から小物体を静かに離した後,しばらくはある周期とある振幅の単振動の一部の運動をする.このとき,単振動の周期と振幅を$m, g, k$から必要なものを用いて表せ.
(3) 図3の状態から小物体を静かに離した後,ゴムひもが自然長になったときの小物体の速さ$v_{0}$を$m, g, k$から必要なものを用いて表せ.
(4) (3)の後,小物体が最高点に達したときに,ゴムひもが自然長の状態であった場所からどれだけ離れているか.その距離$l_{2}$を$m, g, k$を用いて表せ.
<解答>
(1)
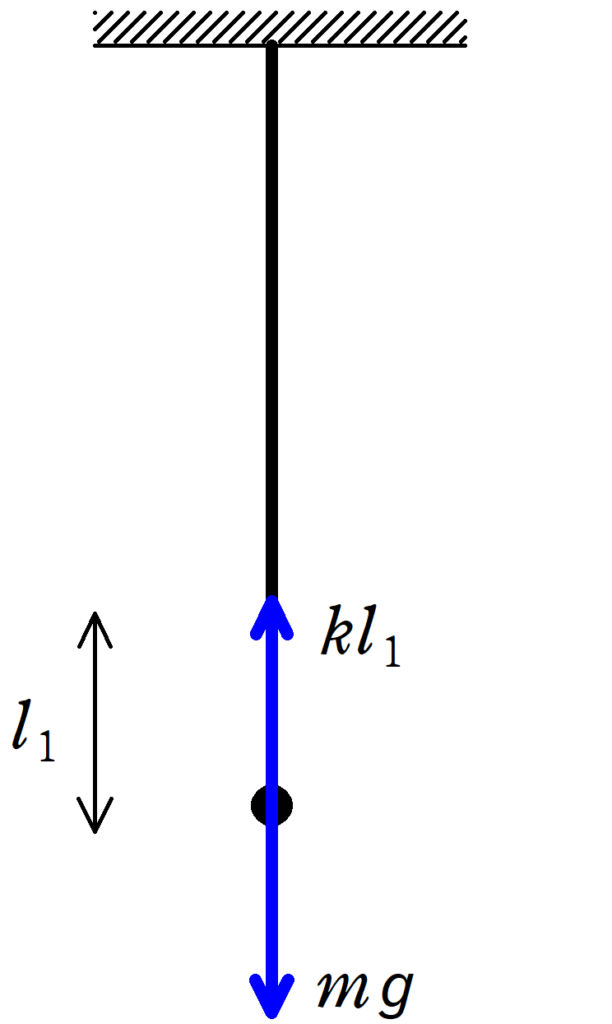

小物体が静止しているので,つり合いの式を立ててみましょう.
小物体にはたらく力は重力$mg$とゴムひもによる力$kl_{1}$です.
★ 小物体のつり合いの式
$kl_{1}=mg$ $\therefore l_{1}=\dfrac{mg}{k}$ (答)
(2)

単振動の情報を読み取るために,運動方程式を立てます.
ゴムひもが自然長である位置を原点とし,鉛直下向きを正として$y$座標をとりましょう.
座標$y$において小物体にはたらく力は鉛直下向きに重力$mg$と鉛直上向きにゴムひもによる力$ky$です.
$y$座標の向きに加速度$a$を設定すると,運動方程式は次のようになります.
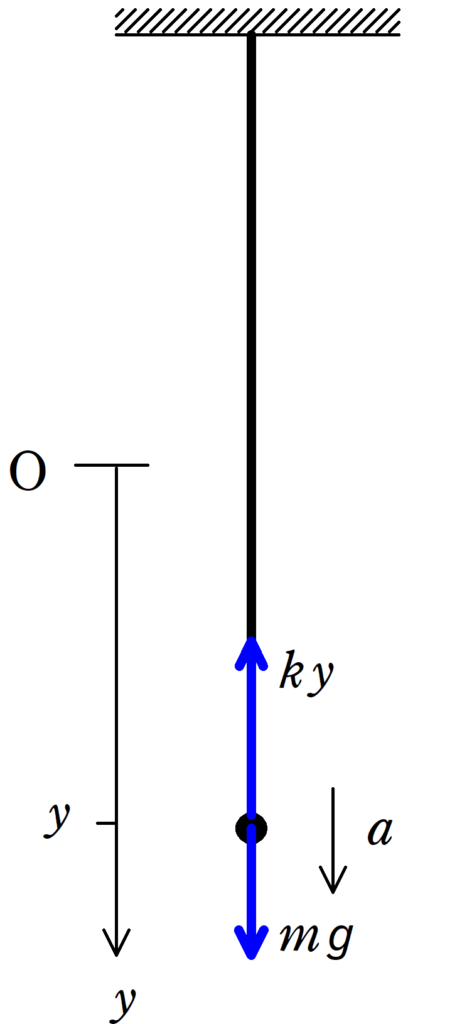
★ 運動方程式
$ma=mg-ky=-k(y-\dfrac{mg}{k})$
質量を$m$,加速度を$a$,物体の座標を$x$,$x_{0}$を定数,$k$を正の定数とする.
運動方程式が以下で表されている.
$ma=-k(x-x_{0})$
このとき,振動の中心は$x_{0}$,角振動数$\omega$と周期$T$は次のようになる.
$\omega=\sqrt{\dfrac{k}{m}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$

この運動方程式から,振動の中心$y_{0}$と周期$T$は
$y_{0}=l_{1}=\dfrac{mg}{k}$
$T=2\pi\sqrt{\dfrac{m}{k}}$ (答)
となるね.
さらに,振幅$A$は中心と単振動の下端までの距離だから
$A=3l_{1}-l_{1}=2l_{1}=\dfrac{2mg}{k}$ (答)
となります.
(3)

運動方程式を立てたので,単振動のエネルギー保存則を使って自然長$y=0$での小物体の速さを求めてみましょう.
単振動の運動方程式が
$ma=-k(x-x_{0})$
になるとき,単振動のエネルギー保存
$\dfrac{1}{2}mv^{2}+\dfrac{1}{2}k(x-x_{0})^{2}=$一定
が成り立つ.
※ $(x-x_{0})^{2}$は中心からの距離の2乗を表している.自然長からの距離ではない.
※ 上記の運動方程式を変形したものなので,摩擦力や重力がはたらいてもその仕事をいれないでよい.
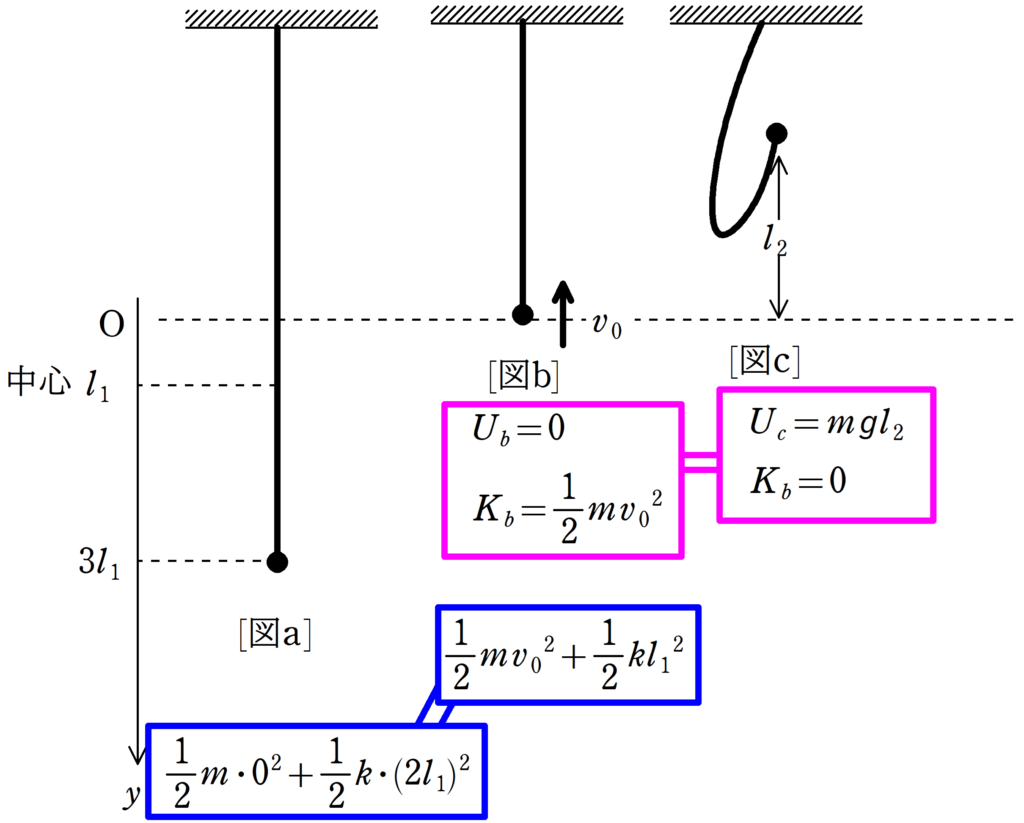

はじめの単振動のエネルギーは,速度が$0$であることと,中心からの距離が$3l_{1}-l_{1}=2l_{1}$なので,
$\dfrac{1}{2}m\cdot 0^{2}+\dfrac{1}{2}k(2l_{1})^{2}$
です.
そして,自然長つまり,$y=0$での単振動のエネルギーは,速さを$v_{0}$,振動の中心からの距離$l_{1}$であることを考慮して
$\dfrac{1}{2}mv_{0}^{2}+\dfrac{1}{2}kl_{1}^{2}$
となります.
★ 単振動のエネルギー保存則
$\eqalign{\dfrac{1}{2}k(2l_{1})^{2}&=\dfrac{1}{2}mv_{0}^{2}+\dfrac{1}{2}kl_{1}^{2}\cr mv_{0}^{2}&=3kl_{1}^{2}\cr v_{0}^{2}&=\dfrac{3kl_{1}^{2}}{m}=\dfrac{3k}{m}(\dfrac{mg}{k})^{2}=\dfrac{3mg^{2}}{k}\cr v_{0}&=g\sqrt{\dfrac{3m}{k}}}$
したがって,答えは$v_{0}=g\sqrt{\dfrac{3m}{k}}$
(4)

最後は力学的エネルギー保存則です.

★ 力学的エネルギー保存則
重力による位置エネルギーの基準点をゴムひもの自然長の位置にとって
$\eqalign{\dfrac{1}{2}mv_{0}^{2}+0&=mgl_{2}+0\cr l_{2}&=\dfrac{v_{0}^{2}}{2g}=\dfrac{1}{2g}\cdot g^{2}\dfrac{3m}{k}=\dfrac{3mg}{2k}}$
したがって,$l_{2}=\dfrac{3mg}{2k}$


コメント
(2)について質問です.
復元力の有無でゴム紐がたるむ前と後では運動が変わると思います.それに伴って運動方程式も変わると思います.そして周期も単振動のものとは異なると思うのですが,どうでしょうか?
ご指摘ありがとうございます.
その通りです.
この問題はそこまで難しくするつもりはなく,単純に単振動をしている際に「単振動がずっと続いているという仮定のもとで」,周期を聞いているつもりでした.
ただ,問題がわかりずらかったので,変えてみます.
ちなみに,minoru tanakaさんの意図する「振動の周期」であれば,
★ 出発から自然長になるまで→$\dfrac{1}{3}T$
★ 自然長から最高点に達するまで→$\sqrt{\dfrac{3m}{k}}$
この2倍分が振動の周期なので,$\dfrac{4\pi}{3}\sqrt{\dfrac{m}{k}}+2\sqrt{\dfrac{3m}{k}}$となります.