
今回は,動摩擦力を含む運動方程式の問題です.
動摩擦力についてまとめておきましょう.
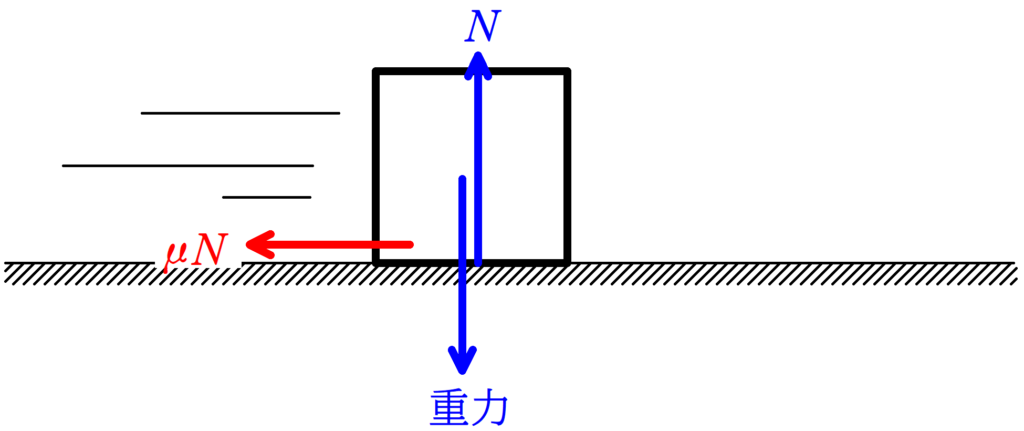
接触面に対して,速度の向きと反対の方向に動摩擦力がはたらく.
接触面の垂直抗力の大きさを$N$,接触面との動摩擦係数を$\mu$とすれば,動摩擦力の大きさ$f$は
$f=\mu N$
である.

動摩擦力の大きさを$\mu mg$と覚えている人がいますが,垂直抗力はいつも$N=mg$とは限りません.
未知な力は
- 運動方程式
- つり合いの式
などで求めます.

次のことを確認したら,問題を解いていきましょう!
質量$m$の物体に力$F$がはたらいているとき,物体の加速度$a$をすると,次の関係式が成り立つ.
$ma=F$
これを運動方程式という.
運動方程式を立てる際には
1. +の向きを決め,その+の向きを加速度の向きとする.
2. 物体の速度の向きとは関係なく,はたらく力をかき,運動方程式を立てる.
3. 力の向きは1.で決めた正の方向であれば,正とし,負の方向に向いていれば負としてかく.
力を図示する流れ
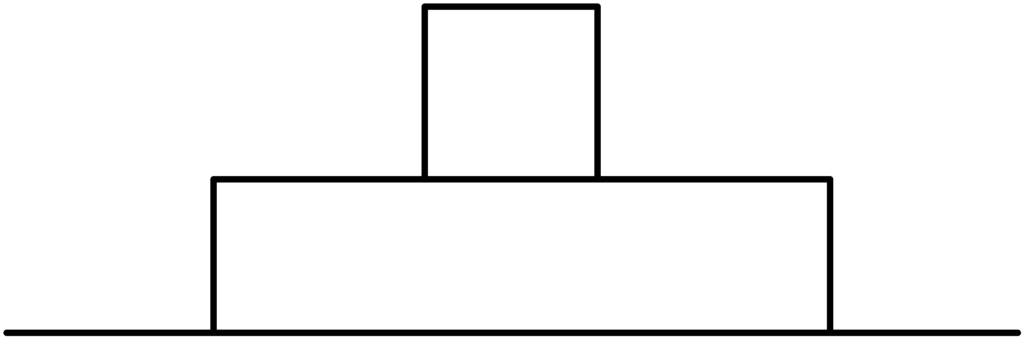
1. 力を図示する物体をきめる.(以後,対象物体とよぶ.)
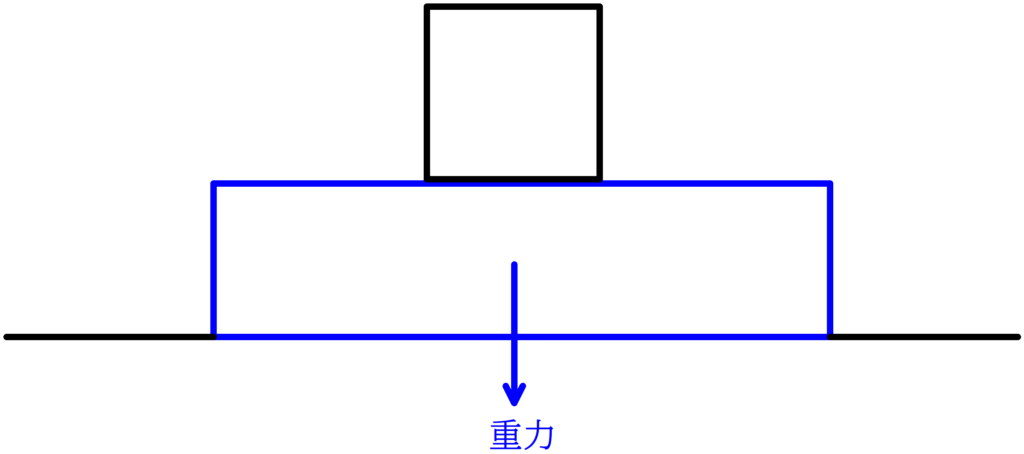
2. まず重力をかく.
3. 対象物体が他の物体と接触している部分に着目し,その場所にはたらく力をかく.
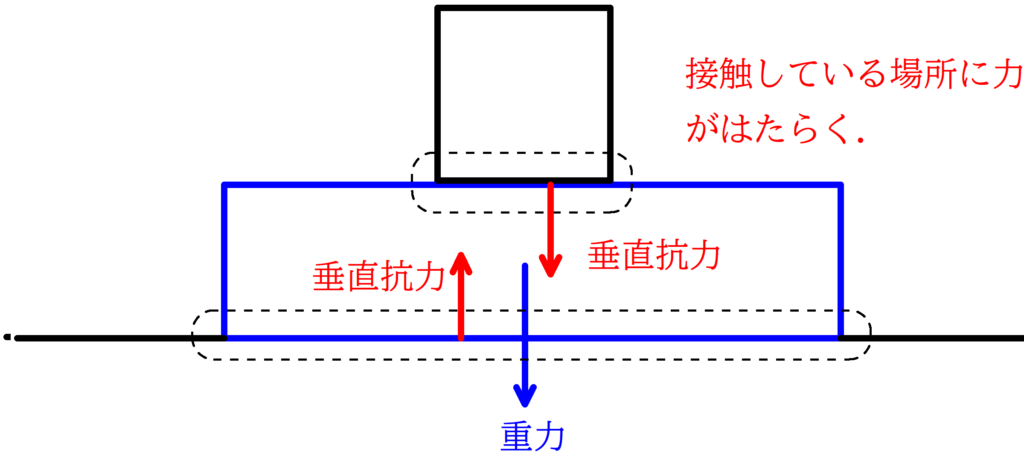
例:接触の相手によって,次のような力がはたらく.
面(床,物体,壁):垂直抗力と摩擦力
糸,ひも:張力
ばね:弾性力
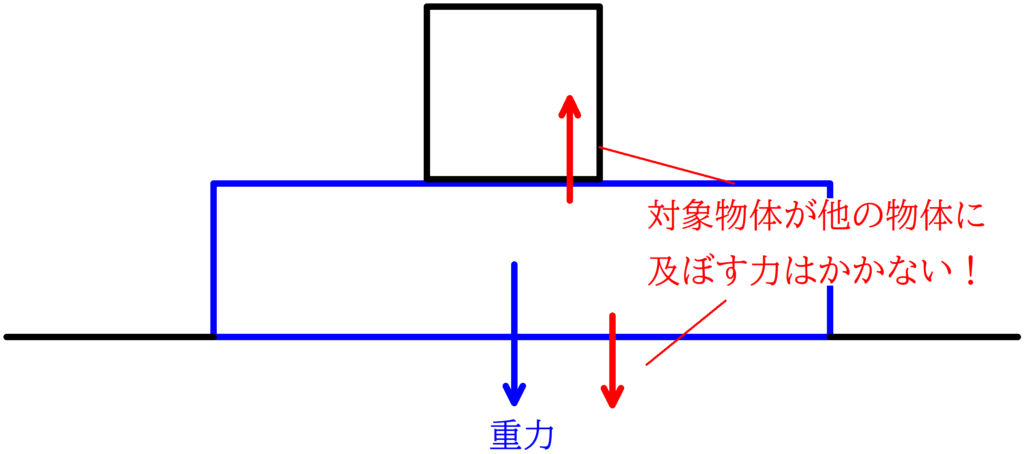
※ 注意:外から対象物体にはたらく力を書き込むのであって,対象物体が相手側に及ぼす力を対象物体にかかないようにする.
下はダメな図
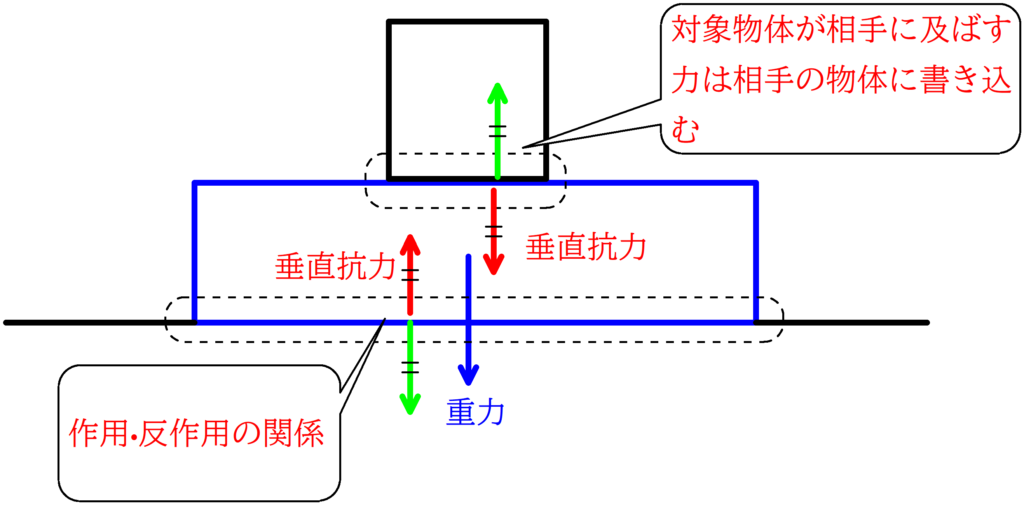
※ 勿論,対象物体が相手側に及ぼす力を相手の物体のところに図示するのはかまわない.
ただし,運動方程式やつり合いの式を立てる際には,あくまでも対象物体にはたらく力のみを式に入れる.
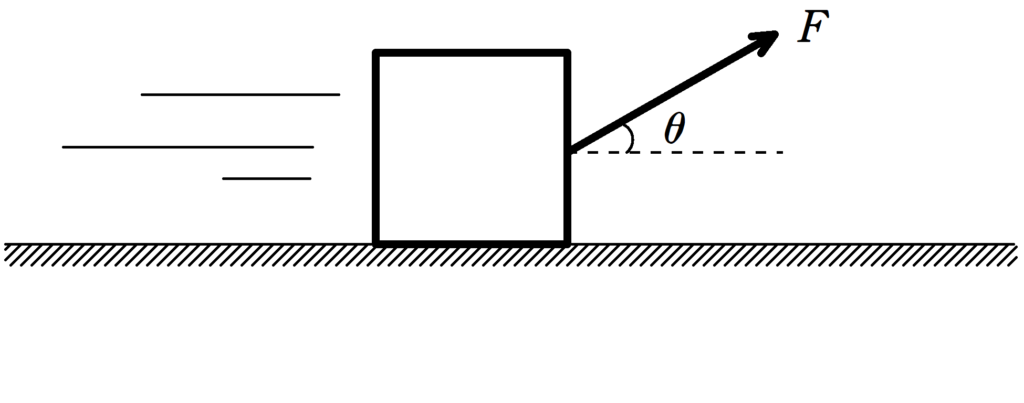
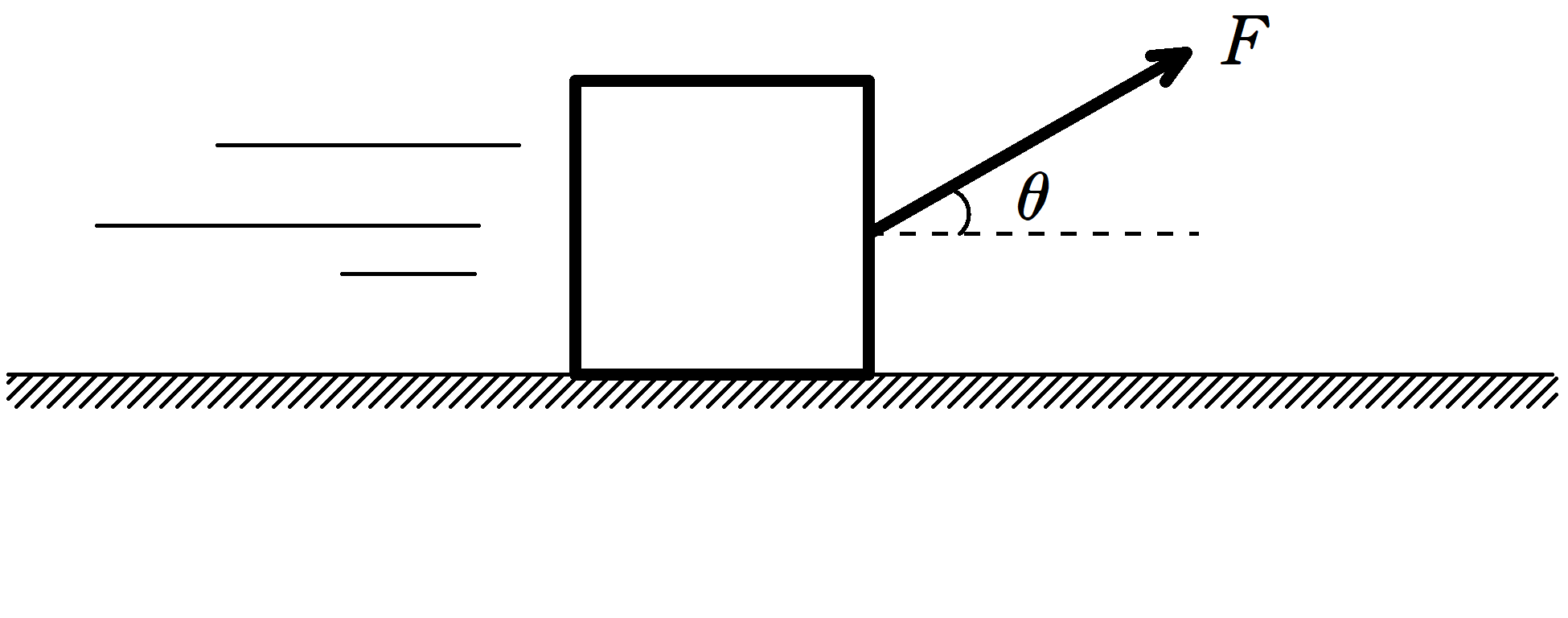
水平な床の上に質量$m$の物体をおき,水平からのなす角$\theta(0<\theta<\dfrac{\pi}{2})$の方向に一定の力$F$を加え続けたところ,物体は加速度運動をした.
床と物体の間の動摩擦係数を$\mu$,重力加速度の大きさを$g$とする.
このとき,物体の水平方向の加速度$a$を求めよ.
ただし,物体は床から浮かずに運動をする.
<解答>

「加速度を求めなさい」ということから,運動方程式を立てます.
そこで,床との垂直抗力の大きさを$N$として,力を図示しましょう!
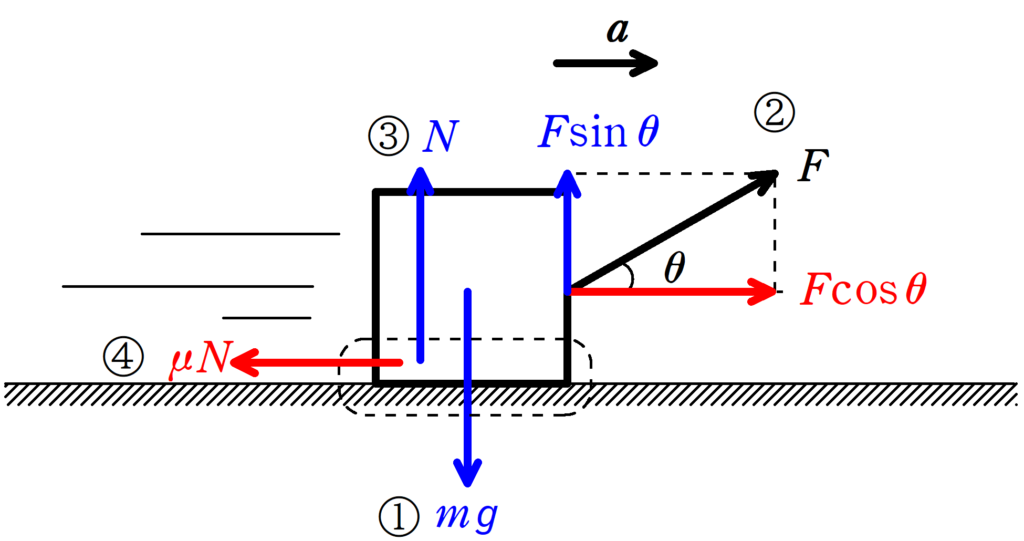
①:まずは重力をかく.
②:力$F$を水平方向と鉛直方向に分解する.
③④:接触面にはたらく垂直抗力$N$と動摩擦力$\mu N$をかく.
★ 鉛直方向のつり合いの式(青色の力のつり合い)
$N+F\sin\theta =mg$
$\therefore N=mg-F\sin\theta$ $\dots (\ast)$
★ 水平方向の運動方程式(右向きの加速度を$a$とする.)
$ma=F\cos\theta -\mu N$
$(\ast)$を代入して
$\eqalign{ma&=F\cos\theta -\mu(mg-F\sin\theta)\\&=F(\cos\theta +\mu \sin\theta)-\mu mg}$
$\therefore$ $a=\dfrac{F}{m}(\cos\theta +\mu \sin\theta)-g$

コメント
[…] [基礎編]運動方程式演習⑤ 動摩擦力を$mu mg$としては×NEKO今回は,動摩擦… […]