[演習]重心不変4

PHYさん

前回の内容はこちらです．

[演習]重心不変3

PHYさん 前回の内容はこちらです． 問題 図のように，水平でなめらかな床の上に質量$M_{3}$の三角台がおいてある．三角台の上面は傾角$\theta$の斜面でできており，斜面はなめらかである．斜面の上には質量$M_{2}$の物体Bが置か...

physicmath.net

2021.06.28

問題

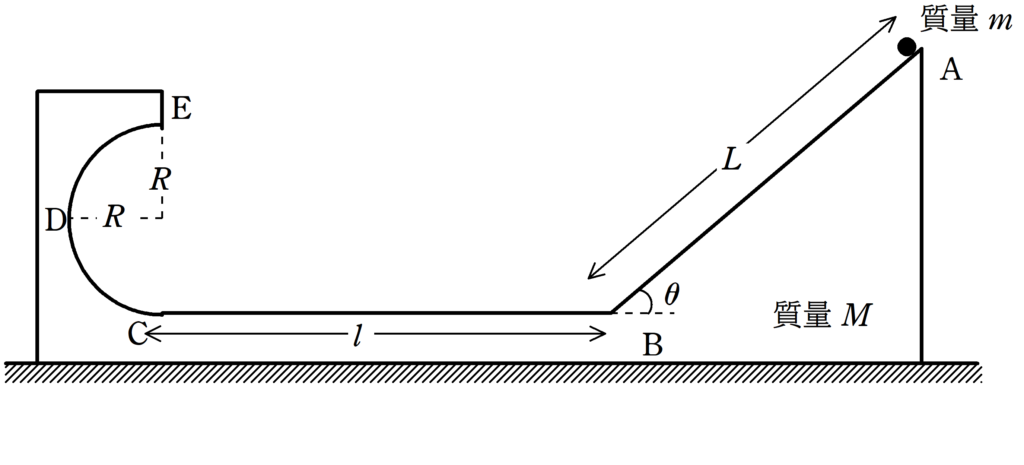
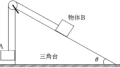
図のように，水平でなめらかな床の上に質量$M$の台がおかれている．台の上面は，傾角$\theta$で長さ$L$の斜面部分AB，長さ$l$の水平部分BC，半径$R$の曲面部分CDEからなっている．台を静止させた状態で質量$m$の大きさができる物体をAにおいて物体と台のおさえをはずしたところ，物体と台は運動を始めた．BおよびCはなめらかに接続されていて物体は台を離れることはないものとする．物体が台上のDに達したとき，台は床の上をどれだけ移動しているか．

＜解答＞

NEKO

今回も水平方向に関しては，台と物体にはたらく力の和が常に0だね．

NEKO

変位を利用した重心不変は次の２式を立てましょう．

★　重心不変の式

（図の左向きを正として）床から見た物体の水平方向の変位を$\varDelta x$，台の水平方向の変位を$\varDelta X$とする．重心不変の式より

$0=\dfrac{M\varDelta X+m\varDelta x}{M+m}$

$\varDelta x=-\dfrac{M}{m}\varDelta X$　$\dots (\ast)$

★　相対変位の式

下図を参考にして

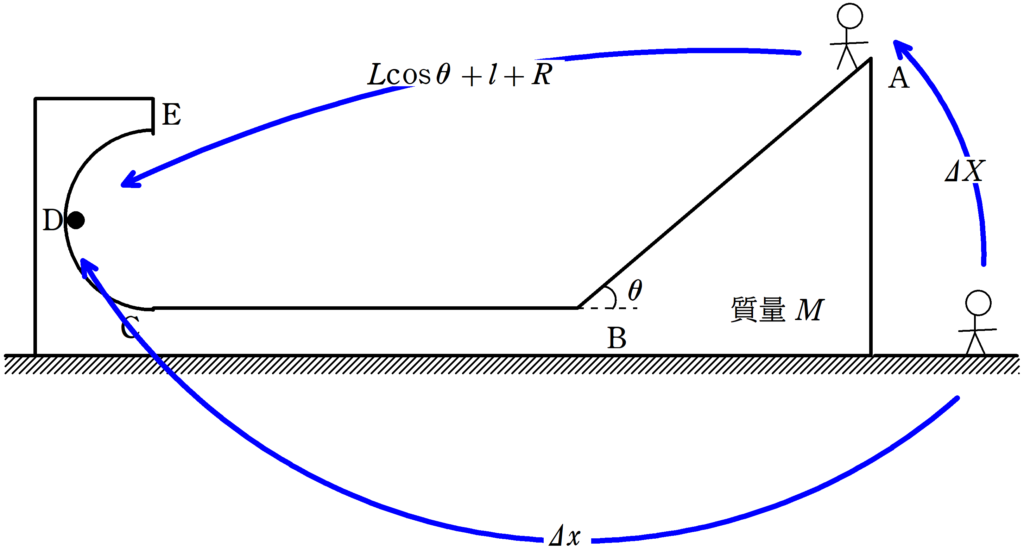
$\varDelta X+L\cos\theta+l+R=\varDelta x$　$\dots (2\ast)$

$(\ast)$，$(2\ast)$より

$\eqalign{\varDelta X+L\cos\theta+l+R&=-\dfrac{M}{m}\varDelta X\cr\dfrac{M+m}{m}\varDelta X&=-\left(L\cos\theta +l+R\right)\cr \varDelta X&=-\dfrac{m(L\cos\theta +l+R)}{M+m}}$

NEKO

したがって，台は図の右方向に$\dfrac{m(L\cos\theta +l+R)}{M+m}$(答)だけ移動するんだね．