
今回は苦手になりがちなドップラー効果の証明問題です.
次の問題を解きながら確認していきましょう.
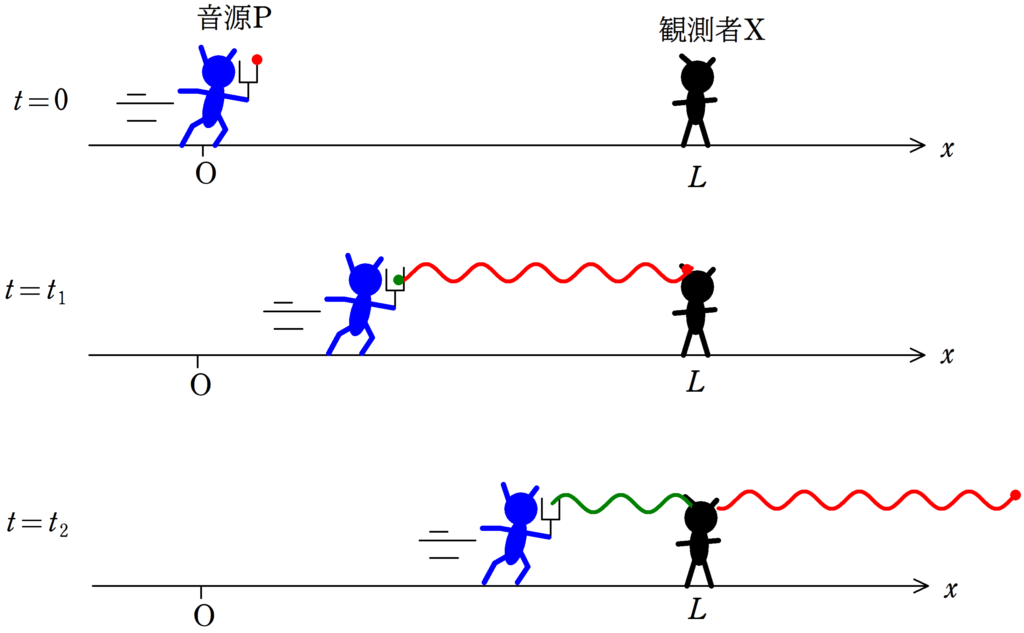
図のように,振動数$f_{0} [\rm Hz]$の音を出す音源$\rm P$が,$x$軸上を正の向きに速さ$v[\rm m/s]$で等速直線運動をしている.時刻$t=0 \rm s$において,音源$\rm P$が原点を通過したとする.
時刻$t=0 \rm s$に音源$\rm P$で作られた波が座標$x=L(>0)[\rm m]$で静止している観測者$\rm X$に伝わる時刻を$t=t_{1}[\rm s]$とし,時刻$t=t_{1}[\rm s]$に音源$\rm P$で作られた波が観測者$\rm X$に伝わる時刻を$t=t_{2}[\rm s]$とする.波の伝わる速さを$V[\rm m/s]$とするとき,次の問いに答えよ.ただし,風は吹いていないものとする.
(1) 時刻$t_{1}$を$L$,$V$を用いて表せ.
(2) 時刻$t_{2}$を$L$,$V$,$v$を用いて表せ.
(3) (1),(2)より,観測者が観測する振動数$f^{\prime}[\rm Hz]$を$V$,$v$,$f_{0}$を用いて表せ.
<解答>
(1)

時刻$t=0$において,作った波(上図の赤い点の部分)が静止している観測者$\rm X$に到達するまでの距離は$L$です.
音速が$V$なので,時刻$t_{1}$は
$t_{1}=\dfrac{L}{V}[\rm s]$ (答)
(2)

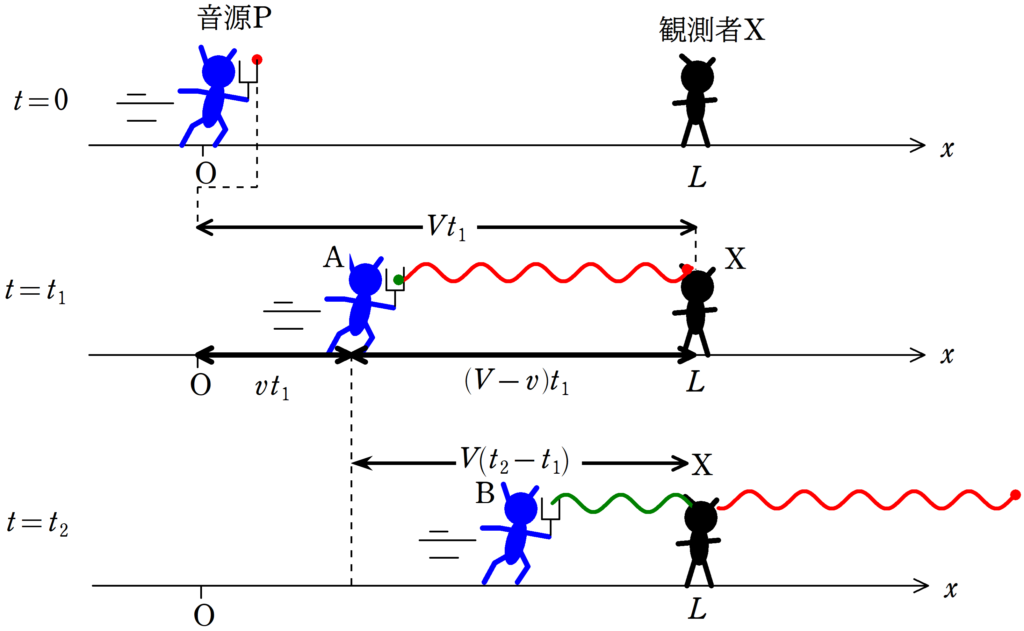
時刻$t=t_{1}$においては,音源$\rm P$は$vt_{1}$だけ移動しています.
また,$t=t_{1}$で発生した波(緑色の波)は$t=t_{1}$から$t=t_{2}$の間に波は,$V(t_{2}-t_{1})$だけ進みます.
そして,この距離は,$t=t_{1}$の図でかかれているように,$(V-v)t_{1}$と等しいです.
$\eqalign{V(t_{2}-t_{1})&=(V-v)t_{1}\cr t_{2}&=t_{1}+\dfrac{V-v}{V}t_{1}\cr t_{2}&=(1+\dfrac{V-v}{V})\cdot \dfrac{L}{V}}$
したがって,$t_{2}=(1+\dfrac{V-v}{V})\cdot \dfrac{L}{V} [\rm s]$(答)
(3)

さて,本題です.
音源の振動数と観測者が観測する振動数は次のように解釈しましょう.
★ 音源の振動数$[\rm Hz]$→1$\rm s$あたりに音源がつくる波の数
★ 観測者が観測する振動数$[\rm Hz]$→1$\rm s$あたりに観測者が受け取る波の数

そして,ドップラー効果の証明では,次の式をよく使います.
音源がつくった波の数だけ観測者は波を受け取る.
音源が振動数$f_{0}[\rm Hz]$の音を時間$t_{0}[\rm s]$だけつくったとする.
観測者が受け取る振動数を$f^{\prime}$,受け取る時間を$t^{\prime}$とすると,次の関係式が成り立つ.
$f_{0}t_{0}=f^{\prime}t^{\prime}$
(音源がつくる波の数=観測者が受け取る波の数)


観測者が上図の赤い波を受け取るときのことを考えるよ.
音源は赤い波を時間$t_{1}$の間で作ったので,音源がつくった波の数は
$f_{0}t_{1}$ $\dots (\ast)$
一方,音源はこの赤い波を時間$t_{2}-t_{1}$の間で受け取っています.
なので,観測者が観測する振動数を$f^{\prime}$とすると,観測者が受け取る波の数は
$f^{\prime}(t_{2}-t_{1})$ $\dots (2\ast)$
音源がつくった波の数=観測者が受け取る波の数
であるから,$(\ast)$と$(2\ast)$より
$f_{0}t_{1}=f^{\prime}(t_{2}-t_{1})$ $\dots \clubsuit$
(1)と(2)より
$t_{1}=\dfrac{L}{V}$
$t_{2}-t_{1}=\dfrac{V-v}{V}\cdot \dfrac{L}{V}$
を$\clubsuit$に代入して
$f_{0}\cdot \dfrac{L}{V}=f^{\prime}\cdot \dfrac{V-v}{V}\cdot \dfrac{L}{V}$
$\therefore f^{\prime}=\dfrac{V}{V-v}f_{0}[\rm Hz]$ (答)



コメント
[…] […]
[…] こちらは基本問題 […]
[…] ドップラー効果の証明問題 […]