
前回までは,
導体棒が磁場中を動く→電池になる
ことを確認してきました.
前回の内容です.
PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は,PQの長さを$l$,PQ方向に垂直な速さを$v_{\perp}$,導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば,
$V=v_{\perp}Bl$

今回は,導体棒を使って回路の問題を解きたいと思います.
そこで,導体棒の問題で立てて欲しい3つの式を紹介します.
- 回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
- 導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
- 導体棒と回路の系全体のエネルギー収支の式
<説明>
1.回路の式(オームの法則,コンデンサーの基本式,電荷保存則など)
導体棒が磁場中を動くと電池になるので,回路の問題として考えてください.抵抗だけあれば,オームの法則,より複雑な回路になったらキルヒホッフの法則を立てます.
コンデンサーがある場合は電荷保存の式を立てることもあります.要するに普通の回路の問題としてとらえるということです.
2.導体棒の運動に関する式(つり合いの式,運動方程式,運動量保存則など)
導体棒の運動を力学の問題としてとらえてください.つり合っていれば,つり合いの式を立てればいいし,運動していれば,運動方程式を立てて,加速度を求め,どのような運動かを求めることで問題の解決に向かいます.
3.導体棒と回路の系全体のエネルギー収支の式
エネルギー収支の式を立てる際には注意が必要です.
普通,導体棒に電流が流れることではたらく電磁力の仕事や,誘導起電力がする仕事はいれません.
これは,電磁力がした仕事+誘導起電力がする仕事=0になるからですが,詳しくは,こちらをみてください.

それでは,3つの式を意識して問題を解いてみましょう.
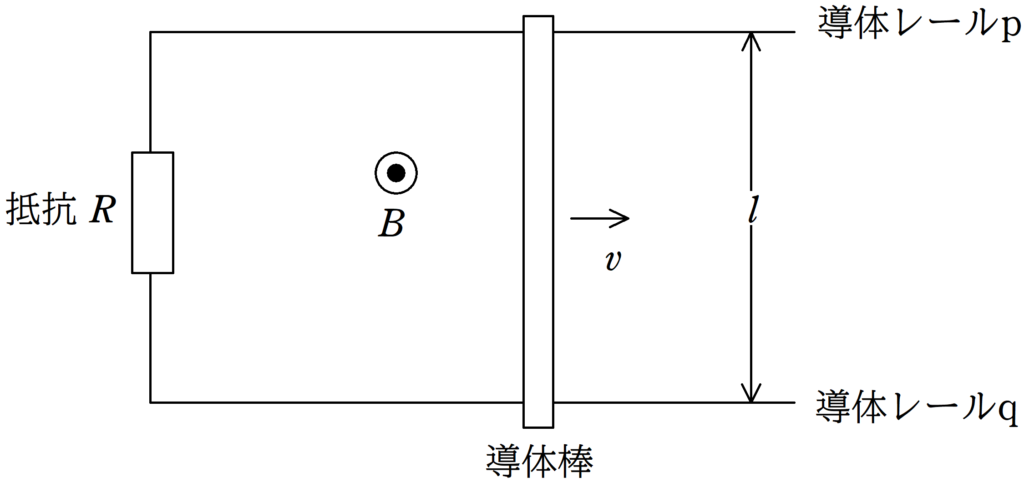
図のように,平行に固定された導体レールp,qと抵抗値$R$の抵抗と長さ$l$の導体棒を用いて回路をつくった.
いま,画面奥から手前向きに一様な磁束密度$B$の磁場をかけた状態で導体棒を右方向に速さ$v$で等速直線運動させた.
抵抗値$R$以外の抵抗は無視をし,摩擦や空気抵抗も無視をする.
(1) 導体棒に流れる電流の大きさを求めよ.
(2) 導体棒を等速度運動させるために外力を加えている.この外力の大きさと向きを答えよ.
(3) 抵抗で単位時間あたりに生じるジュール熱を求めよ.
(1) 導体棒が磁場中を速さ$v$で動いているので起電力$vBl$の電池になります.
すなわち,下図のような回路ができます.
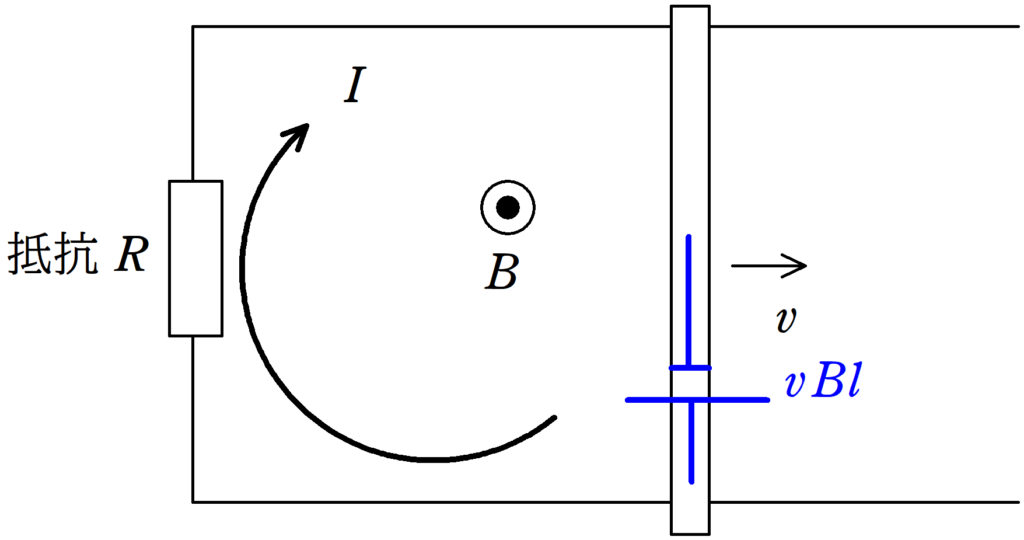
回路に流れる電流を$I$とします.オームの法則より
$vBl=RI$ $\therefore I=\dfrac{vBl}{R}$
したがって,導体棒に流れる電流の大きさは$\dfrac{vBl}{R}$です.向きは導体棒の上側から下側へ向かう向きです.
(2) 磁場中を電流が流れる→電磁力がはたらきます.
電磁力の大きさ$F$は
$F=IBl=\dfrac{vB^{2}l^{2}}{R}$
です.
電磁力はフレミング左手の法則で決まります.(左手の親指が力,人差し指が磁場,中指が電流)
すると,電磁力は図の左方向にはたらくことを確認できます.
導体棒が動いている方向と逆方向ですね.
つまり,電磁力しかはたらかないと,導体棒はだんだんと速度を落とし,最終的には静止してしまいます.
それを阻止するために,外力が電磁力と逆方向である右向きに同じ大きさの力$\dfrac{vB^{2}l^{2}}{R}$を加えます.
(3) 最後に,単位時間あたりに生じるジュール熱を2通りに紹介します.
・単位時間あたりに抵抗で消費するジュール熱の式を用いる.
抵抗にかかる電圧を$V$,流れる電流を$I$とすると,単位時間あたりに抵抗で消費するジュール熱$P_{1}$は
$P_{1}=VI=vBl\cdot \dfrac{vBl}{R}=\dfrac{(vBl)^2}{R}$
・導体棒にはたらく外力の仕事率=単位時間あたりに抵抗で消費するジュール熱の式を立てる.
エネルギー収支の式です.導体棒は運動エネルギーも位置エネルギーも変化していません.
なので,導体棒にはたらく外力がする仕事率がそのまま単位時間あたりのジュール熱となります.
外力がする仕事率$P_{2}$は
$P_{2}=Fv=\dfrac{(vBl)^2}{R}$

(今回は)直接ジュール熱を計算することもできるし,エネルギー収支の式からも計算ができるんだね.
3つの式を意識できたでしょうか?
今回は,導体棒の基本の基本でした.
これから少しずつ難しくなっていきます!
次回の内容はこちら.




コメント
[…] […]
[…] […]
[…] […]