
波動や交流の問題で,やたら”位相”という言葉がでてくるんだけど,一体どういう意味?

単振動の式
$y=A\sin(\omega t+\phi)$
の$\omega t+\phi$部分を位相と言います.
とは言ってもイメージがわかないので,今回は順を追って位相について説明していきましょう.
単振動は等速円運動する物体の影の運動

単振動って,等速円運動の影の運動だったよね.

はい.
下図のように,青い物体が等速円運動しているとします.
そこに,左側から光を当てると,青い物体の影がスクリーンにうつります.
この運動が単振動になっています.
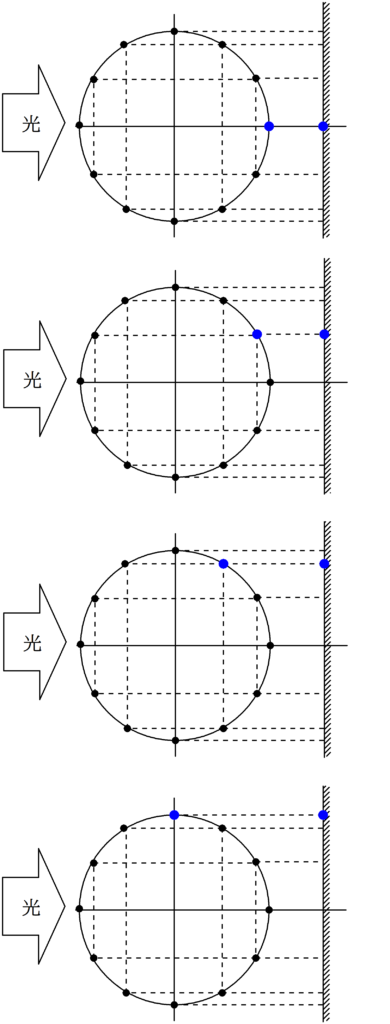
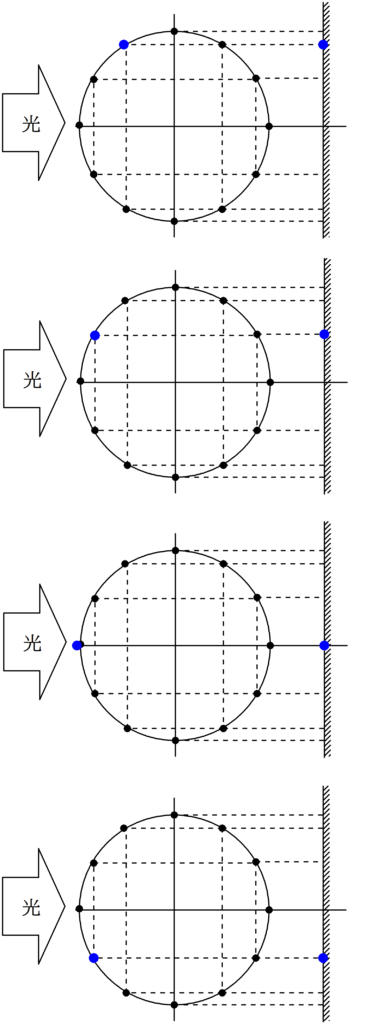

青い物体が反時計回りに等速円運動すると,その影が上下に振動している様子がわかるね.

そして,物体が角速度$\omega$で回転しているとき,時間$t$で$\omega t$回転します.
このときの物体の影の座標は
$A\sin \omega t$
となります.(スタート地点にとまわる方向によって形は異なります.)
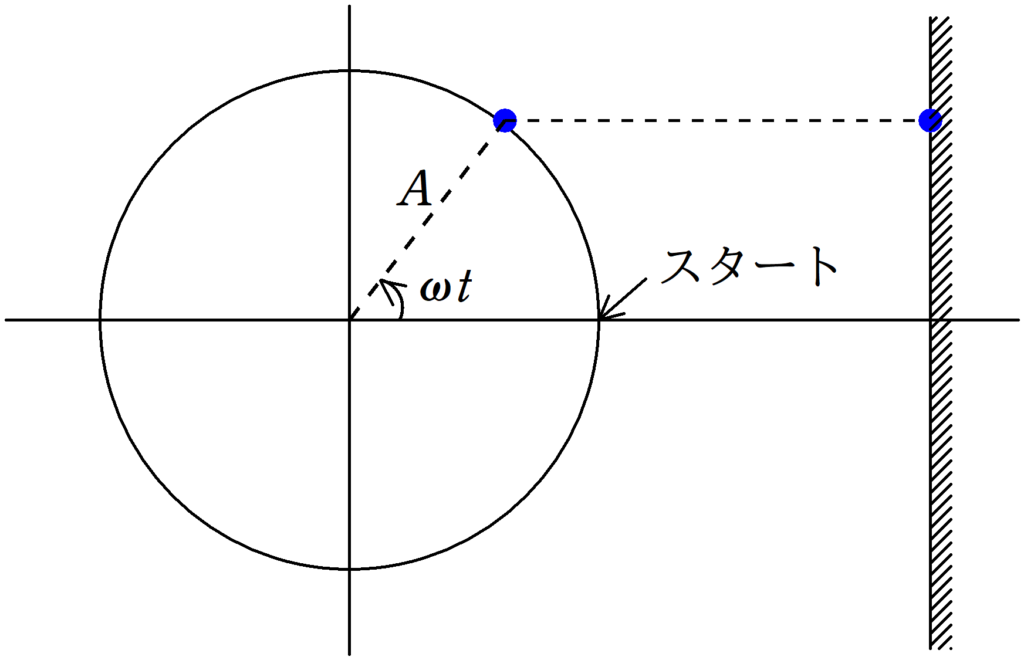

つまり,$\sin$や$\cos$の中の部分が位相ってわけだね.
位相差とは?

波動や交流では,”位相”というより,”位相差”が出てくるんだよね.あと,同位相とか逆位相とか..

2つの以上の振動が出てくるときに,位相差を考えることができます.
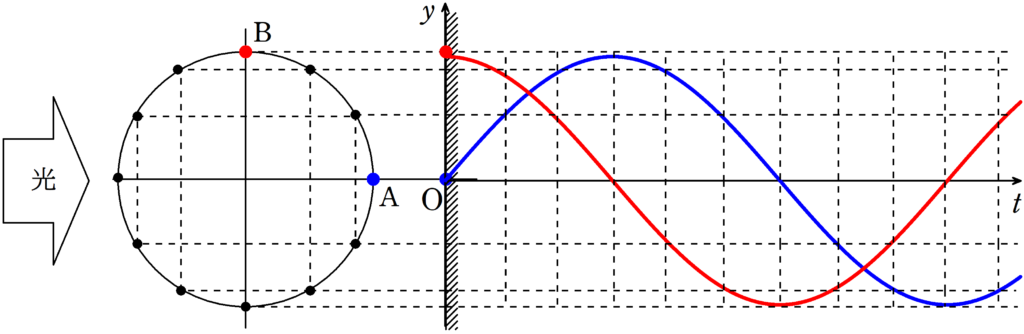
Aからスタートする青の物体とBからスタートする赤の物体が反時計回りに等速円運動しているとします.
ここに,同じく,左側から光を当てて影の運動を観察します.
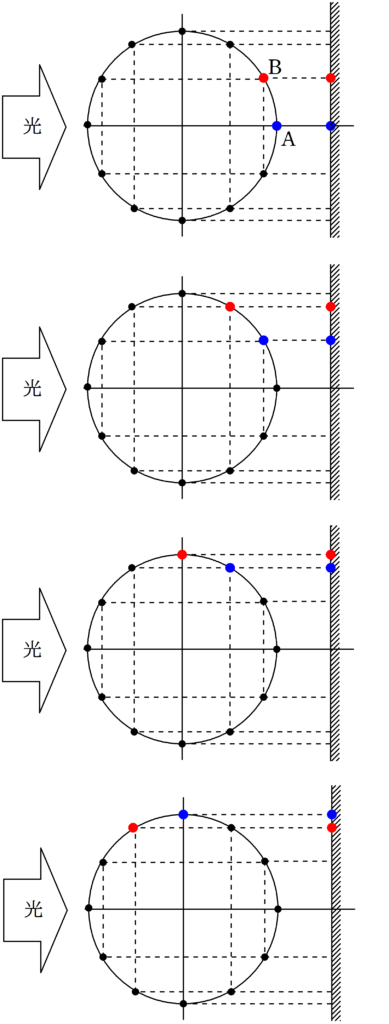
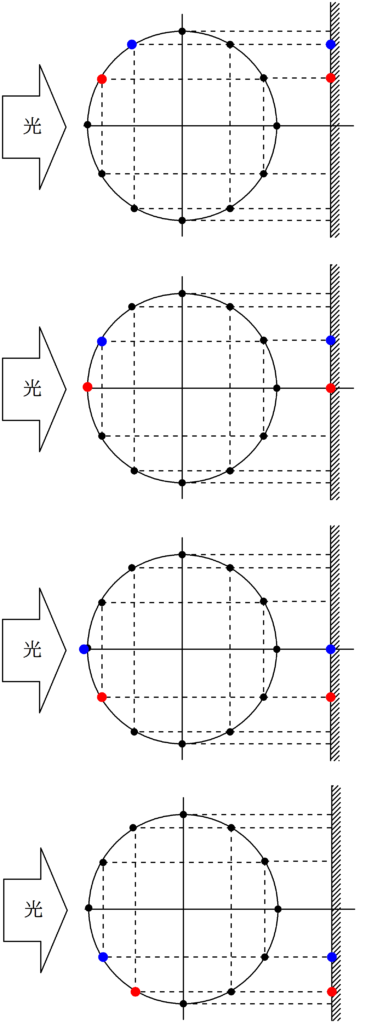

青い物体が常に赤い物体を追いかけているね!
影の運動も青い物体が赤い物体を追いかけている.

そうです.
このとき,
赤い物体の振動の位相は青い物体の振動の位相より進んでいる
とも言えますし,
青い物体の振動の位相は赤い物体の振動の位相より遅れている
とも言えます.(位相差$\phi$を$0\leqq \phi\leqq \pi$としています.)

確かに,赤い方の物体の振動は青い物体より先だよね.

次に,振動の時間変化をみていきましょう.
縦軸が媒質の変位(媒質が今現在どこにいるか),横軸が時間です.
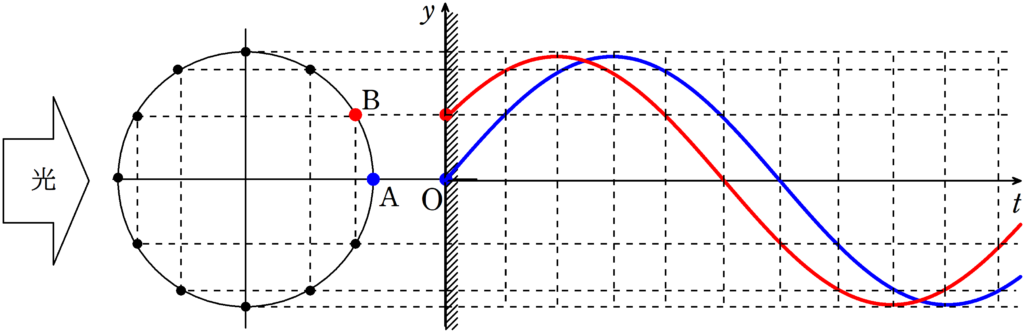

上図は,赤の方が常に$\dfrac{\pi}{6}$先にいますね.
なので,
赤の位相が青よりも$\dfrac{\pi}{6}$進んでいる
です.または,青の方が赤よりも常に$\dfrac{\pi}{6}$後にいるので
青の位相が赤よりも$\dfrac{\pi}{6}$遅れている
と言えます.

グラフだけ見ると,ついつい青の方が進んでいると思っちゃうんだよね!
実際,よく考えてみると,赤の方が先に振動しているのに・・・.

そうですね,その手の間違いはよく見かけます.
では,青の媒質の振動と赤の媒質の振動の式は,振幅を$A$,角振動数を$\omega$とすると,それぞれどのように表されるでしょうか?

青の媒質の振動は
$y_{青}=A\sin \omega t$
だね.赤い方は常に,青より位相(角度部分)が$\dfrac{\pi}{6}$進んでいるだから
$y_{赤}=A\sin(\omega t +\dfrac{\pi}{6})$
だね.
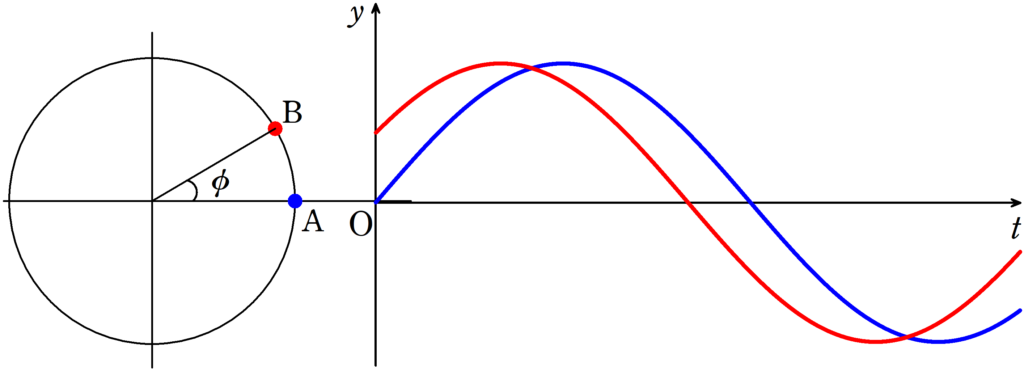
上図において,青の物体の振動の位相と赤の物体の位相差を$\phi(0\leqq \phi\leqq\pi)$とする.
このとき,次のことが言える.
- 赤は青よりも位相が$\phi$進んでいる.
- 青は赤よりも位相が$\phi$遅れている.
また,グラフから位相の進み遅れを読み取るときは,青の位相が進んでいると勘違いする人が多いので注意.実際は,赤の方が先に振動しているため,赤の方が位相が$\phi$進んでいる.
振幅を$A$,角振動数$\omega$とすると,時刻$t$における媒質の座標$y_{青}$,$y_{赤}$はそれぞれ
$y_{青}=A\sin \omega t$
$y_{赤}=A\sin(\omega t+\phi)$
演習問題

では,最後に演習問題で確認しましょう.
(1)
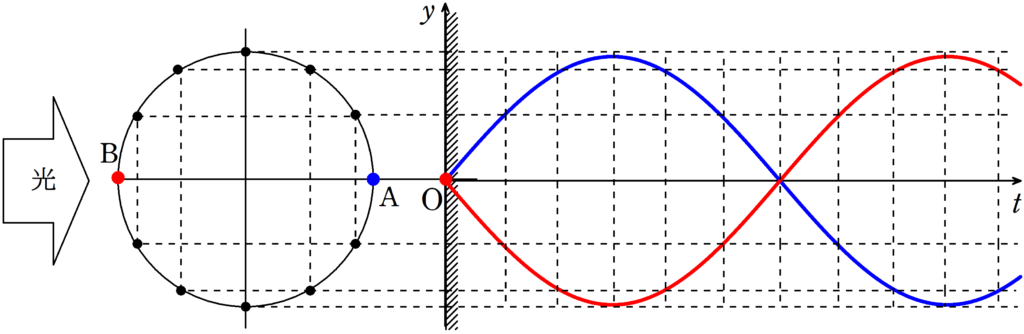
上図において,青の媒質と赤の媒質の位相差$\phi(0\leqq \phi \leqq\pi)$はどれだけか.
(2) $A$,角振動数$\omega$とする.時刻$t$において2つの媒質A,Bにおける振動の式が
$y_{\rm{A}}=A\sin \omega t$
$y_{\rm{B}}=A\cos\omega t$
であった.位相差を$\phi(0\leqq \phi \leqq\pi)$とするとき,AとBの位相差$\phi$を求めよ.また,どちらの方が位相が進んでいるか答えよ.
<解答>
(1) 位相差は$\pi$です.この問題からはどちらの位相が進んでいるかはわかりません.
実際の問題でも位相差が$\pi$ずれる場合はどちらがの位相が進んでいるとは聞かれないでしょう.
グラフを見れば,赤と青は常に真逆の振動に振動をしています.これを逆位相ともいいます.
反対に位相差が0の振動を同位相といいます.
(2) $\omega t$の部分が同じだから位相差は$0$,では×です.
$\sin$または$\cos$に合わせて比べてあげましょう.
$y_{\rm{B}}=A\cos\omega t=A\sin(\omega t +\dfrac{\pi}{2})$
とすれば,$y_{\rm{A}}=A\sin \omega t$と比べて
Bの方がAより位相が$\dfrac{\pi}{2}$進んでいる.
(Aの方がBより位相が$\dfrac{\pi}{2}$遅れている.)
ちなみに,
$y_{\rm{A}}=A\sin \omega t=A\cos(\omega t -\dfrac{\pi}{2})$と変形して比べることもできます.
グラフをみると次のようになります.

位相がわかってきたら,波動の干渉問題や交流の問題を解いて理解を深めましょう!



コメント
[…] […]
[…] […]
[…] 位相って何!?[高校物理] […]
[…] […]
[…] ・「位相」についてよくわからない人は「位相ってなに?」 […]
[…] ・「位相」についてよくわからない人は「位相ってなに?」 […]