twitterの問題2の解答

訂正：Pに対する小球に与える速度の大きさは飛行物体Pの速度の大きさと同じです．

＜解答＞

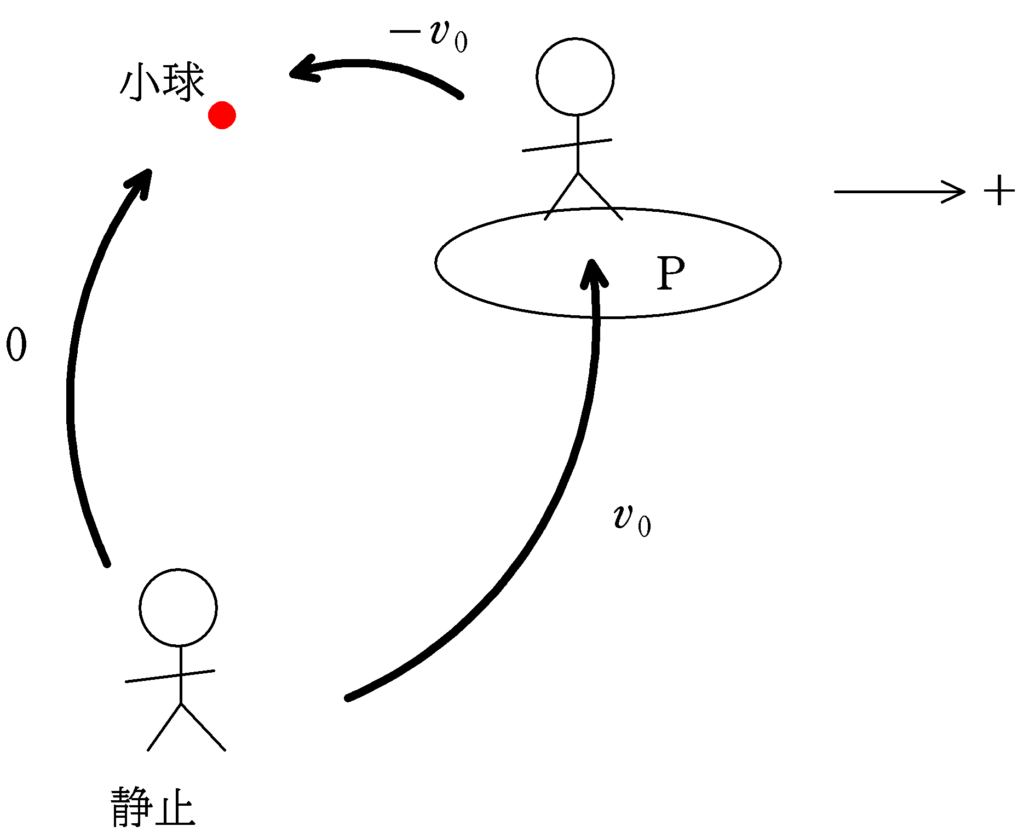
静止している人からみた小球の初速度は$0$なので，各小球は自由落下する．

時刻$0$で飛行物体Pが原点を通過し，このときに小球を投げ出したとする．時間$t_{0}$ごとに小球を自由落下させるため，下図のように，Pの移動する方向に$x$座標，鉛直下向きに$y$座標をとると，各小球の$x$座標は$v_{0}t_{0}，2v_{0}t_{0}，3v_{0}t_{0}，\cdots ，nv_{0}t_{0}，\cdots$である．

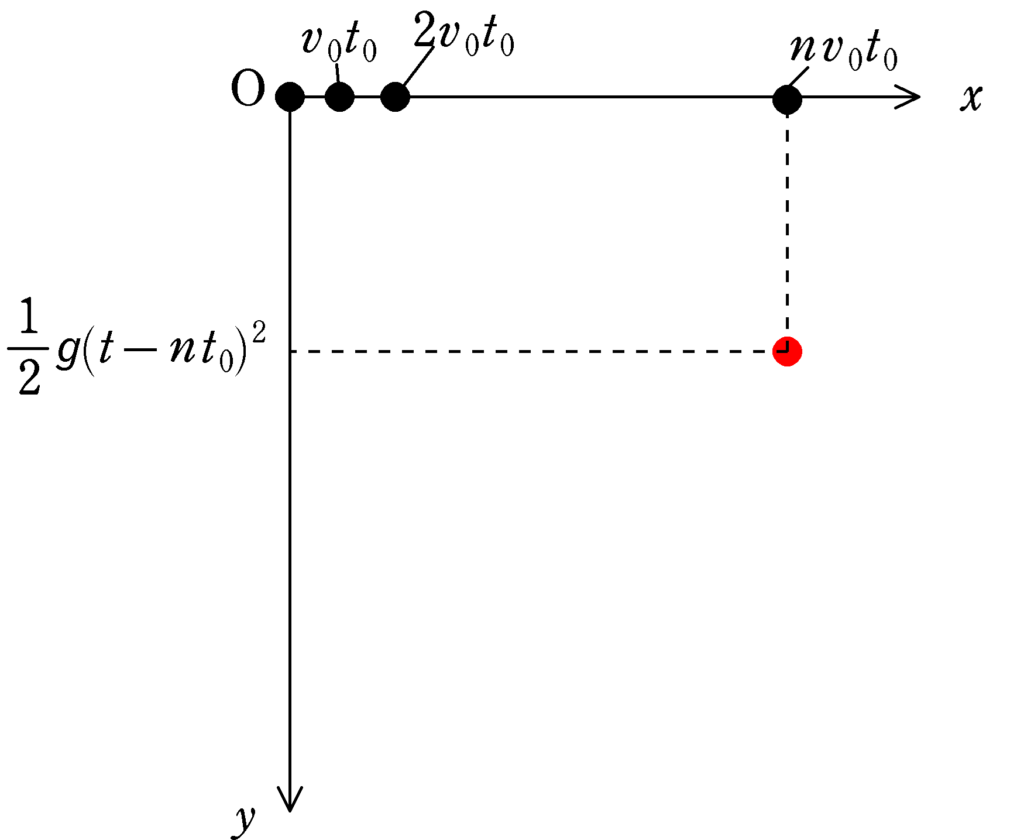
原点で投げ出した小球の時刻$t$での$y$座標$y_{0}$は，

$y_{0}=\dfrac{1}{2}gt^{2}$

$x_{1}=v_{0}t_{0}$で投げ出した小球は原点より，$t_{0}$だけ遅れて投げ出しているので，時刻$t$での$y$座標$y_{1}$は

$y_{1}=\dfrac{1}{2}g(t-t_{0})^{2}$

$x_{2}=2v_{0}t_{0}$で投げ出した小球は原点より，$2t_{0}$だけ遅れて投げ出しているので，時刻$t$での$y$座標$y_{2}$は

$y_{2}=\dfrac{1}{2}g(t-2t_{0})^{2}$

となる．一般的に$0$以上の整数$n$について，$x_{n}=nv_{0}t_{0}$で投げ出した小球は原点より，$nt_{0}$だけ遅れて投げ出しているので，時刻$t$での$y$座標$y_{n}$は

$y_{n}=\dfrac{1}{2}g(t-nt_{0})^{2}$

そこで，

$x_{n}=nv_{0}t_{0}　\cdots (\ast)$と$y_{n}=\dfrac{1}{2}g(t-nt_{0})^{2}　\cdots (2\ast)$から，$n$を消去した$x_{n}$と$y_{n}$の関係を求める．

$(\ast)$から，$nt_{0}=\dfrac{x_{n}}{v_{0}}$として，$(2\ast)$に代入すると

$y_{n}=\dfrac{1}{2}g\left(t-\dfrac{x_{n}}{v_{0}}\right)^{2}=\dfrac{1}{2v_{0}^{2}}\left(x-v_{0}t\right)^{2}$　$\cdots (3\ast)$

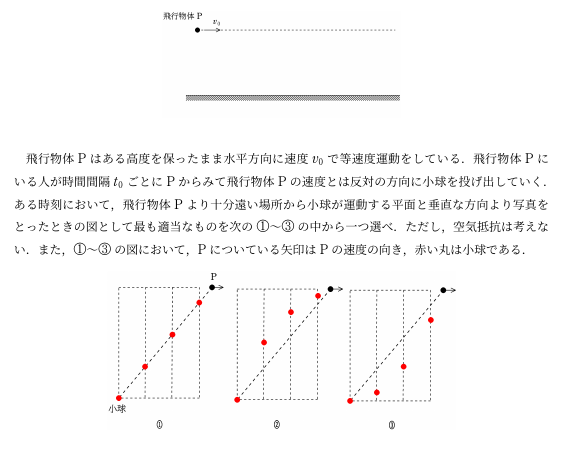
選択肢の図は，$t$を固定した「写真」である．そこで，$(3\ast)$式での$t$を定数とみてグラフを考えると，放物線であることがわかり，その頂点は$(v_{0}t，0)$である．以上のこと踏まえて，最も適当なものは②