
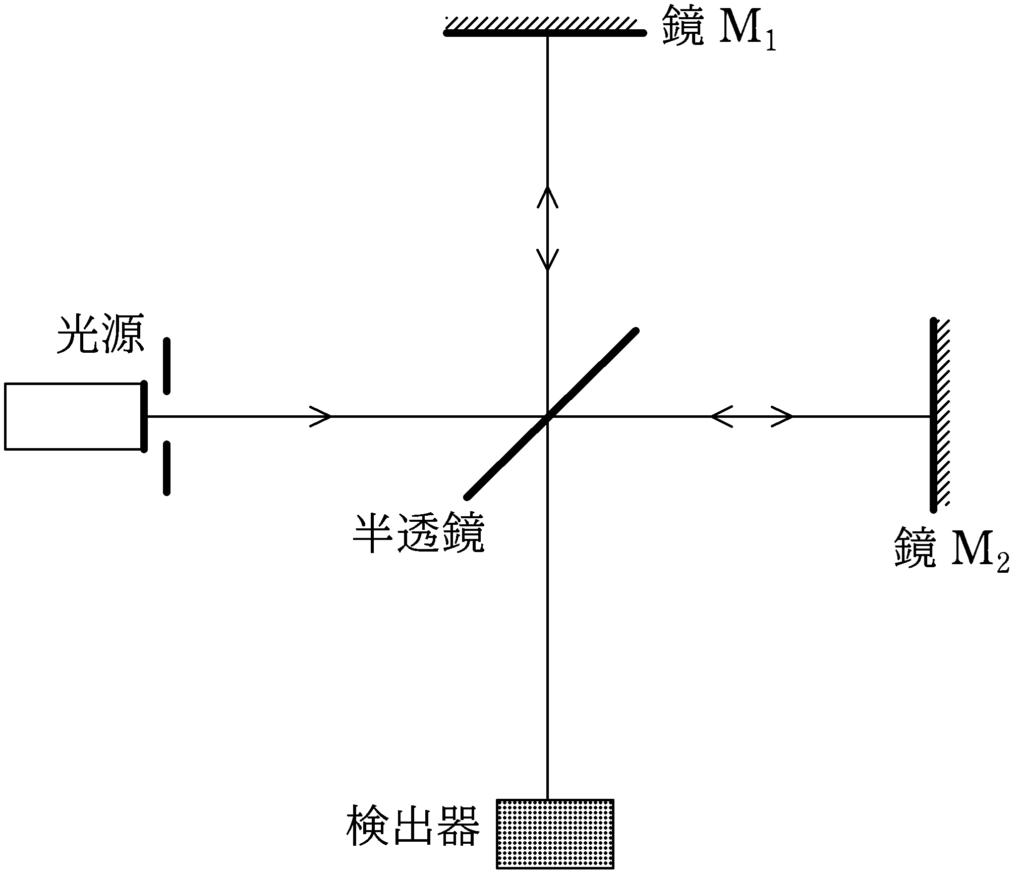
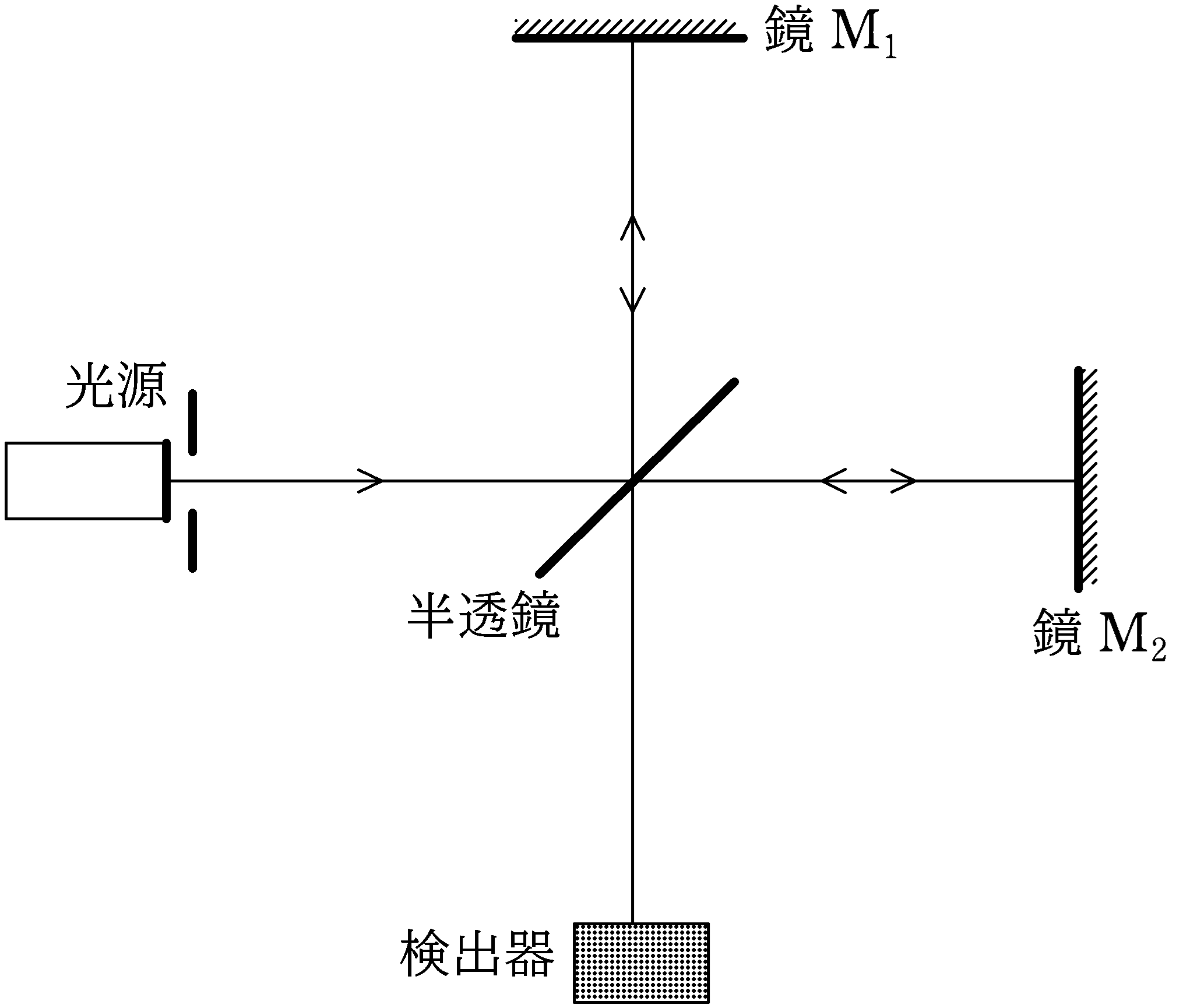
図のような干渉計が空気中におかれている.光源から出て進む単色光が,入射光線に対して,$45^{\circ}$傾けた半透鏡(ハーフミラー)に達し,一部は反射し,残りは透過する.このうち,半透鏡で反射したのち,鏡$\rm M_{1}$で反射した後,半透鏡を透過して検出器に至る光線をaとする.一方,半透鏡を透過し,鏡$\rm M_{2}$で反射した後,半透鏡で反射して検出器に至る光線をbとする.
鏡$\rm M_{1}$は固定されているが,鏡$\rm M_{2}$は光線bの経路と平行な方向に動かすことができる.はじめ,光線aと光線bの光路差は0になるように調整してある.空気の光線の波長を$\lambda_{0}$とし,空気の屈折率を$1.0$とする.
鏡$\rm M_{2}$をはじめの状態からゆっくりと半透鏡から遠ざかるように動かしたろころ,検出器にて観測される光の強度が極大と極小をくり返した.光の強度が極大になってから,次にはじめて極小になるまでに鏡$\rm M_{2}$の移動した距離を$\lambda_{0}$を用いて表せ.

干渉による位相差の条件をまとめると次のようになります.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$

今回は距離の差による位相のずれのみを考えればよいね.
何度か反射はしているけど,光線aも光線bも同じ回数反射しているから,反射による位相差はなしでよいでしょう.
そもそも位相差とは何かをもう一度考えていきましょう.
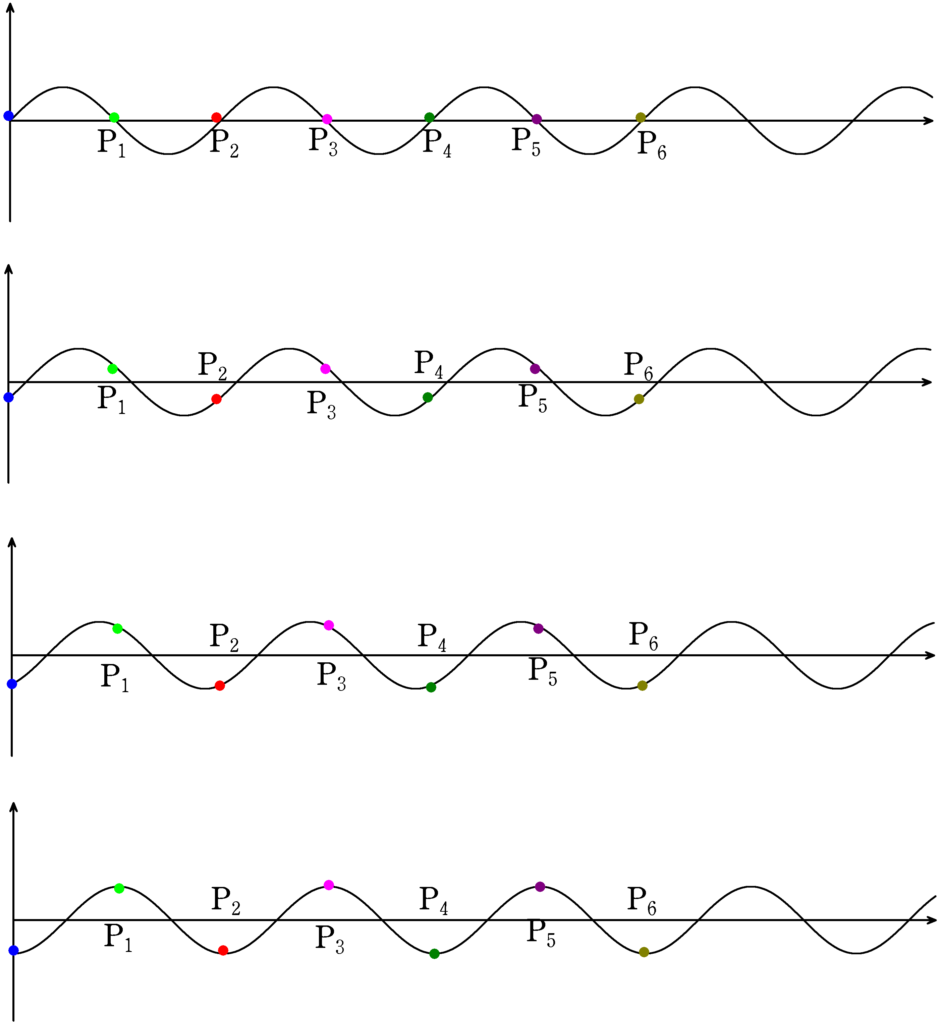

上図は,波が右方向に進行している様子を表しています.
青の媒質を基準とすると,$\rm P_{1}$は$\pi$,$\rm P_{2}$は$2\pi$,$\rm P_{3}$は$3\pi$,$\rm P_{4}$は$4\pi$,$\rm P_{5}$は$5\pi$,$\rm P_{6}$は$\rm 6\pi$,$\rm P_{7}$は$7\pi$の位相のずれがあります.
位相差が$2\pi,4\pi,6\pi$の媒質である$\rm P_{2},P_{4},P_{6}$は,媒質のタイミングが一緒なんだね.距離が離れると位相差が大きくなるんだね.
さらに, 位相差が$\pi,3\pi,5\pi,7\pi$の媒質である$\rm P_{1},P_{3},P_{5},P_{7}$は,媒質が真反対になるんだね.

たとえば,検出器において,光線aと光線bの位相差が$30\pi$だとしましょう.このとき,振動のタイミングが一緒なので,強め合います.
光線bを半透鏡から少しずつ遠ざけると,光線aとの位相差は少しずつ大きくなっていくね.
すると,位相差が$31\pi$になったときにタイミングが真反対になって弱め合います.
つまり位相差が$\pi$分ずれたときに,強め合いから弱め合いに変わるんだね.
今回は,光の強度が極大(強め合い)から極小(弱め合い)になるときのことを考えているので,位相差が$\pi$分ずれたときのことを考えます.
鏡$\rm M_{2}$を移動させた距離を$\varDelta x$とすると,往復分を考えて$2\varDelta x$分の行路差が増えます.すると,位相差は
$\dfrac{2\pi}{\lambda_{0}}\times 2\varDelta x$
分だけ変化します.これが$\pi$になるので
$\dfrac{2\pi}{\lambda_{0}}\times 2\varDelta x=\pi$
$\therefore \varDelta x=\dfrac{\lambda_{0}}{4}$ (答)


コメント
[…] マイケルソン干渉計演習1PHYさん今回から「マイケルソン干渉計」の問題を… 問題 […]