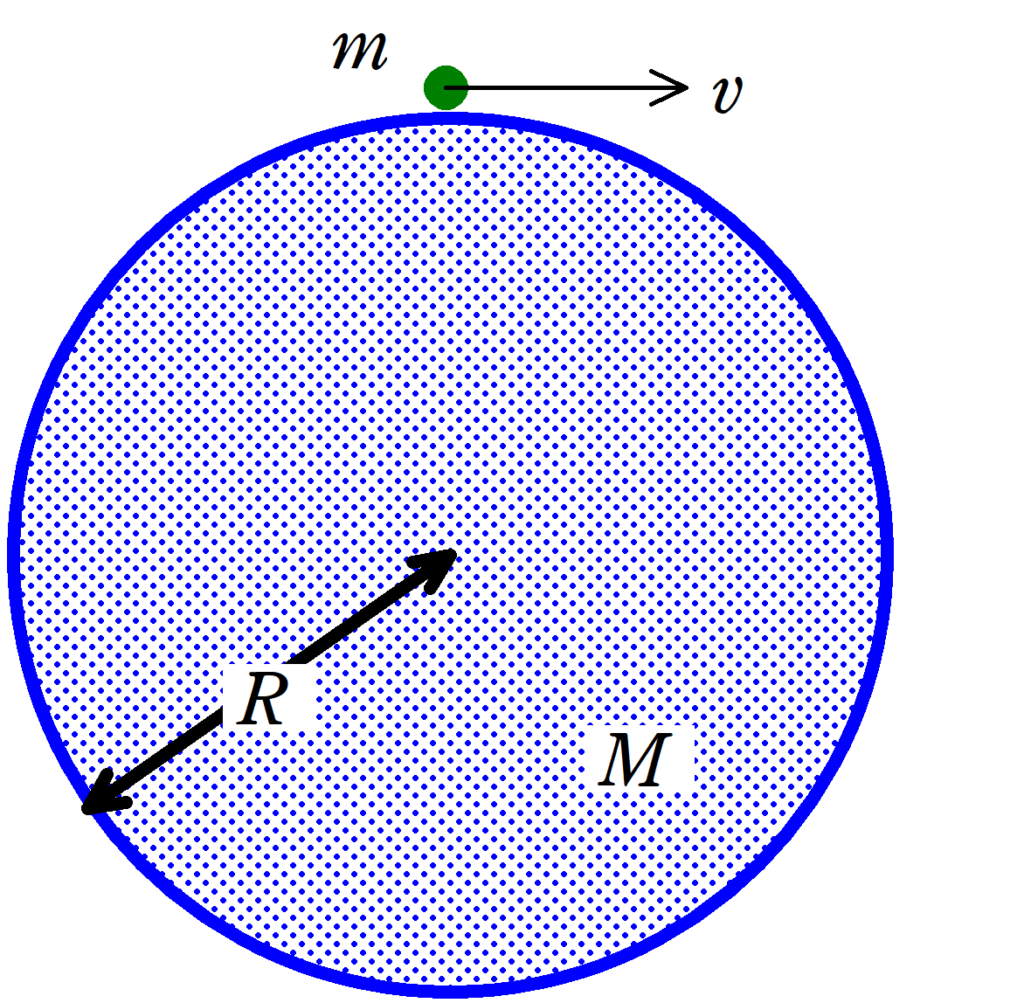
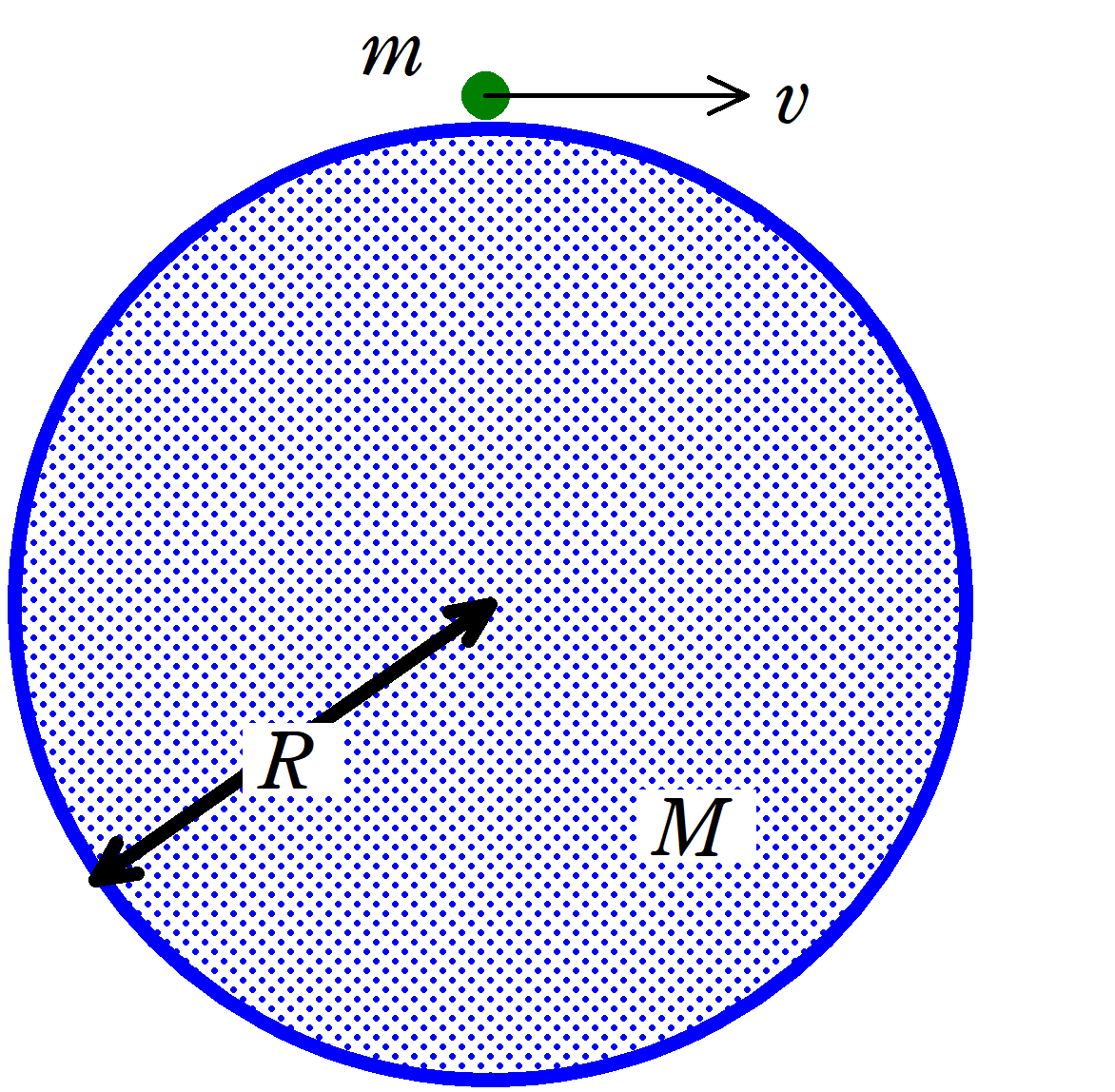
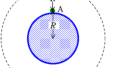
[演習]万有引力の問題2 宇宙速度 | Physicmath（フィジクマス）

問題

上図のように質量$M$で半径$R$の惑星Aがある．惑星Aの自転の影響は無視をする．惑星Ａの表面上に質量$m$の物体があり，この物体に与える初速度によって，物体は様々な軌道を描く．万有引力定数を$G$として次の問いに答えよ．ただし，空気抵抗は考えないものとする．

(1)　惑星Ａの表面での重力加速度の大きさは$g$であった．$g$を$G$，$R$，$M$を用いて表せ．

(2)　物体に初速度$v_{1}$を水平方向に与えたところ，物体は半径$R$の円運動をした．このとき，$v_{1}$を$g$，$R$を用いて表せ．

(3)　物体に初速度を与えたところ，物体は無限遠に到達した．このとき，与えた初速度の大きさの最低値$v_{2}$を$g$，$R$を用いて表せ．

＜解答＞

(1)

NEKO

万有引力の大きさは次のようになります．

万有引力

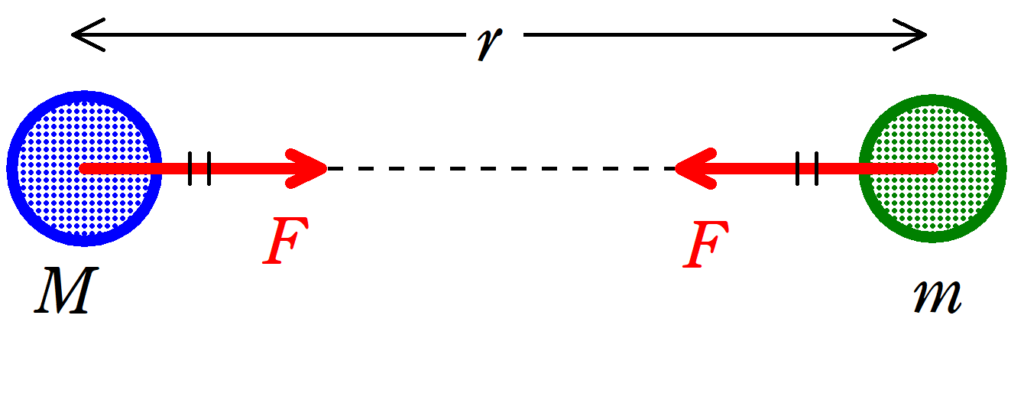
質量$M$の物体と質量$m$の物体の重心間の距離を$r$とする．万有引力定数を$G$とするとき，万有引力の大きさ$F$は

$F=G\dfrac{Mm}{r^{2}}$

$G$とgの関係

半径$R$で質量$M$の惑星の表面上の重力加速度の大きさを$g$とする．

惑星の自転の影響を無視するとき，重力加速度の大きさ$g$と万有引力定数$G$には次の関係がある．

$gR^{2}=GM$

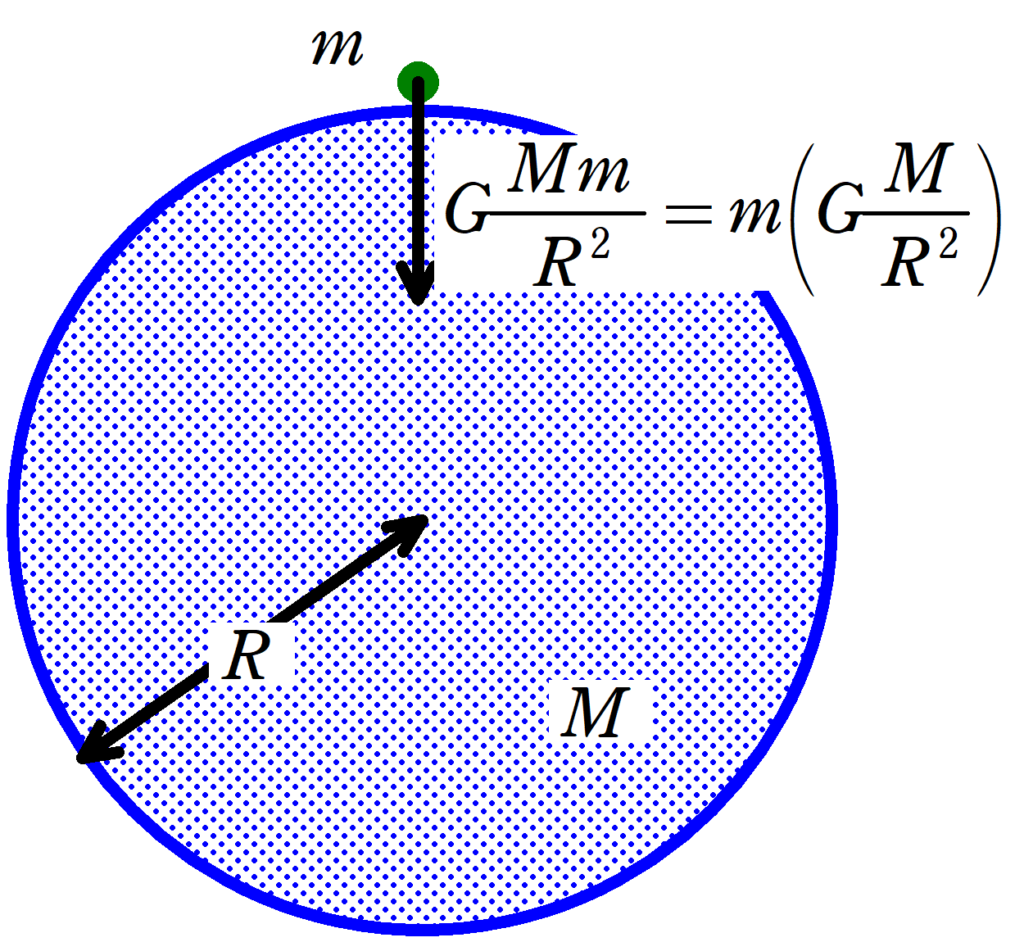
理由：上図より，$G\dfrac{Mm}{R^{2}}=mg$から，$gR^{2}=GM$

$G\dfrac{Mm}{R^{2}}=mg$より

$g=G\dfrac{M}{R^{2}}$　(答)

(2)　

NEKO

向心方向の運動方程式を立てます．

向心力は万有引力となります．

表面での万有引力は$mg$です．

円運動の加速度

半径$r$，円運動の接線方向の速さを$v$，角速度を$\omega$とすると，向心加速度の大きさ$a$は

$a=\dfrac{v^{2}}{r}=r\omega^{2}$

向心加速度の向きは円運動の中心

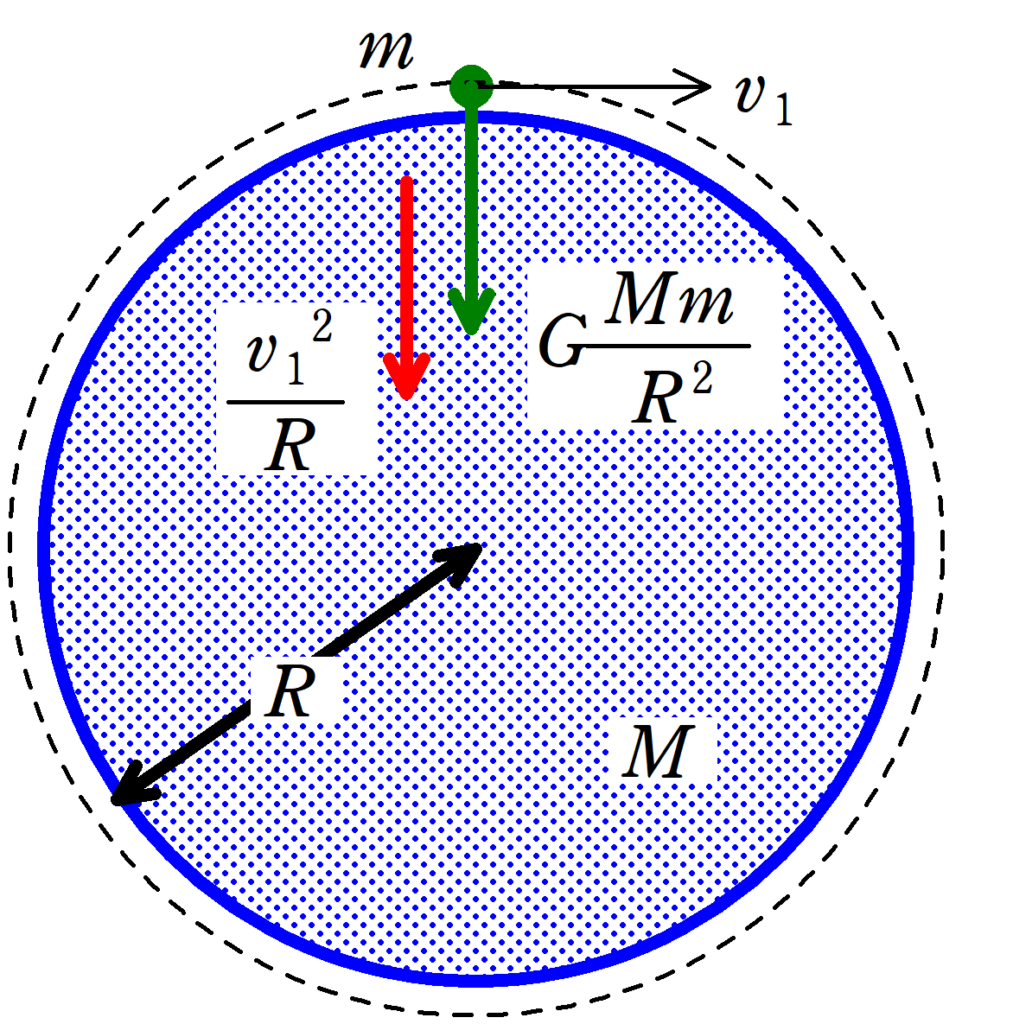
★　向心方向の運動方程式

万有引力は$G\dfrac{Mm}{R^{2}}$ですが，表面上では$mg$と同じです．

$m\dfrac{v_{1}^{2}}{R}=mg$

$\therefore　v_{1}=\sqrt{gR}$　$\dots　(\ast)$

PHYさん

このように惑星を1周するための速度$v_{1}$を第1宇宙速度といいます．

(3)　

NEKO

万有引力による位置エネルギーは次のようになります．

万有引力による位置エネルギー

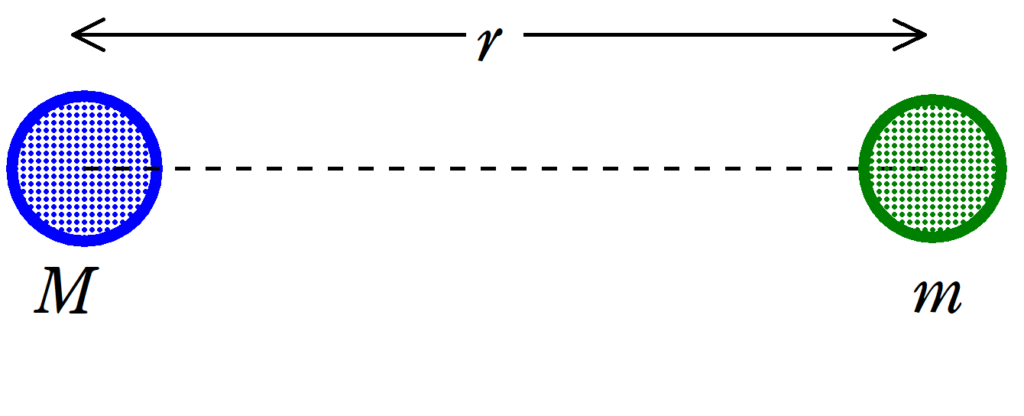
質量$M$と質量$m$の物体の距離を$r$とする．万有引力の位置エネルギーの基準点を無限遠とし，万有引力定数を$G$とすると，万有引力のよる位置エネルギー$U$は

$U=-G\dfrac{Mm}{r}$

NEKO

惑星Aで物体に速度を与えたときにギリギリ無限遠にいたくための条件は，無限遠で速度が0になることです．

無限遠で速度があるのであれば，惑星Aでもう少し速度の大きさを小さくしてもよいですからね．

力学的エネルギー保存則を立てて計算しましょう．

★　力学的エネルギー保存則

$\dfrac{1}{2}mv_{2}^{2}-G\dfrac{Mm}{R}=0+0$

(1)より，$gR^{2}=GM$であるから

$\dfrac{1}{2}mv_{2}^{2}-\dfrac{m}{R}\cdot gR^{2}=0+0$

$\therefore　v_{2}=\sqrt{2gR}$　(答)

PHYさん

このように無限遠にいくための最低速度を第2宇宙速度といいます．

次回の内容はこちらです．