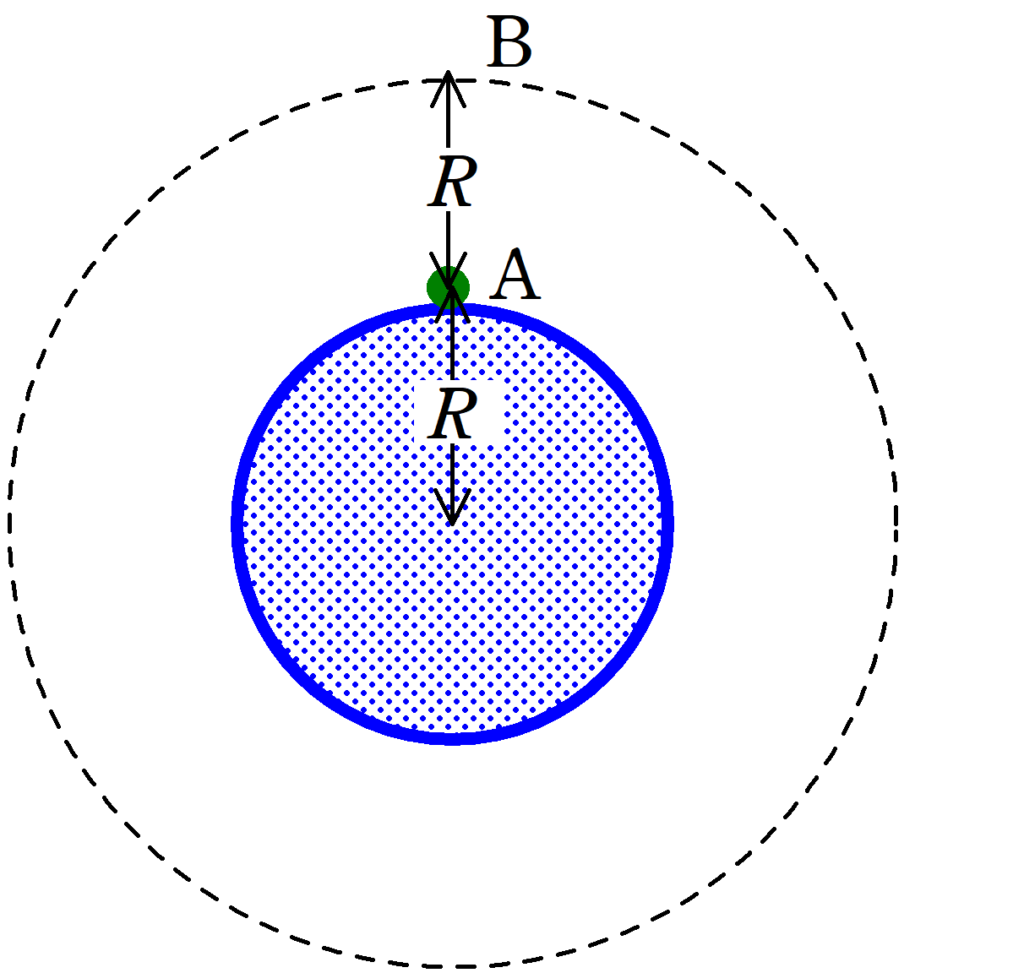
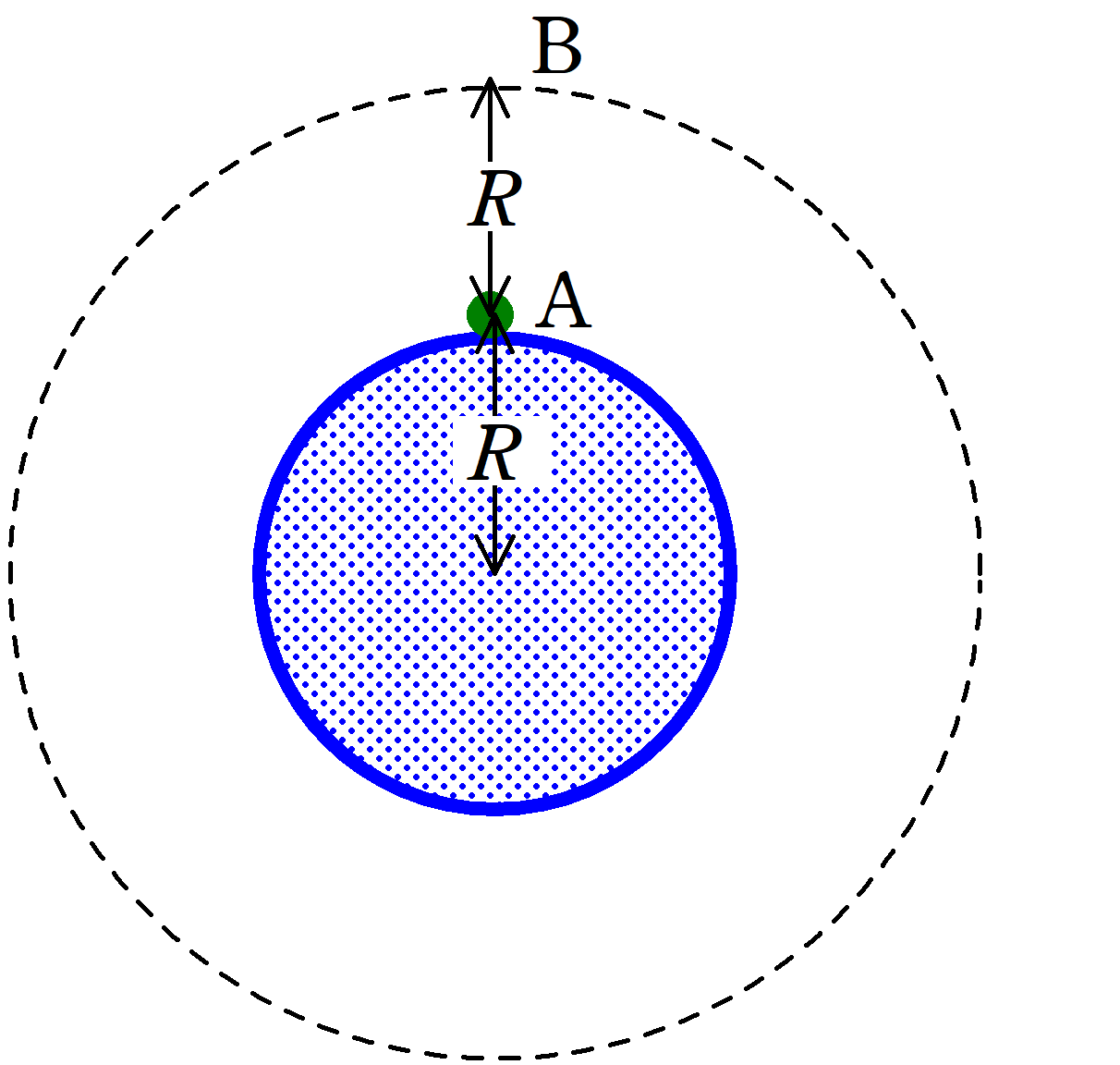
地球の質量を$M$,半径を$R$とする.地球の表面上のA点より,質量$m$の小さい物体に初速の大きさ$v_{0}$を鉛直上向きに与えたことろ,A点より高さ$R$の点Bで静止した.A点の重力加速度の大きさを$g$とし,地球の自転の影響,空気抵抗は無視する.
(1) $v_{0}$を$g$,$R$を用いて表せ.
(2) 点Bより小さいな物体を2つに分裂させたところ,片方が半径$2R$で中心が地球の中心と一致する等速円運動をした.このとき,円運動の速さ$v$を$g$,$R$を用いて表せ.
(3) (2)において,円運動の回転数$\nu$を$g$,$R$を用いてあらわせ.
<解答>

(1)の誤答例から紹介します.
※ 誤答例
力学的エネルギー保存則より
$\dfrac{1}{2}mv_{0}^{2}=mgR$
$v_{0}=\sqrt{2gR}$

何が間違っているの?

重力による位置エネルギーを使っているところが間違っています.
地球の半径ほどのスケールになってくると,重力加速度は場所によって異なります.
場所によって変化する重力加速度を一定とみなして計算していることでずれが生じます.
なので,万有引力による位置エネルギーを使って計算しましょう.
ただし,万有引力定数$G$が与えられていないので,次の変換式を使います.
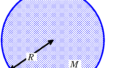
半径$R$で質量$M$の惑星の表面上の重力加速度の大きさを$g$とする.
惑星の自転の影響を無視するとき,重力加速度の大きさ$g$と万有引力定数$G$には次の関係がある.
$gR^{2}=GM$
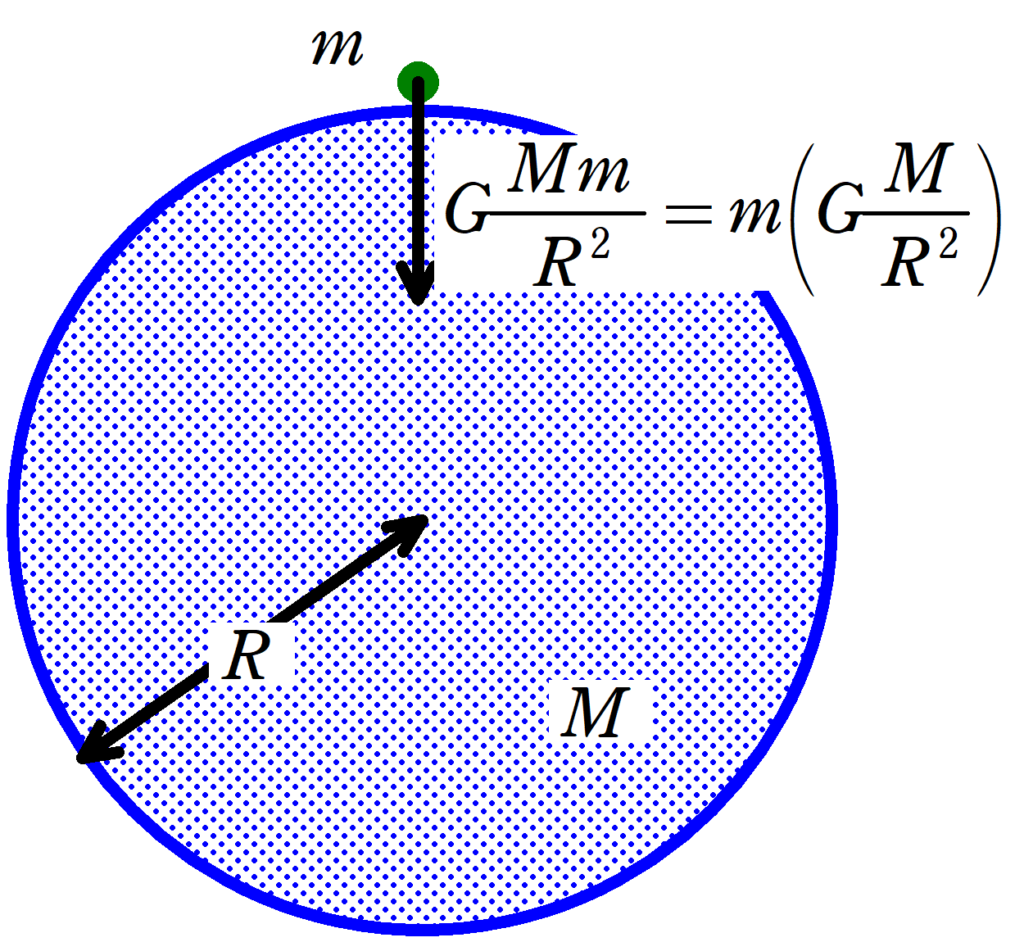
理由:上図より,$G\dfrac{Mm}{R^{2}}=mg$から,$gR^{2}=GM$

万有引力のよる位置エネルギーも確認しておきましょう.
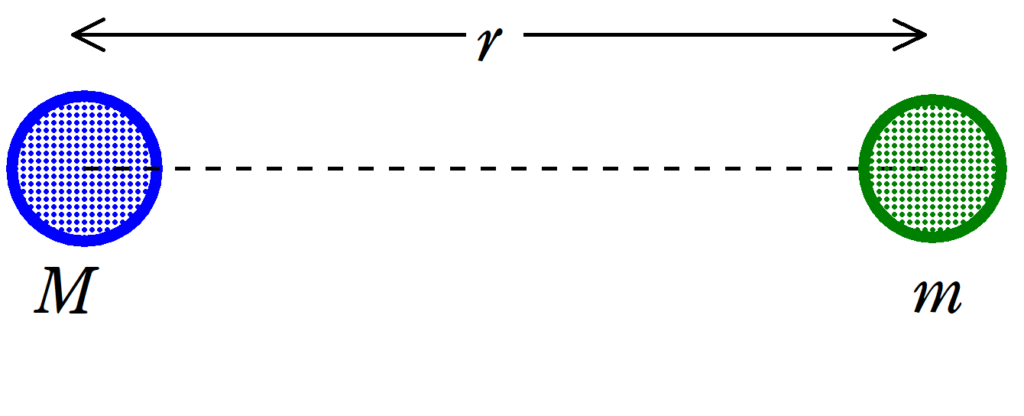
質量$M$と質量$m$の物体の距離を$r$とする.万有引力の位置エネルギーの基準点を無限遠とし,万有引力定数を$G$とすると,万有引力のよる位置エネルギー$U$は
$U=-G\dfrac{Mm}{r}$
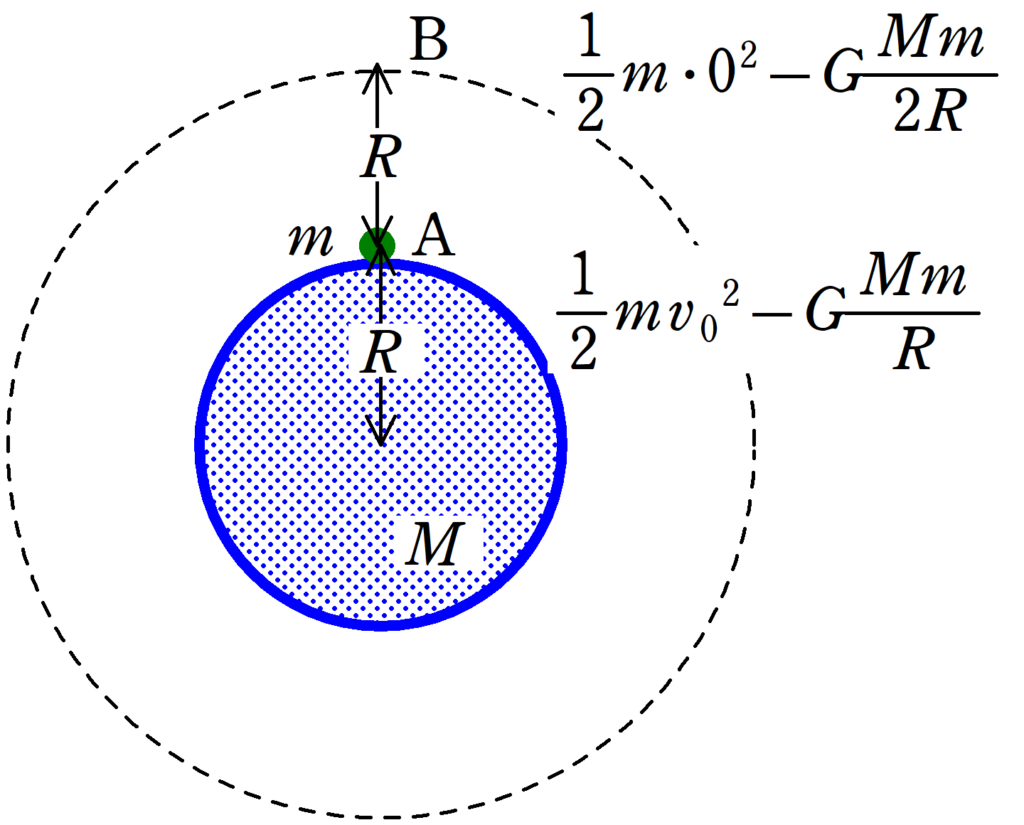
★ 力学的エネルギー保存則
$\dfrac{1}{2}mv_{0}^{2}-G\dfrac{Mm}{R}=0-G\dfrac{Mm}{2R}$
$v_{0}=\sqrt{\dfrac{GM}{R}}$
$GM=gR^{2}$を代入して
$v_{0}=\sqrt{\dfrac{gR^{2}}{R}}=\sqrt{gR}$ (答)
(2)

等速円運動の問題なので,次の2式を立てることを意識しましょう.
等速円運動の問題で立てて欲しい2式
- 向心方向の運動方程式
- 周期の式
★ 向心方向の運動方程式
速さを$v$として,運動方程式を立てる.
$m\dfrac{v^{2}}{2R}=G\dfrac{Mm}{(2R)^{2}}$
$v=\sqrt{\dfrac{GM}{2R}}$
$GM=gR^{2}$より
$v=\sqrt{\dfrac{gR^{2}}{2R}}=\sqrt{\dfrac{gR}{2}}$ (答)
(3)
等速円運動の半径を$r$,速さを$v$,角速度を$\omega$,回転数を$\nu$,周期を$T$とすると,以下の関係式が成り立つ.
$T=\dfrac{2\pi r}{v}=\dfrac{2\pi}{\omega}=\dfrac{1}{\nu}$

上式より,回転数$\nu$を求めます.
★ 回転数$\nu$
$\eqalign{T&=\dfrac{2\pi \cdot 2R}{v}\\&=4\pi R\sqrt{\dfrac{2}{gR}}\\&=4\pi\sqrt{\dfrac{2R}{g}}}$
したがって,
$\nu=\dfrac{1}{T}=\dfrac{1}{4\pi}\sqrt{\dfrac{g}{2R}}$ (答)

次回の内容はこちらです.

コメント
[…] […]