
今回は,体積が変化しない,いわゆる定積変化の問題です!
さっそく,問題をみてみましょう.
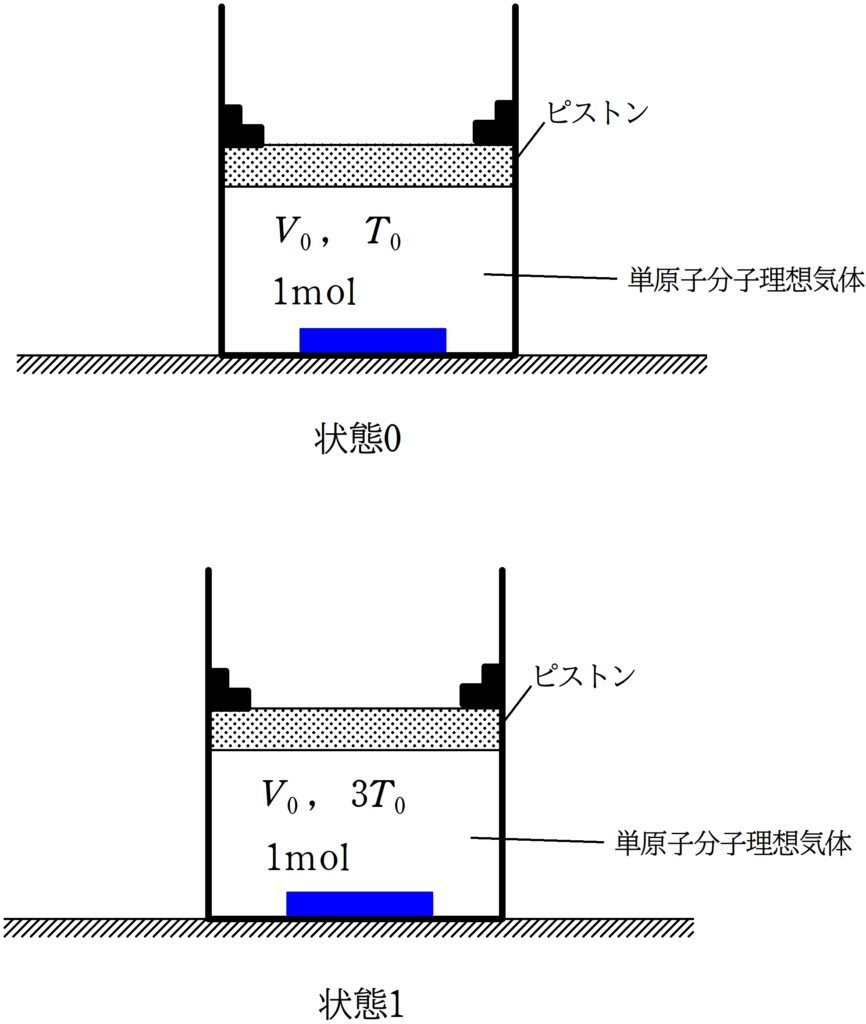
上図のように,水平な床の上に断熱容器が固定されている.
断熱容器の中には,熱を通さないピストンによって物質量$1 {\rm mol}$の単原子分子理想気体が封入されている.
はじめ,単原子分子理想気体の体積は$V_{0}$,絶対温度は$T_{0}$であった.この状態を状態0とする.
ピストンを固定したまま,温度調節器で気体をゆっくりとあたためると,絶対温度は$3T_{0}$となった.この状態を状態1とする.
気体定数を$R$として,次の問いに答えよ.
(1) 状態0のおける気体の圧力$p_{0}$を求めよ.
(2) 状態1における気体の圧力$p_{1}$を求めよ.
(3) 状態0から状態1までの間に気体がした仕事$W$と内部エネルギーの変化$\Delta U$と気体が吸収した熱量$Q$をそれぞれ求めよ.
<解答>
(1)

熱力学の問題では,基本的に次の3つの式を立てて欲しいのですが,今回に限っては
1.可動部分のつり合いの式
からは,いい情報が得られません.
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる
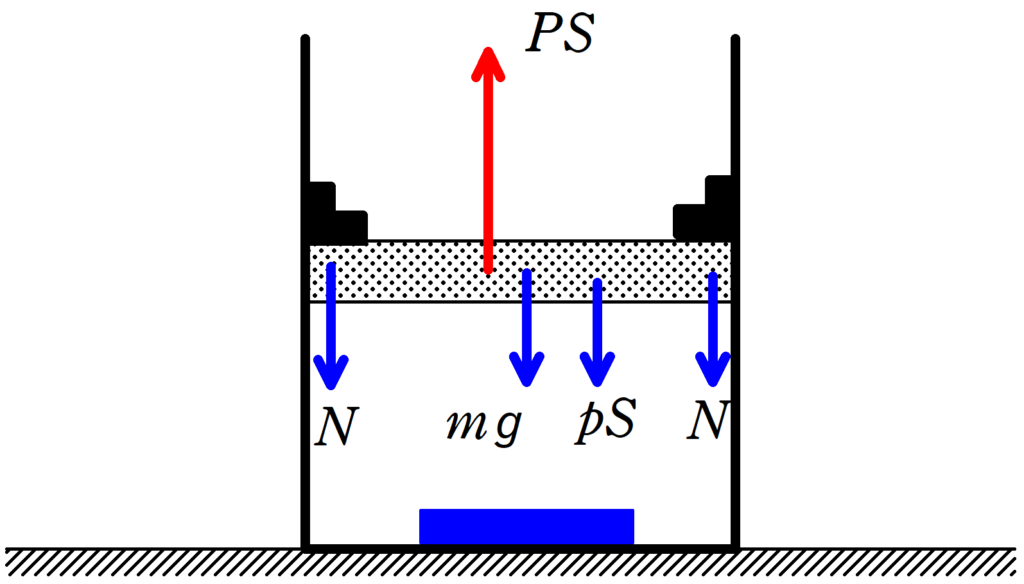

これは,ピストンにはたらく力である,固定されているときにはたらいている力が未知だからです.
定積変化のときは,可動部分のつり合いの式を考えてもうまくいかないことが多いでしょう.
なので
2.状態方程式
を立てて,計算をします.
理想気体では,気体の圧力を$p$,体積を$V$,物質量を$n {\rm mol}$,絶対温度を$T$,気体定数を$R$とすると,次の関係式が成り立つ.
$pV=nRT$
★ 状態0における理想気体の状態方程式
$p_{0}V_{0}=1\cdot RT_{0}$
$\therefore$ $p_{0}=\dfrac{RT_{0}}{V_{0}}$
(2)

次に,状態変化後の体積と絶対温度がわかっているので,ボイル・シャルルの法則を立てます.
理想気体について,物質量$n$が変化しないとき,気体の圧力を$p$,気体の体積を$V$,絶対温度を$T$とすると,
$\dfrac{pV}{T}=$一定
が成り立つ.(ボイル・シャルルの法則)
特に,温度が一定のとき
$pV=$一定(ボイルの法則)
圧力が一定のとき
$\dfrac{V}{T}=$一定(シャルルの法則)
が成り立つ.

今回は,体積が一定だから
$\dfrac{p}{T}=$一定
が成り立つね.
★ ボイル・シャルルの法則
$\dfrac{p_{1}}{3T_{0}}=\dfrac{p_{0}}{V_{0}}$
$\therefore$ $p_{1}=3p_{0}=\dfrac{3RT_{0}}{V_{0}}$
(3)

まず,気体がした仕事は0だね.
気体はピストンに力を加えているけど,ピストンを動かしていないわけだから
仕事=力×距離
の距離が0なんだね.
そして,内部エネルギーの変化$\Delta U$は次の式で求めよう!
,
問題分に単原子分子理想気体とかいてあるときは,次のことを使うことができる.
定積モル比熱が$\dfrac{3}{2}R$である.すなわち
内部エネルギー$U$は
$U=\dfrac{3}{2}nRT=\dfrac{3}{2}pV$
内部エネルギーの変化$\Delta U$は
$\Delta U=\dfrac{3}{2}nR\Delta T=\dfrac{3}{2}(p_{2}V_{2}-p_{1}V{1})$
※$n$:物質量,$T$:絶対温度,$p$:圧力,$V$:体積
★ 内部エネルギーの式
$\Delta U=\dfrac{3}{2}\cdot 1\cdot R(3T_{0}-T_{0})=3RT_{0}$

そして,熱量は熱力学第一法則で求めましょう.
内部エネルギーの変化を$\Delta U$,気体が吸収する熱量を$Q$,気体がした仕事を$W$とすると
$Q=\Delta U+W$
★ 熱力学第一法則
$Q=\Delta U+W=3RT_{0}$
以上より,答えは,$W=0$,$\Delta U=3RT_{0}$,$Q=3RT_{0}$


コメント
[…] […]