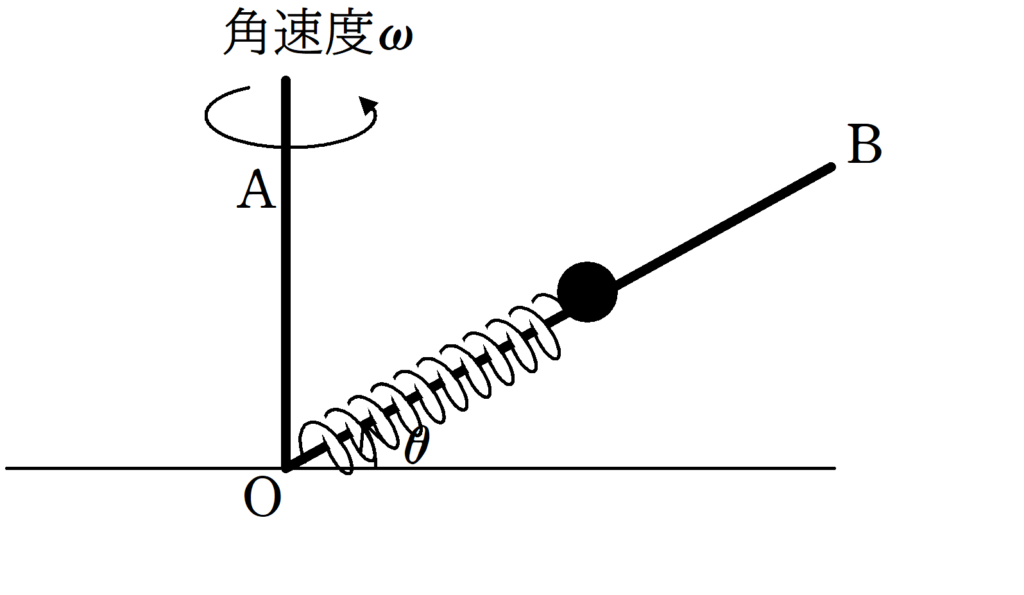
上図のように,水平な床の上に棒Aが床に対して垂直に固定されている.
さらに,Aと床の接触部分Oにて棒Bを床から$\theta$のなす角方向のとりつけ固定した.
ばね定数$k$の軽いばねを棒Bに通し,ばねの一端をOに固定し,他端に穴のあいた質量$m$の物体をとりつける.
ばねの自然長を$L_{0}$とする.ばねが自然長になるように物体を固定し,棒Aを角速度$\omega$でOを軸に回転させると,それにともない棒Bと物体もOAを軸に角速度$\omega$で回転した.
角速度を一定に保ったまま,固定をはずす.物体とともに軸OAまわりに回転する観測者からみると,物体は単振動をはじめた.
このとき,次の問いに答えよ.ただし,重力加速度の大きさを$g$とし,物体は摩擦力がはたらくことなくなめらかに運動できる.また,棒Bは十分長く,物体は棒Bの外に出ないようになっており,$\dfrac{L_{0}}{2}<\dfrac{kL_{0}-mg\sin\theta}{k-mw^{2}\cos^{2}\theta}$である.
(1) 固定をはずした後に,物体が単振動をするとき,,$m$,$k$,$\omega$,$\theta$の間に成り立つ関係式を求めよ.
(2) 単振動の周期を求めよ.
<解答>
(1)

今回も運動を方程式を立てることで,情報を読み取りましょう.
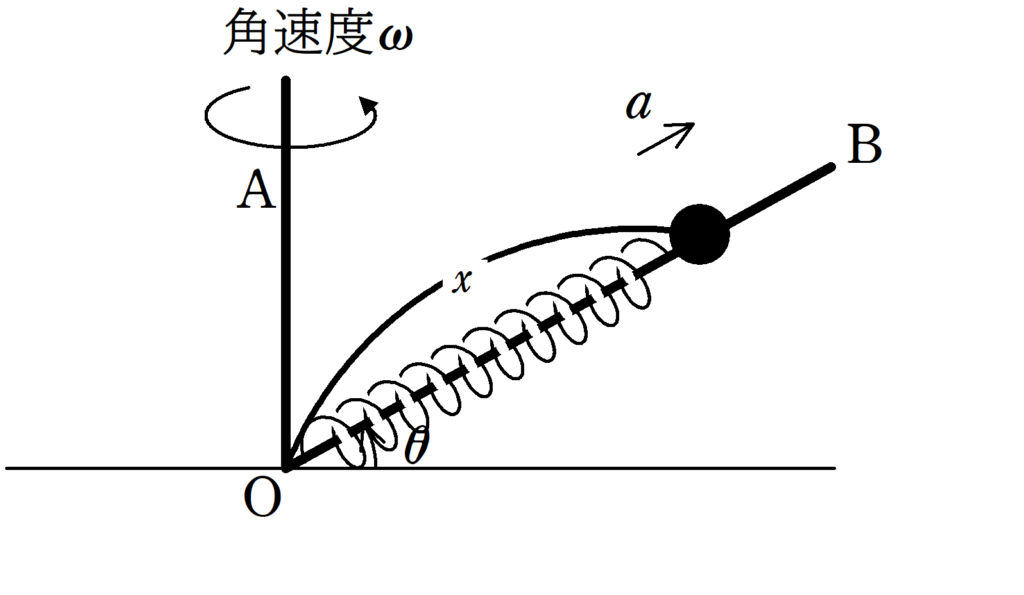

Oを原点として,OB方向に軸を$x$軸にとります.
ただし,OBはOAのまわりを角速度$\omega$で回転しています.
そのため,遠心力がはたらくことに注意しましょう.
遠心力は,次のようになります.
物体の質量が$m$,物体が軸のまわりに半径$r$,速さ$v$,角速度$\omega$で回転しているとき,物体とともに回転した観測者からみたときに,遠心力がはたらく.
遠心力の大きさを$f$とすると
$f=mr\omega^{2}=m\dfrac{v^{2}}{r}$
向きは回転軸に向かう方向と逆向き
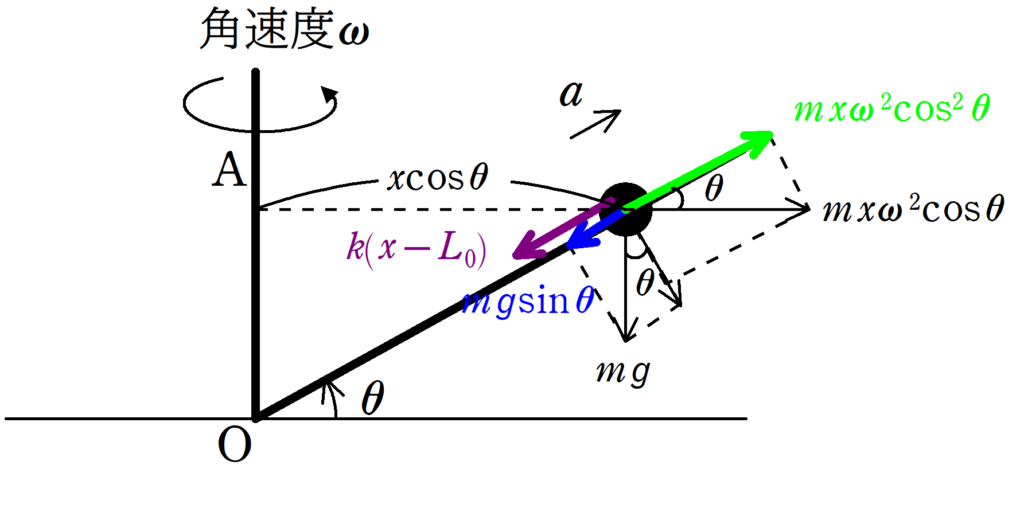

物体がOから距離$x$だけ離れているときに,物体とともに回転している観測者からみたときにはたらく力は
重力,弾性力,遠心力,棒Bとの間の抗力
があります.これらの力を棒Bの方向に分解し,運動方程式を立てましょう.
棒Bとの間の抗力は棒B方向に垂直なので,考えなくてもよいです.
さらに,重力の棒Bの方向の力は$mg\sin\theta$,弾性力は伸びているときを考えて,Oの方向に$k(x-L_{0})$,遠心力は$mx\omega^{2}\cos^{2}\theta$です.
物体の円運動の半径は$x$ではなく,$x\cos\theta$であることに注意してください.
OからBの方向を正にとり,加速度を$a$としましょう.
★ 運動方程式
$\eqalign{ma&=-k(x-L_{0})+(m\omega^{2}\cos^{2}\theta)x-mg\sin\theta\\&=-kx+kL_{0}+(m\omega^{2}\cos^{2}\theta)x-mg\sin\theta\\&=-(k-m\omega^{2}\cos^{2}\theta)x+kL_{0}-mg\sin\theta \dots (\clubsuit)}$

一見,どんな場合でも運動方程式になりそうな気がするのですが,実は
$ma=-k(x-x_{0})$
の$k$は正の比例定数ではないといけません.もし$k$が負であれば,加速度は$x$が大きくなればなるほど,$a$が大きくなるので,無限遠方にいってしまいます.
そこで,$(\clubsuit)$の式の$x$の係数部分の「-」を除いた$k-m\omega^{2}\cos^{2}\theta$が正であれば単振動するというわけです.
★ 単振動する条件
$k-m\omega^{2}\cos^{2}\theta>0$ (答)
(2)
質量を$m$,加速度を$a$,物体の座標を$x$,$x_{0}$を定数,$k$を正の定数とする.
運動方程式が以下で表されている.
$ma=-k(x-x_{0})$
このとき,振動の中心は$x_{0}$,角振動数$\omega$と周期$T$は次のようになる.
$\omega=\sqrt{\dfrac{k}{m}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$

$(\clubsuit)$を変形すると次のようになります.
$\eqalign{ma&=-(k-m\omega^{2}\cos^{2}\theta)x+kL_{0}-mg\sin\theta\\&=-(k-m\omega^{2}\cos^{2}\theta)(x-\dfrac{kL_{0}-mg\sin\theta}{k-m\omega^{2}\cos^{2}\theta})}$

この運動方程式の形から,振動の中心$x_{0}$は
$x_{0}=\dfrac{kL_{0}-mg\sin\theta}{k-m\omega^{2}\cos^{2}\theta}$
振動の周期$T$は
$T=2\pi\sqrt{\dfrac{m}{k-m\omega^{2}\cos^{2}\theta}}$ (答)


コメント