
誘電体の挿入によって,電気容量を求める問題はいくらかあります.
その際,「誘電率」が与えられるか,「比誘電率」が与えられるかをよく注意して問題を解いてください.
誘電率と比誘電率についてのまとめを確認したら,さっそく問題を解いてみましょう.
問題は2種類あります.
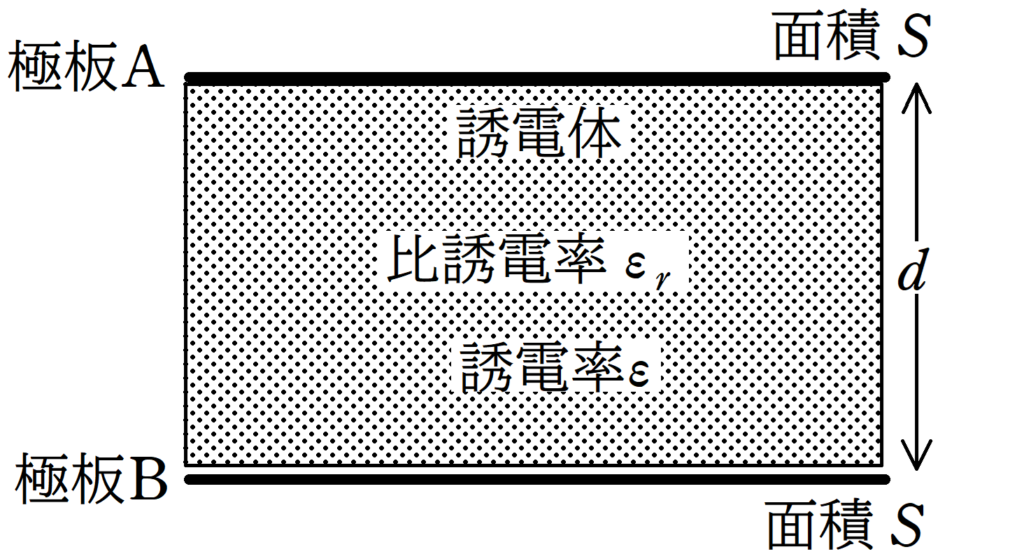
極板面積$S$の平板A,Bを距離$d$だけ隔てて固定しておく.
真空の誘電率を$\varepsilon_{0}$とすると,極板A,Bに何も入っていない場合の電気容量$C_{0}$は次のようになる.
$C_{0}=\varepsilon_{0}\dfrac{S}{d}$
このコンデンサーに比誘電率$\varepsilon_{\rm r}$,誘電率$\varepsilon$の誘電体で満たすとき,電気容量$C$は次のようになる.
$\eqalign{C&=\varepsilon\dfrac{S}{d}\\&=\varepsilon_{\rm r}\varepsilon_{0}\dfrac{S}{d}\\&=\varepsilon_{\rm r}C_{0}}$
また,$\varepsilon_{0}$,$\varepsilon$,$\varepsilon_{\rm r}$は次の関係がある.
$\varepsilon_{\rm r}=\dfrac{\varepsilon}{\varepsilon_{0}}$
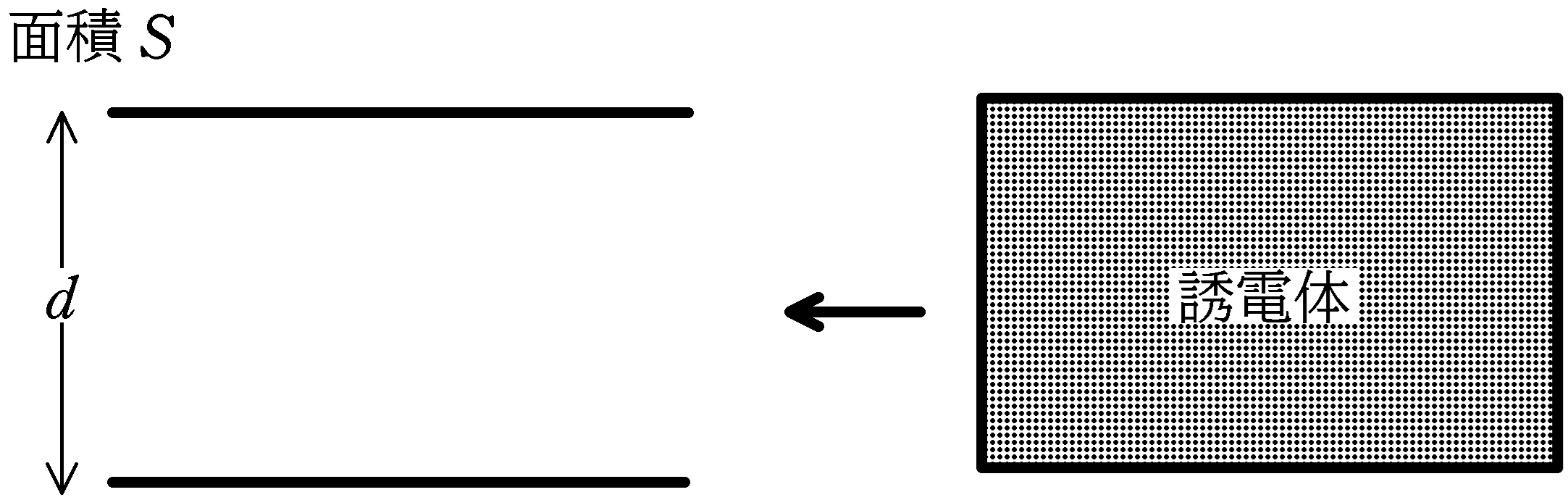
図のように,極板の距離$d$,面積$S$のコンデンサーを同形の誘電体で満たした.真空の誘電率$\varepsilon_{0}$として,次の問いに答えよ.
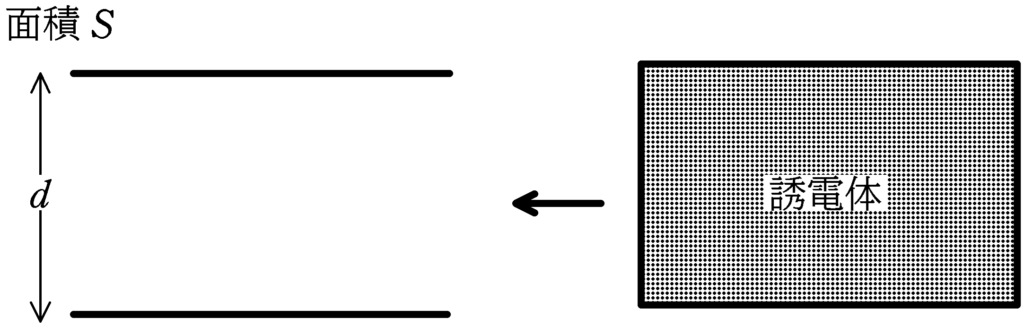
(1) 誘電体の誘電率が$\varepsilon$のとき,電気容量$C$を求めよ.
(2) 誘電体の比誘電率が$\varepsilon_{r}$のとき,電気容量$C$を求めよ.
<解答>
(1) コンデンサーの電気容量の式より
$C= \varepsilon \dfrac{S}{d}$ (答)
(2) コンデンサーの電気容量の式より
$C= \varepsilon_{r}\varepsilon_{0} \dfrac{S}{d}$ (答)

(1)は$\varepsilon_{0}$が$ \varepsilon$に変わったと考えるといいね.
あと,(2)は
$C= \varepsilon_{r}\times \varepsilon_{0} \dfrac{S}{d}$
と元のコンデンサーの$\varepsilon_{r}$倍になったと考えるといいね.
図のように,電気容量$C_{0}$のコンデンサーを同形の誘電体で満たした.このとき次の問いに答えよ.
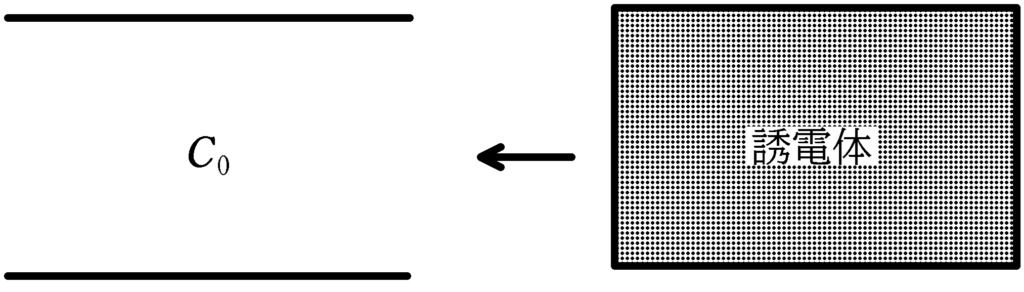
(1) 真空の誘電率を$\varepsilon_{0}$ とし,誘電体の誘電率が$\varepsilon$のとき,電気容量$C$を求めよ.
(2) 誘電体の比誘電率が$\varepsilon_{r}$のとき,電気容量$C$を求めよ.
<解答>
(1) 真空の誘電率を$\varepsilon_{0}$,極板面積を$S$,極板間距離を$d$とすると
$C_{0}= \varepsilon_{0} \dfrac{S}{d}$
より
$ \dfrac{S}{d}=\dfrac{C_{0}}{ \varepsilon_{0} }$
そこで,コンデンサーの電気容量の式より
$\eqalign{C&=\varepsilon\dfrac{S}{d}&= \varepsilon \cdot \dfrac{C_{0}}{ \varepsilon_{0} } }$ (答)
(2) 比誘電率$ \varepsilon _{r}$の誘電体で満たすので,電気容量は$\varepsilon_{0}$倍されるから
$C= \varepsilon_{r}C_{0} $ (答)

誘電率か,比誘電率のかはよく注意して読まないとね.
そもそも,比誘電率は無次元で,誘電率は$[\rm F/m]$であることも考えるといいよ.


コメント