ヤングの実験演習問題①

問題

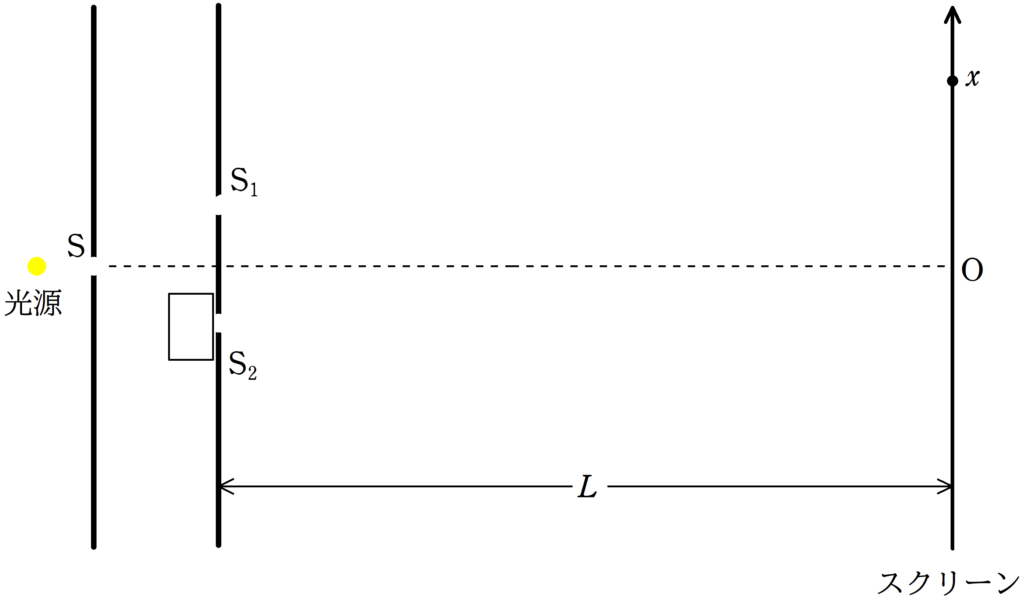
上図のように単スリット$\rm S$，2スリット$\rm S_{1} , S_{2}$のついたて，スクリーンが平行に設置されている．

スリット$\rm S_{1} , S_{2}$の距離が$d$，スリット$\rm S_{1} , S_{2}$のついたてとスクリーンまでの距離が$L$である．

スリット$\rm S$に空気中での波長$\lambda$の単色光を当てたところ，単色光は$\rm S_{1} , S_{2}$を通り，スクリーンに明暗の縞模様ができた．

(1)　明線との明線の間隔を求めよ．

次にスリット$\rm S_{2}$の前方（左側）に厚さが$D$，空気に対する相対屈折率$n(n>1)$の透明物質を図のようにおいた．このとき，次の問いに答えよ．

(2)　透明物質を入れる前と比べて，明線の位置はどの方向に，どれだけずれるか．

<解答>

(1)

PHYさん

まず，$\rm S_{1}$と$\rm S_{2}$の中点からスクリーンに下した垂線の足を原点$\rm O$として，スクリーン上の上方向を$x$軸の正方向にとります．

そして，座標$x$における明線条件を考えていきましょう．

NEKO

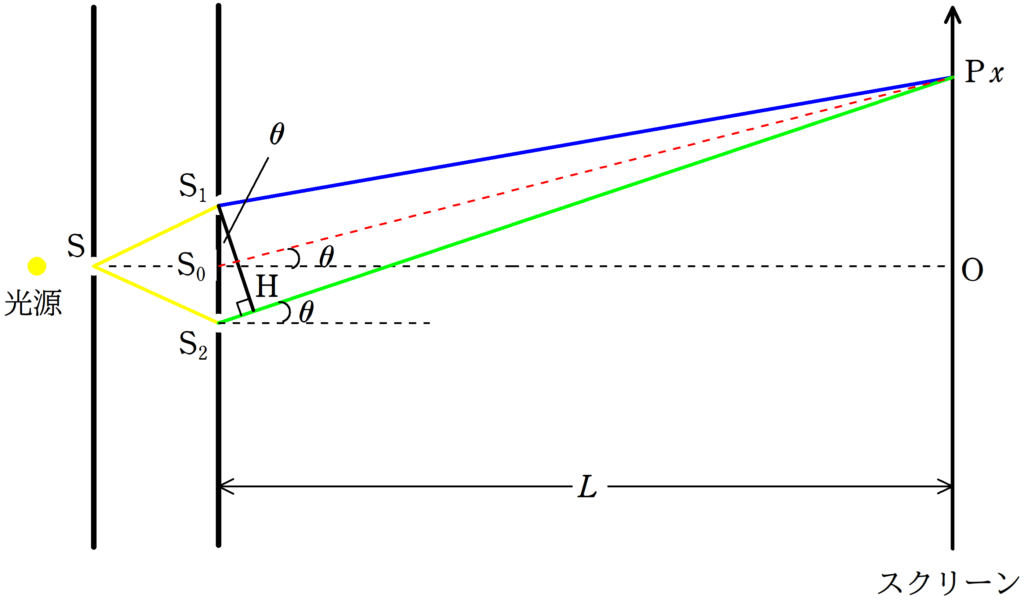
経路差の中にある波の数が整数個であれば，強め合うんだったよね．

NEKO

そして，経路差が

$d\sin\theta\approx \tan\theta \approx d\dfrac{x}{L}$

だから，強め合いの条件は，整数$m$を用いて

$\dfrac{d\dfrac{x}{L}}{\lambda}=m$　$\dots　(\ast)$

となるんだったね．

ここで，$|m|$は波の数に相当するんだったね．

$m$自体は次数と呼ばれているよ．

次数$m$の座標であることを強調して，$x$→$x_{m}$と表現してみましょう．

$(\ast)$について

$\eqalign{\dfrac{d\dfrac{x_{m}}{L}}{\lambda}&=m\cr d\dfrac{x_{m}}{L}&=m\lambda \cr x_{m}&=\dfrac{mL\lambda}{d}}$

PHYさん

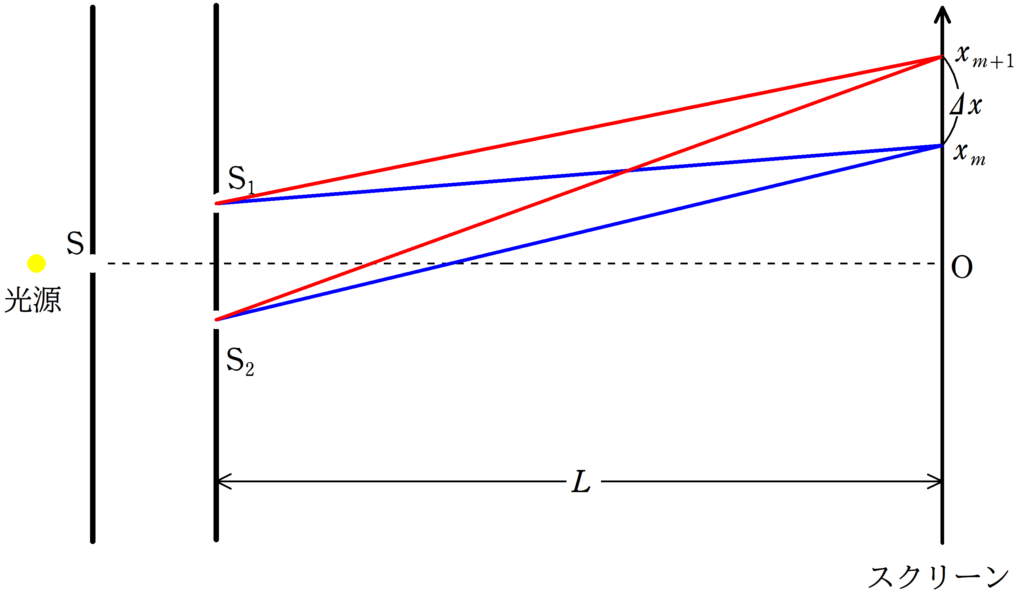
明線の間隔$\Delta x$は

$\Delta x=x_{m+1}-x_{m}$

ですね．

$\eqalign{\Delta x&=x_{m+1}-x_{m}\\&=\dfrac{(m+1)L\lambda}{d}-\dfrac{mL\lambda}{d}\\&=\dfrac{L\lambda}{d}}$

答えは$\Delta x=\dfrac{L\lambda}{d}$

(2)　

NEKO

透明物質を入れても経路が変化しないから，何も変わらないんじゃないの？

PHYさん

本質は経路差ではありません．

位相差です．

光が透明物質に入ることによって，波の数の差が生じます．

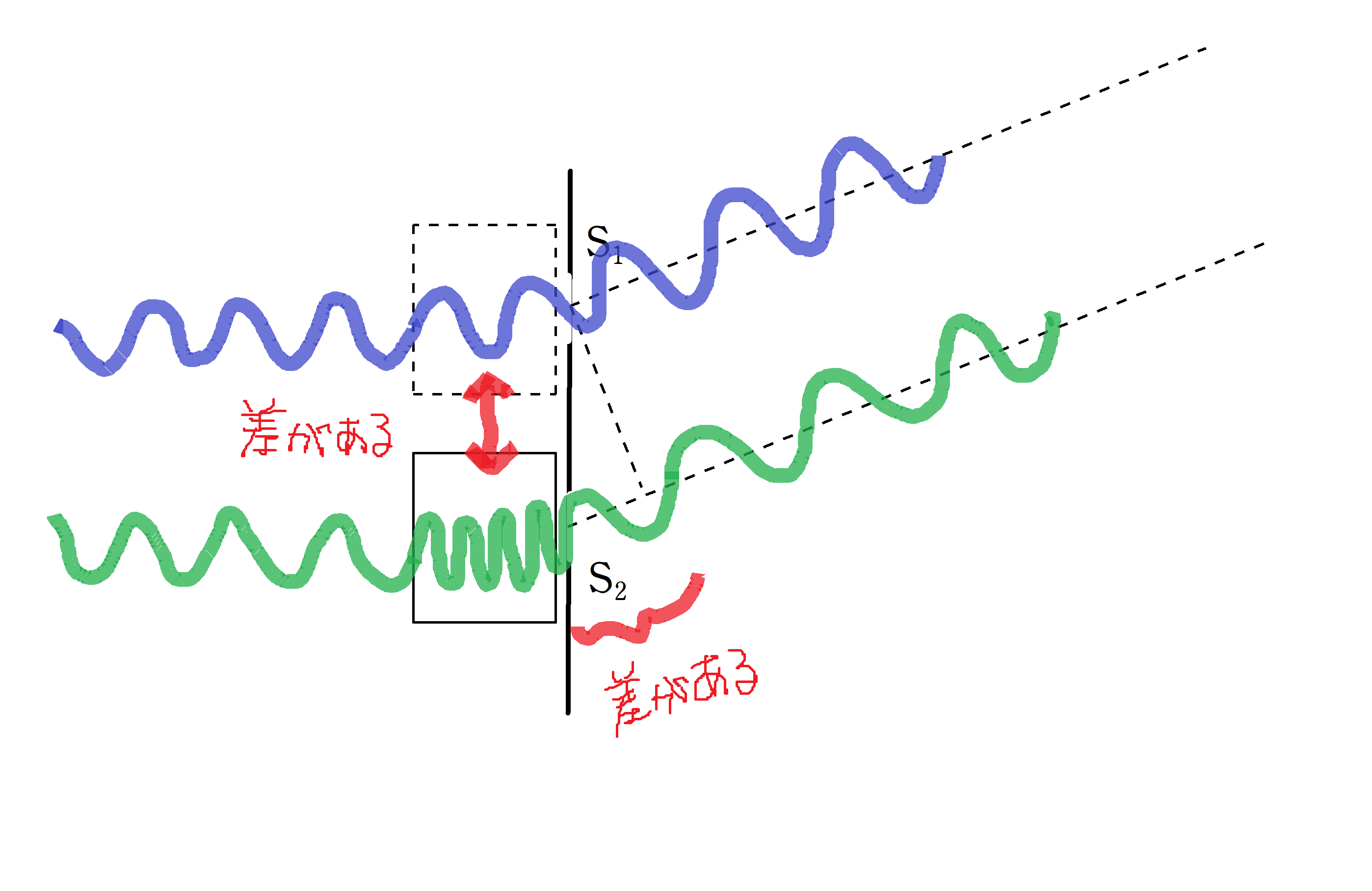
次の図をみてください．

PHYさん

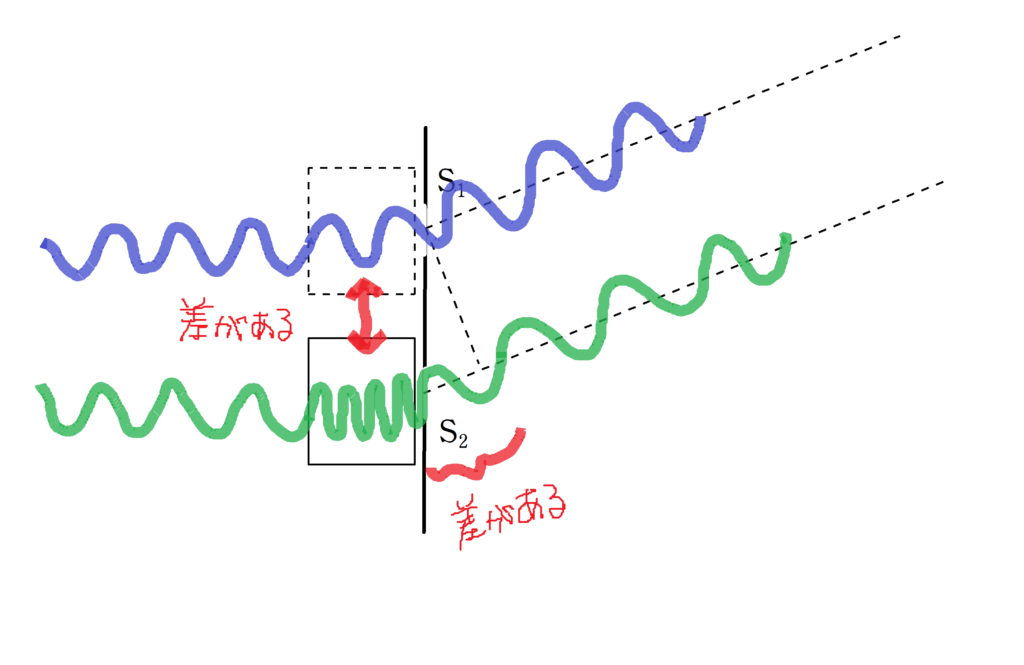
光が屈折率$n$の物質に入ると，波長は$\dfrac{1}{n}$倍になります．

そのため，透明物質がある分，波の数の差ができます．

NEKO

つまり，波の数の差で式を立てると，次のようになるんだね．

$\dfrac{d\dfrac{x_{m}^{\prime}}{L}}{\lambda}+\left(\dfrac{D}{\dfrac{\lambda}{n}}-\dfrac{D}{\lambda}\right)=m$

$\therefore　x_{m}^{\prime}=\dfrac{mL\lambda}{d}-\dfrac{(n-1)LD}{d}$

もともと，$x_{m}=\dfrac{mL\lambda}{d}$であったので，これを代入すると

$x_{m}^{\prime}=x_{m}-\dfrac{(n-1)LD}{d}$

NEKO

$n>1$だから，透明物質を入れると，$x$軸の負の向きに$\dfrac{(n-1)LD}{d}$ずれるんだね．