
波の干渉を考える場合,位相差が$0,\pm 2\pi,\pm 4\pi,\cdots$なら強め合いで位相差が$\pm \pi,\pm 3\pi,\pm 5\pi$なら弱め合いなんだよね.
じゃあ,それ以外の位相差のときはどうなるんだろう??
・「位相」についてよくわからない人は「位相ってなに?」
・「位相差による条件」がよくわからない人は「位相差のススメ」
を読んでいただくとよいかと思います.
また,
・「位相差の演習問題」がやりたい人は「干渉の演習問題」
を参考にしてください.

では,位相差が$\delta$である2つの波を合成してみましょう.
波1が振幅$a\,(>0)$,角振動数$\omega$で,時刻$t$における波の変位$y_{1}$を
$y_{1}=a\sin(\omega t)$
波2が振幅$a\,(>0)$,角振動数$\omega$で,時刻$t$における波の変位$y_{2}$を
$y_{2}=a\sin\left(\omega t+\delta\right)$
として,和から積の変換式で変換していきます.
合成波の変位$y$は
$\eqalign{y&=y_{1}+y_{2}\\&= a\sin(\omega t) + a\sin\left(\omega t+\delta\right) \cdots (\sharp)}$
まず,正弦の加法定理を書き出します.
$\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta$ $\cdots (\ast)$
$\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta$ $\cdots (2\ast)$
$(\ast)+(2\ast)$を計算します.
$\sin(\alpha+\beta)+\sin(\alpha-\beta)=2\sin\alpha\cos\beta$ $\cdots (\clubsuit)$
この式と$(\sharp)$との対応関係を書き出しましょう.
$\alpha+\beta= \omega t+\delta $ $\cdots (3\ast)$
$\alpha-\beta= \omega t $ $\cdots (4\ast)$
$(3\ast)+(4\ast)$を計算し,$\alpha$を求めます.
$2\alpha=2\omega t+\delta$
$\therefore \alpha=\omega t+\dfrac{\delta}{2}$ $\cdots (5\ast)$
$(3\ast)-(4\ast)$を計算し,$\beta$を求めます.
$2\beta=\delta$
$\therefore \beta=\dfrac{\delta}{2}$ $\cdots (6\ast)$
$(5\ast)$,$(6\ast)$を$(\clubsuit)$の右辺に代入して積の形をつくります.
$2\sin\left(\omega t+\dfrac{\delta}{2}\right)\cos\left(\dfrac{\delta}{2}\right)$
したがって,
振幅$=2a \cos\left(\dfrac{\delta}{2}\right) \sin\left(\omega t+\dfrac{\delta}{2}\right) $

$\sin$の部分は時間$t$が含まれていて,時間$t$によって変化します.
この波の振幅は$2a \cos\left(\dfrac{\delta}{2}\right) $の絶対値を取ったものとなります.
そこで,縦軸を振幅,横軸を位相差$\delta$とした,グラフをかいてみましょう.
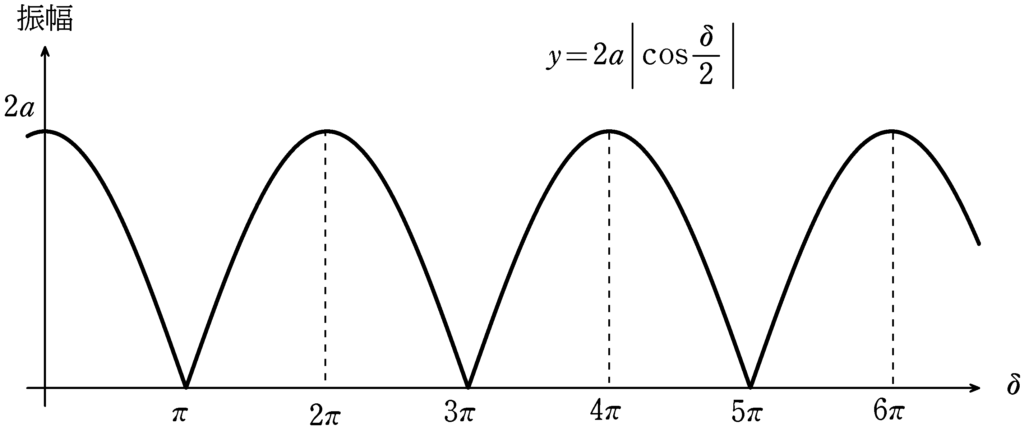

これを見ると,たとえば,位相差が$0$と$\pi$の間であれば,位相差$0$ほどではないけど,振幅はあるんだね.
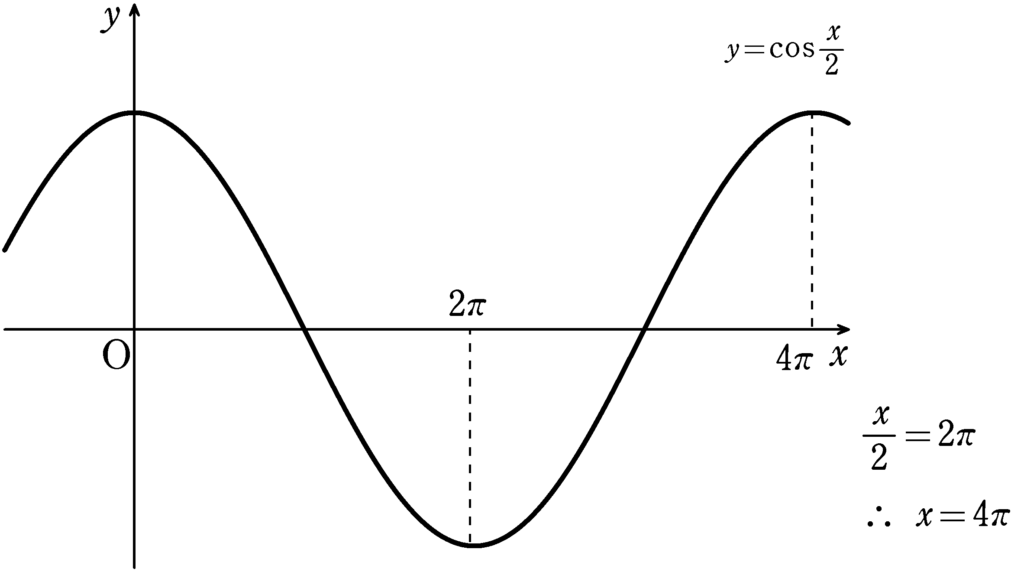
ちなみに,振幅$=|\cos(\delta/2 )|$のグラフは$y=\cos(x /2)$のグラフをかいて$y$が負の部分を折り返せばいいね.

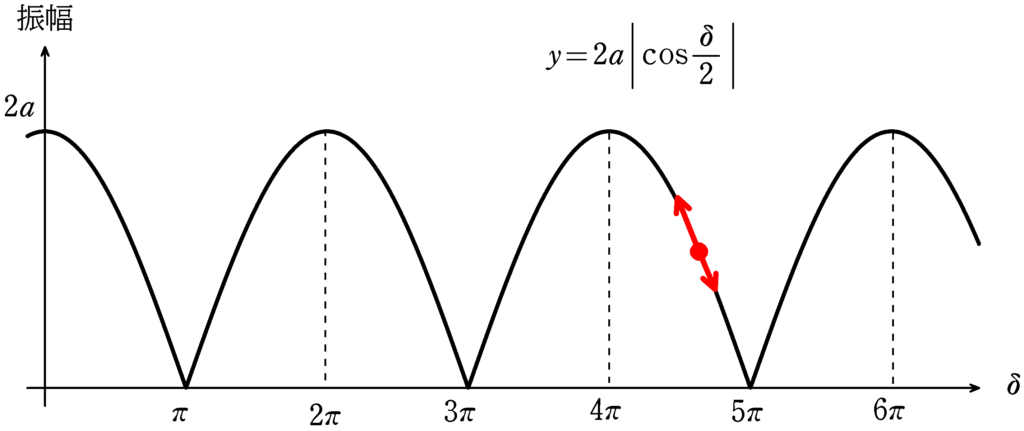
また,たとえば,位相差が$4\pi$と$5\pi$の中間あたりであるところから,何かのきっかけで位相差$4\pi$に近づくときはだんだんと振幅が大きくなります.
一方,何かのきっかけで$5\pi$に近づくときはだんだんと振幅が小さくなります.

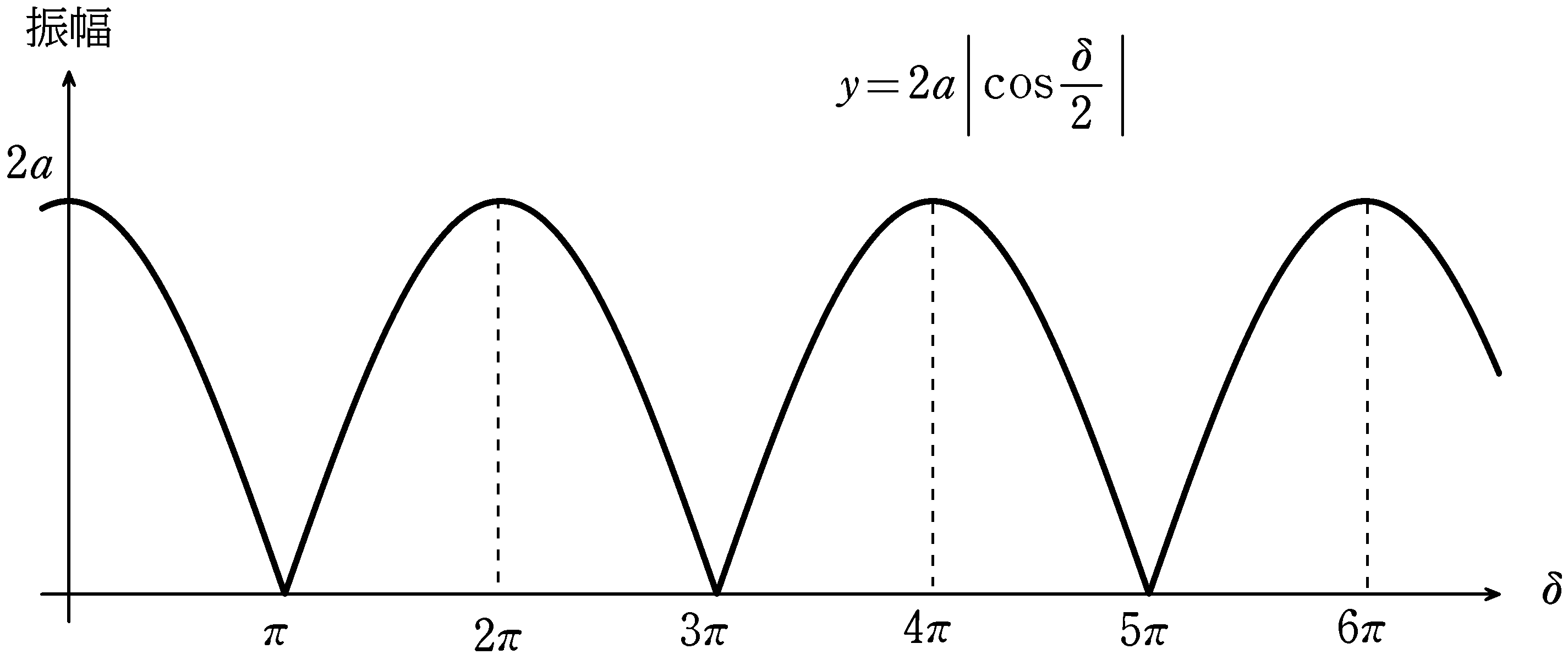
こういう話は「マイケルソン干渉計」でよく出てくるね.



コメント