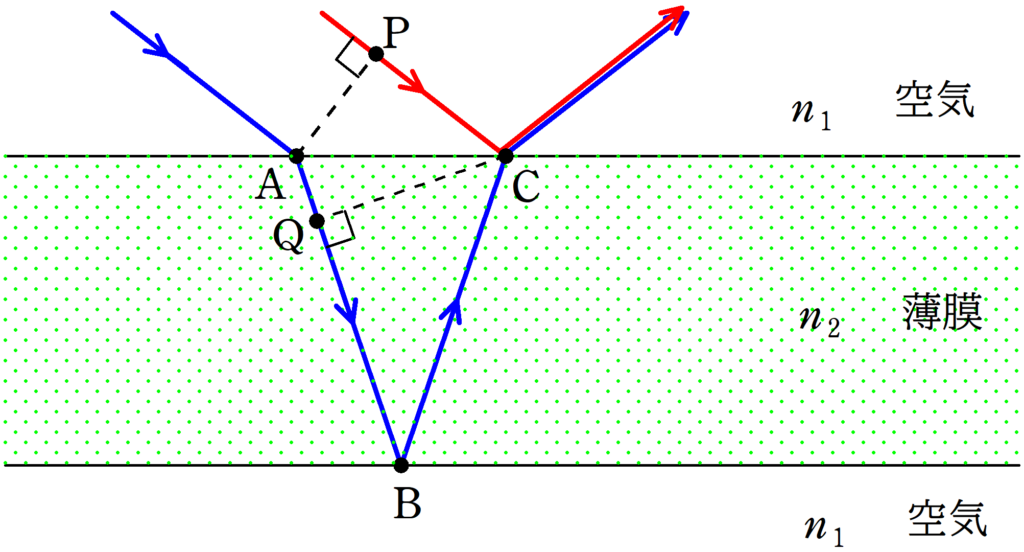
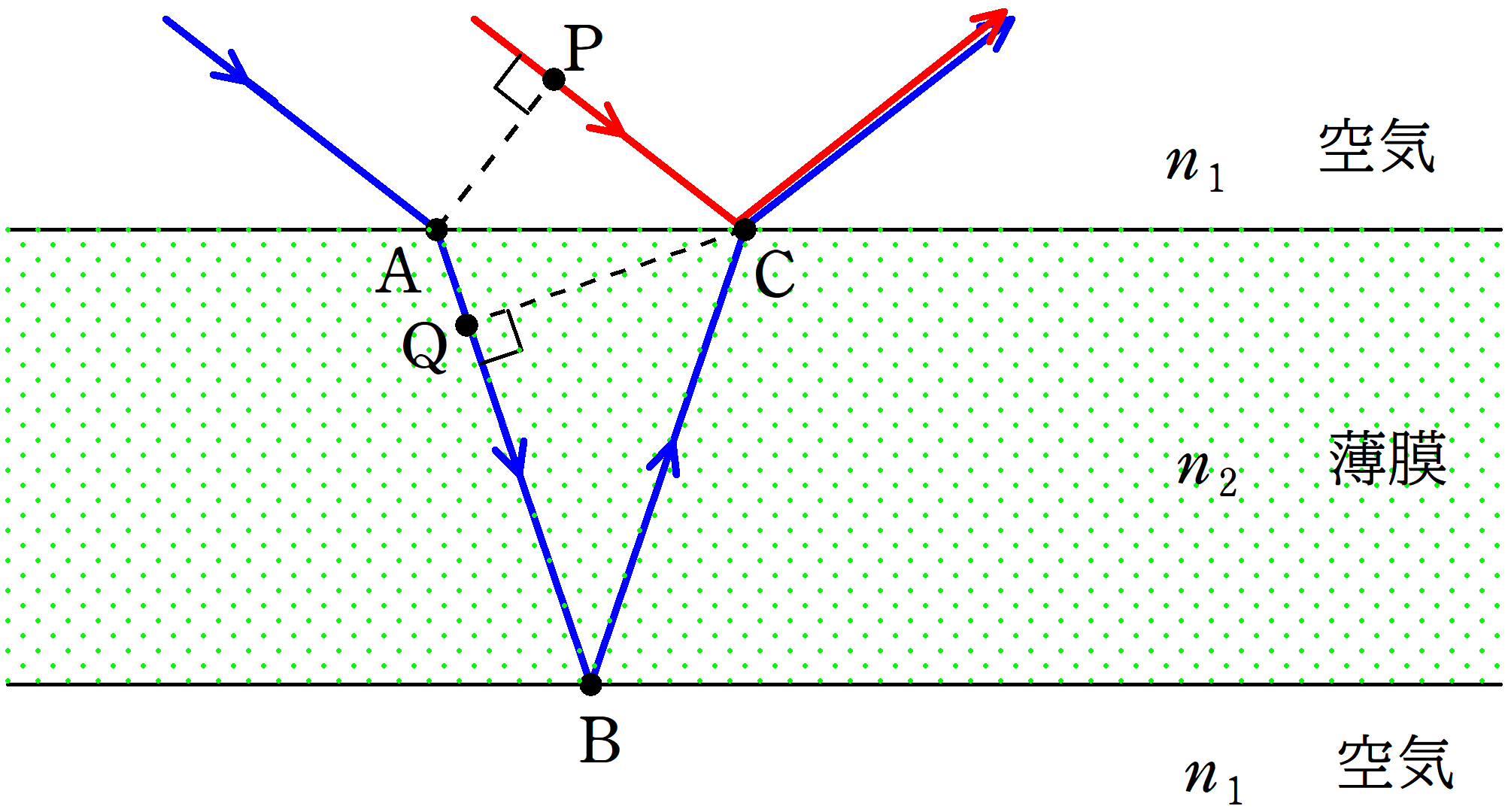
薄膜の干渉の問題で，よく上のような図が出てくるよね．
このとき，青い光の経路と赤い光の経路の差は
$\rm{ABC-PC}$
だと思っていたんだけど，なぜか問題集の解答では
$\rm{QBC}$
の部分を経路差として計算していたんだよ．
なんでこんな風になるんだろう？
正確には，
位相差が生じる経路の差
ですね．理由は
$\rm{PC}$部分と$\rm{AQ}$部分には位相差がない
からです．
それでは，$\rm{PC}$部分と$\rm{AQ}$部分には位相差がないことを確認しましょう．
まず，入射角と屈折角をそれぞれ$\theta_{1}$，$\theta_{2}$と設定します．
すると，$\rm{AQ}$部分の長さと$\rm{PC}$部分の長さはそれぞれ$\rm{AC}$，$\theta_{1}$，$\theta_{2}$を使ってどのように表すことができるでしょうか？
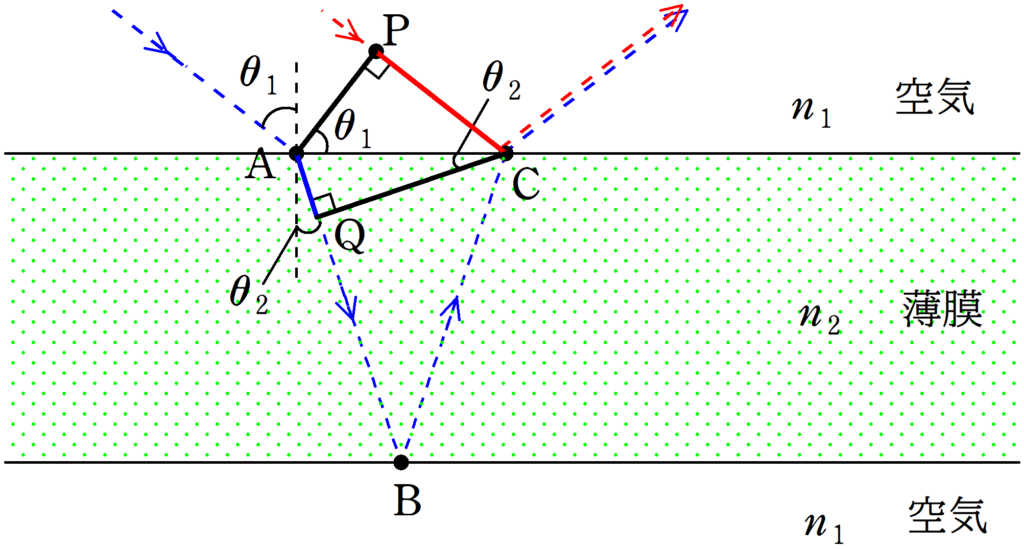
2つの直角三角形$\bigtriangleup \rm{AQC}$と$\bigtriangleup \rm{CPA}$の三角比を考えれば
$\rm{AQ}=\rm{AC}\sin \theta_{2}$，$\rm{PC}=\rm{AC}\sin \theta_{1}$
となるね．
次に入射角$\theta_{1}$，屈折角$\theta_{2}$，そして空気の波長$\lambda_{1}$と薄膜での波長$\lambda_{2}$の関係はどのようになりますか？
屈折の法則より
$\dfrac{\sin \theta_{1}}{\sin \theta_{2}}=\dfrac{\lambda_{1}}{\lambda_{2}}$
だね．
そうです．その式は次のようにも変形できますね．
$\dfrac{\lambda_{1}}{\sin\theta_{1}}=\dfrac{\lambda_{2}}{\sin\theta_{2}}$ $\dots (\ast)$
では，最後に位相差についてです．
経路に対応する位相は次のように比例式を立てるとよいでしょう．
★経路$\rm{PC}$部分による位相のずれ$\phi_{1}$
$2\pi : \lambda_{1} = \phi_{1} : \rm{PC}$
$\eqalign{\phi_{1}&=\dfrac{2\pi}{\lambda_{1}}\rm{PC}\\&=\dfrac{2\pi}{\lambda_{1}}\rm{AC}\sin \theta_{1}}$ $\dots (\clubsuit)$
★経路$\rm{AQ}$部分による位相のずれ$\phi_{2}$
$2\pi : \lambda_{2} = \phi_{2} : \rm{AQ}$
$\eqalign{\phi_{2}&=\dfrac{2\pi}{\lambda_{2}}\rm{AQ}\\&=\dfrac{2\pi}{\lambda_{2}}\rm{AC}\sin \theta_{2}}$ $\dots (\spadesuit)$
$(\ast)$の$\dfrac{\lambda_{1}}{\sin\theta_{1}}=\dfrac{\lambda_{2}}{\sin\theta_{2}}$を$(\clubsuit)$に代入すると$(\spadesuit)$になるね！
$\eqalign{\phi_{1}&=\dfrac{2\pi}{\lambda_{1}}\rm{AC}\sin \theta_{1}\\&=\dfrac{2\pi}{\lambda_{2}}\rm{AC}\sin \theta_{2}\\&=\phi_{2}}$
$\phi_{1}=\phi_{2}$だからこの部分の位相差は考えなくてもいいんだ．
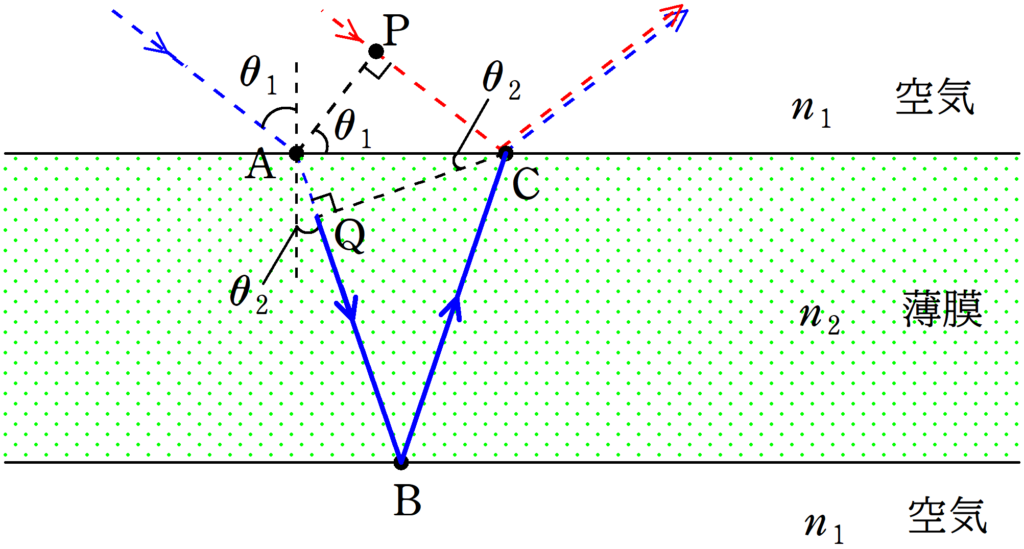
$\rm{PC}$部分と$\rm{AQ}$部分には位相差がないことを確かめたので，残りの$\rm{QBC}$部分の経路による位相差を調べましょう．
次のように少し工夫して計算するとよいです．
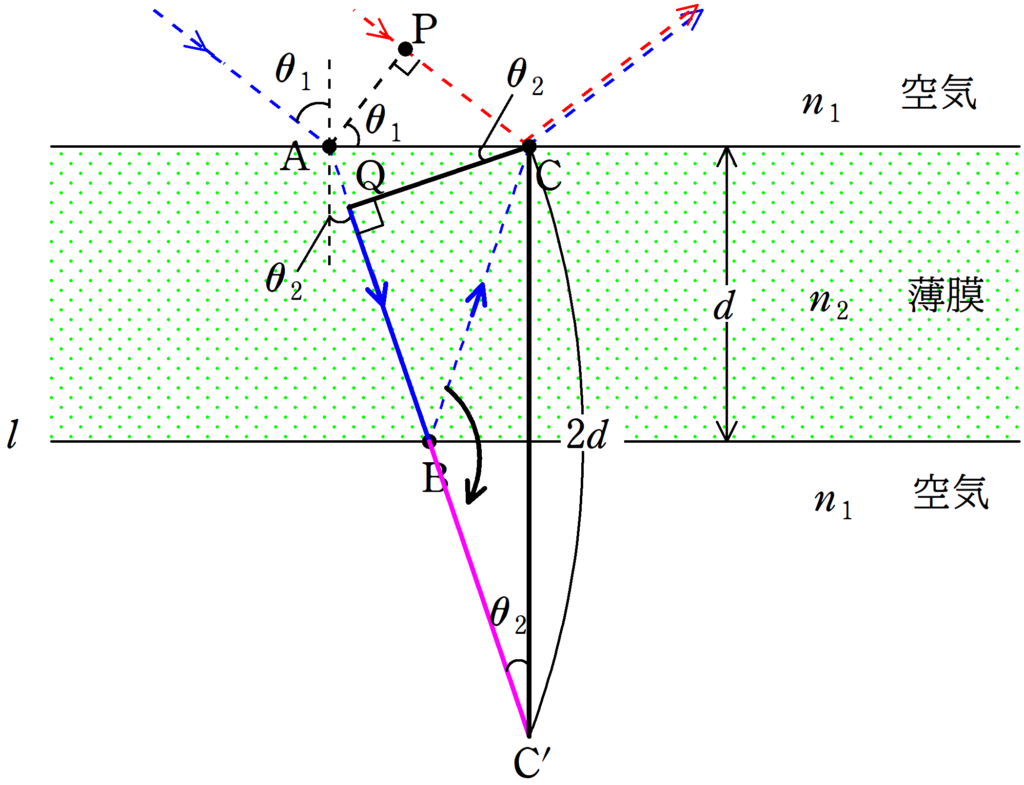
$\rm{BC}$部分を薄膜と空気の境界である直線$l$について折り返します．
すると，$\rm{QB+BC}$の代わりに$\rm{QB+BC’=QC’}$を計算すればいいことが確認できます．
そこで，直角三角形$\bigtriangleup {\rm CQC’}$を考えます．
${\rm CC’}=2d$であり，平行線の錯角から$\angle \rm{CC’Q}=\theta_{2}$なので，
${\rm QC’}=2d\cos \theta_{2}$
となります．
では，これを位相差に直そう！
位相差を$\phi$として，，，
$\eqalign{2\pi : \lambda_{2}&=\phi : 2d\cos\theta_{2}\cr \phi &=\dfrac{2\pi}{\lambda_{2}}\cdot 2d\cos\theta_{2}\cr \phi &=\dfrac{4\pi d \cos \theta_{2}}{\lambda_{2}}}$
確か，位相差が生じる原因は次の3つだったね．
位相差$\phi$は主に次の3つの位相差によって決まる．
$\phi_{1}$：初期位相のずれ
$\phi_{2}$：反射による位相のずれ
$\phi_{3}$：距離の差（屈折率が変わることで生じる光学的な距離の差を含む）による位相のずれ
このとき，位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$
はい．なので，反射による位相のずれも考えましょう．
$n_{2}>n_{1}$とします．
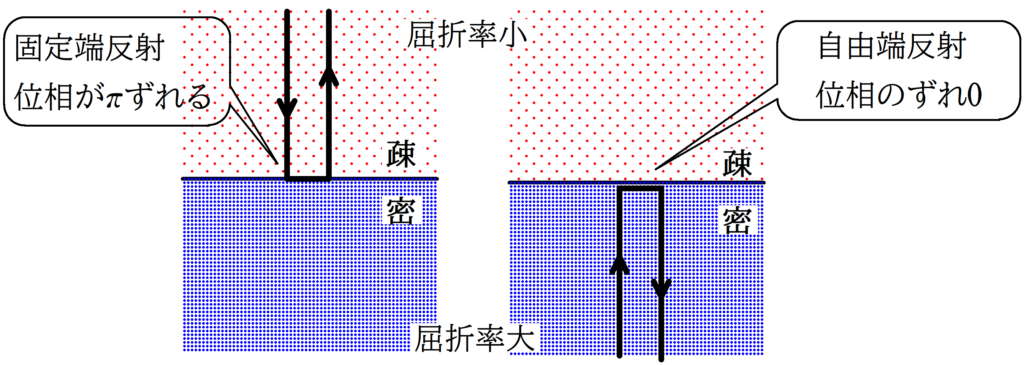
すると，赤の経路の反射であるCでは固定端反射し，青の経路であるBでは自由端反射します．
じゃあ，片方は位相が$\pi$ずれて，もう片方は位相のずれはないので，合計位相が$\pi$ずれるね．
念のため，自由端反射と固定端反射の位相のずれも次の図で確認しておこう．
そして，強め合いの条件と弱め合いの条件の確認です．
地点Pにおける2つの波の位相差を$\phi$，整数を$m$とすると，
強め合いの条件：$\phi=2\pi m$
弱め合いの条件：$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる．
$\phi_{1}$：初期位相のずれ
同位相なら$\phi_{1}=0$，逆位相なら$\phi_{1}=\pi$
$\phi_{2}$：反射による位相のずれ
自由端反射なら$\phi_{2}=0$，固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$：距離の差（屈折率が変わることで生じる光学的な距離の差を含む）による位相のずれ
距離の差が$\Delta l$のとき，次の比例式を立てて，位相差$\phi_{3}$を計算する．
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき，位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$
じゃあ，今回の強め合いの条件と弱め合いの条件は次のようになるね．
★強め合いの条件
$\dfrac{4\pi d \cos \theta_{2}}{\lambda_{2}} +\pi =2\pi m$
もし選択式の問題の場合は，上の形を変形したものがでる可能性もあります．
適する形に変形できるようにしておきましょう．
また，今回は反射による位相差が$\pi$としましたが，屈折率の関係によっては，ずれがないこともあるので，その都度考えて下さい．
★弱め合いの条件
$\dfrac{4\pi d \cos \theta_{2}}{\lambda_{2}} +\pi =(2m-1)\pi$
上図において，$\rm PC$と$\rm AQ$部分の位相差はないので，距離による位相差は$\rm QBC$の部分だけを考えればよい．
コメント
[…] [薄膜の干渉]位相差が生じる経路の長さ […]
[…] […]
[…] […]
[…] […]