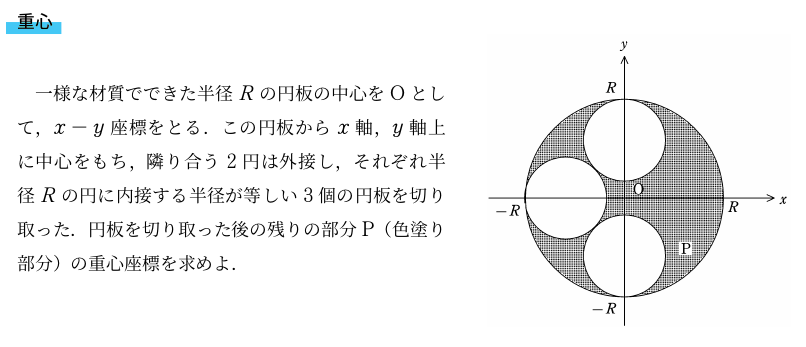
<問題>
<方針>
まず,対称性からPの重心は$x$軸上にあることがわかる.
切り取った1つの円板の半径$r$を求め,切り取った3つの円の重心の$x_{1},x_{2},x_{3}$,質量を$m$とする.また,Pの質量を$M$とし,重心座標を$X$とする.すべての重心の重心は原点になるから,$x$座標の重心の式
$0=\dfrac{MX+mx_{1}+mx_{2}+mx_{3}}{M+3m}$
より,$X$を求める.
<解答>
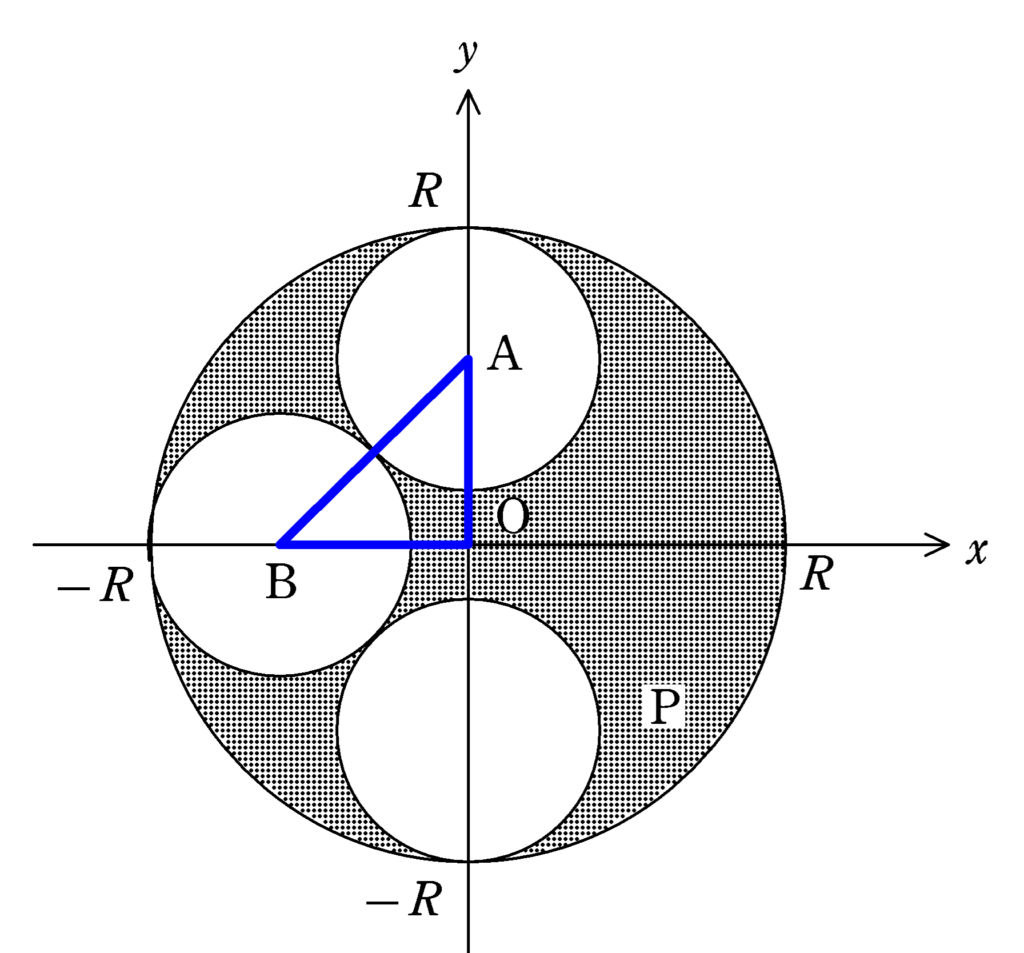
切り取った円の半径を$r$とする.すると,上図において,${\rm OA}={\rm OB}=R-r$であり,${\rm AB}=2r$であり,三角形$\rm OAB$は直角二等辺三角形であるから$\rm AB=\sqrt{2}OA$より
$2r=\sqrt{2}(R-r)$ $\,\,\therefore\,\, r=(\sqrt{2}-1)R$ $\cdots (\ast)$
切り取った円の面積は$\pi r^{2}$であるから,単位面積あたりの質量を$\rho$とおけば,切り取った円の質量$m$は
$m=\pi r^{2}\times \rho$
である.また,半径$R$の円の面積は$\pi R^{2}$なので,その質量は$\pi R^{2}\times \rho$だから,Pの質量$M$は
$M=\pi R^{2}\times \rho-3\pi r^{2}\times \rho=\pi\rho(R^{2}-3r^{2})$
である.また,切り取った3つの円の$x$座標はそれぞれ$0,0,-R+r$であり,切り取った3つの円板と残りのPの重心は切り取る前の円板の重心Oに等しいので,Pの重心の$x$座標を$X$として,重心の式より
座標$x_{1}$,$x_{2}$にそれぞれ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心の位置$x_{\rm G}$は
$x_{\rm G}=\dfrac{m_{1}x_{1}+m_{2}x_{2}}{m_{1}+m_{2}}$
※ これは,2つで考えたが,$n$個分に拡張できる.
$0=\dfrac{MX+m\times 0+m\times 0+m\times (-R+r)}{M+3m}$
$\therefore\,\, X=\dfrac{m(R-r)}{M}$
$M=\pi\rho(R^{2}-3r^{2})$,$m=\pi r^{2}\times \rho$を代入して
$X=\dfrac{\cancel{\pi} r^{2}\times \cancel{\rho}}{\cancel{\pi\rho}(R^{2}-3r^{2})}\times (R-r)$
ここで,$(\ast)$の$r=(\sqrt{2}-1)R$を代入すると割りと大変な目に合うので,$R=(\sqrt{2}+1)r$として,$R$を消去すると
$X=\dfrac{r}{2}$
を得る.ここに,$r=(\sqrt{2}-1)R$を代入して
$X=\dfrac{\sqrt{2}-1}{2}R$ (答)



コメント