
今回は電流と磁場の問題です.次のことを確認しましょう.
- 電流が流れるとまわりに磁場をつくる.
- 磁場中に電流が流れると力を受ける.
なんだかややこしい話ですね.問題の後に解説から書いてあるので,復習に使ってください.
解答は最後にまとめてあるので,チェックしてみてください!
図のように,十分長い直線導線1,2が空気中に固定されてあり,図の向きに電流$I_{1}$,$I_{2}$を流す.導線1,2の間に,導線3をおいて,電流$I_{3}$を流したところ,導線3にはたらく力の和は0となった.導線1と導線3の距離を$a$,導線2と導線3の距離を$b$,導線1,2,3は同一平面内にあるとして次の問いに答えよ.
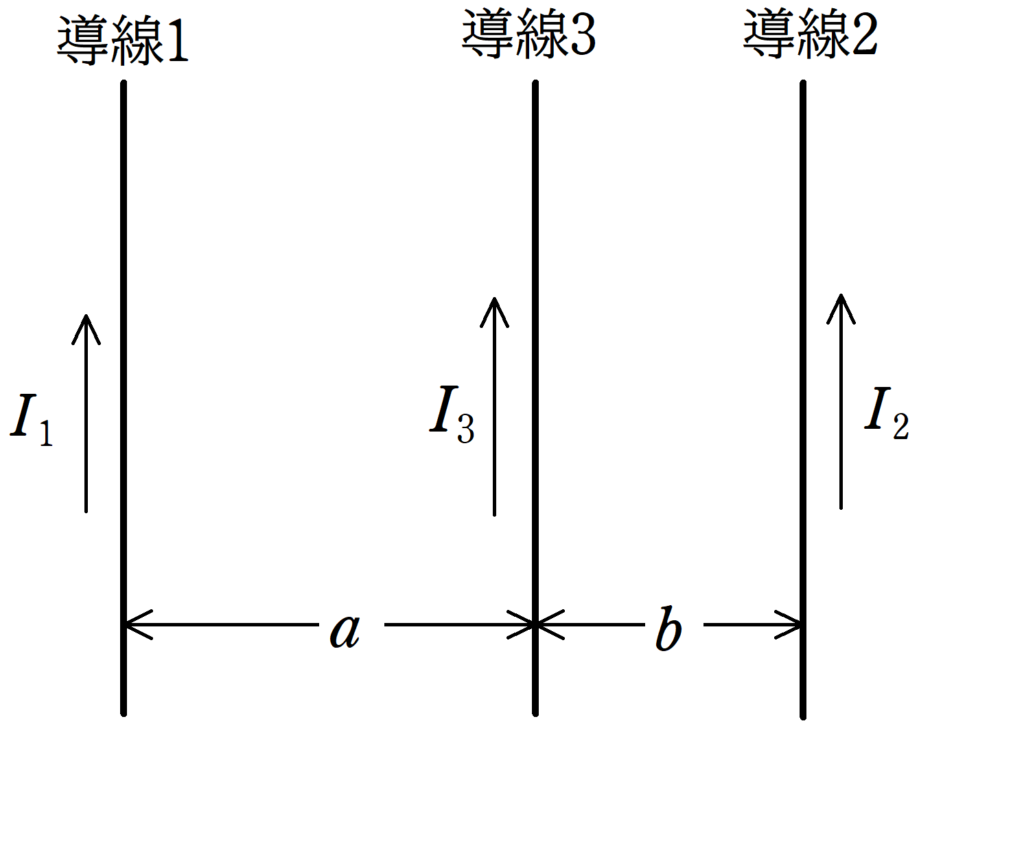
(1) 導線1に流れる電流が導線3の位置につくる磁場の大きさと向きについて,正しいものを次の中から選べ.
$① 大きさ:\dfrac{I_{1}}{2\pi a},向き:紙面手前から奥$
$② 大きさ:\dfrac{I_{1}}{2\pi a},向き:紙面奥から手前$
$③ 大きさ:\dfrac{I_{1}}{2\pi a},向き:左向き$
$④ 大きさ:\dfrac{I_{1}}{2\pi a},向き:右向き$
$⑤ 大きさ:\dfrac{I_{1}}{2a},向き:紙面手前から奥$
$⑥ 大きさ:\dfrac{I_{1}}{2a},向き:紙面奥から手前$
$⑦ 大きさ:\dfrac{I_{1}}{2a},向き:左向き$
$⑧ 大きさ:\dfrac{I_{1}}{2a},向き:右向き$
(2) $a , b , I_{1} , I_{2}$の関係として正しいものを次の中から選べ.
$① ab=I_{1}I_{2}$ $② aI_{1}=bI_{2}$ $③ bI_{1}=aI_{2}$ $④ a^{2}b^{2}=I_{1}I_{2}$
直線電流がつくる磁場
十分長い直線電流が距離$r$の位置につくる磁場$H_{1}$は,導線に流れる電流の大きさを$I_{1}$とすると
$H_{1}=\dfrac{I_{1}}{2\pi r}$
向きは右ねじの法則にしたがいます.
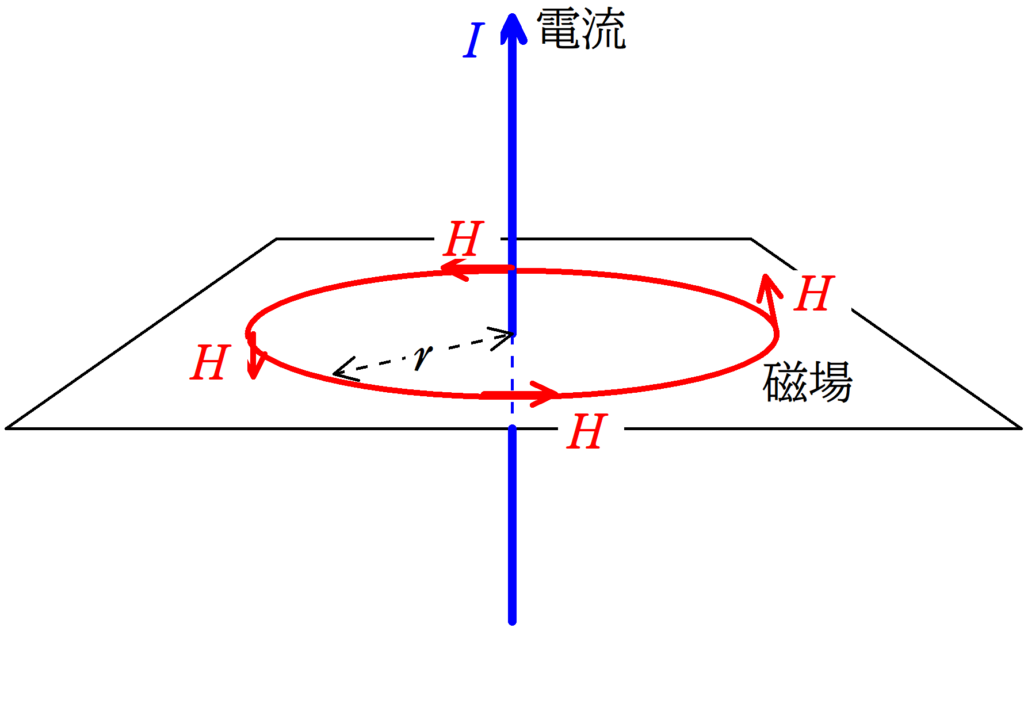
※ 右ねじの法則は右手の親指→電流,4本指→磁場 です.

電流を流すとまわりに磁場をつくります.
電流が大きいほど,大きな磁場をつくり,距離が近いところほど,大きな磁場をつくる式ですね.
さらに,磁場中を電流が流れると力を受けます.
ちなみに,高校で覚えておくべき磁場の公式は
- 十分長い直線電流がつくる磁場
- 円形電流が中心につくる磁場
- ソレノイドコイルに流す電流がコイル内部につくる磁場
の3つだけです.
電流が磁場から受ける力(電磁力)
電流の大きさを$I$,磁束密度の大きさを$B$とする.磁場の方向と電流の方向が垂直な関係にあるとき,導線の長さ$l$あたりにはたらく電磁力の大きさ$F$は
$F=IBl$
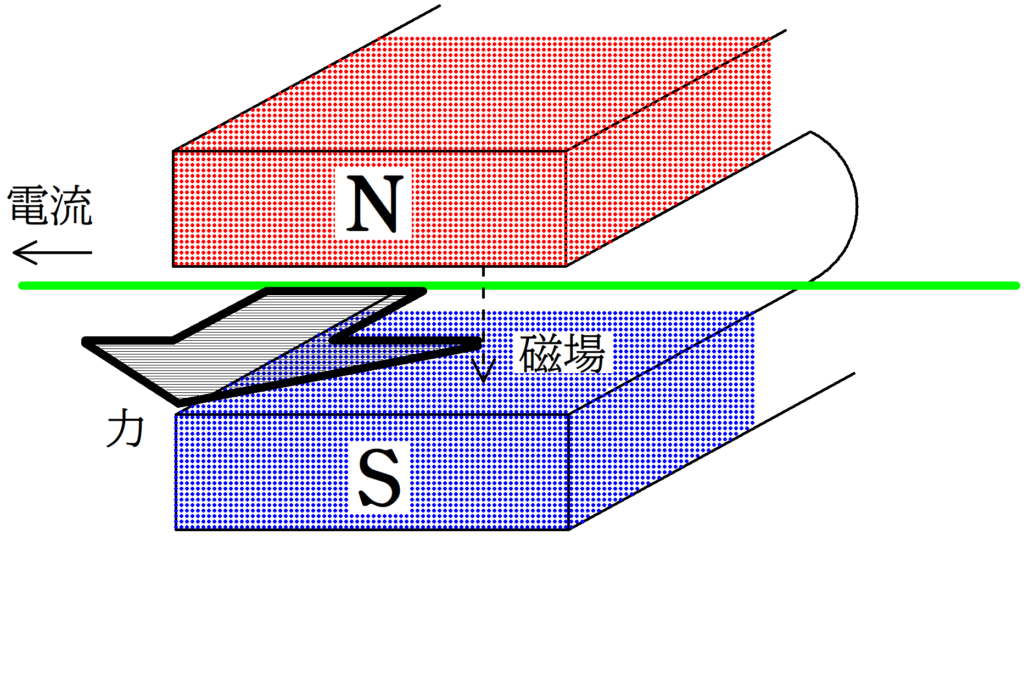
電磁力の向きはフレミング左手の法則にしたがいます.
※ 左手の親指→力の向き,人差し指→磁場の向き,中指→電流の向き

向きの間違いが割りと多いので注意してください!
(1)の解答
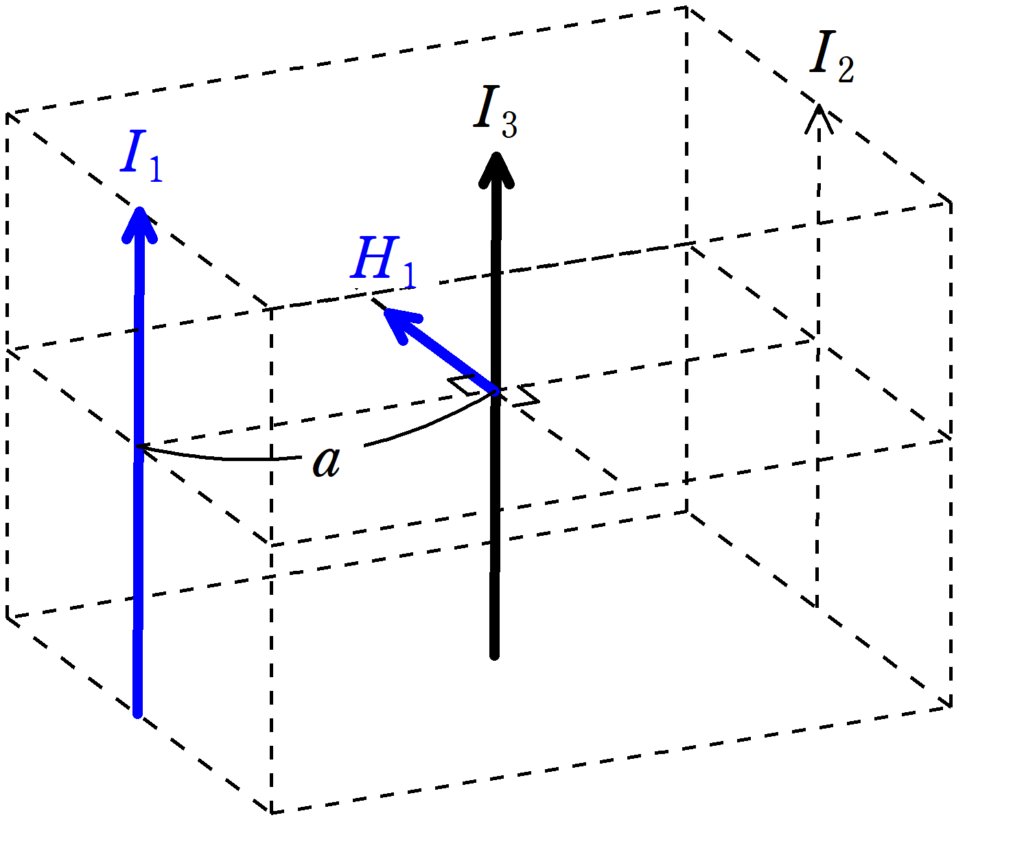
電流$I_{1}$が距離$a$の位置につくる磁場の大きさ$H_{1}$は
$H_{1}=\dfrac{I_{1}}{2\pi a}$
で,右ねじの法則を使えば,上図より,電流$I_{1}$が導線3の場所に作る磁場の向きは”紙面手前から奥方向”です.
したがって,答えは$①$.
(2)の解答
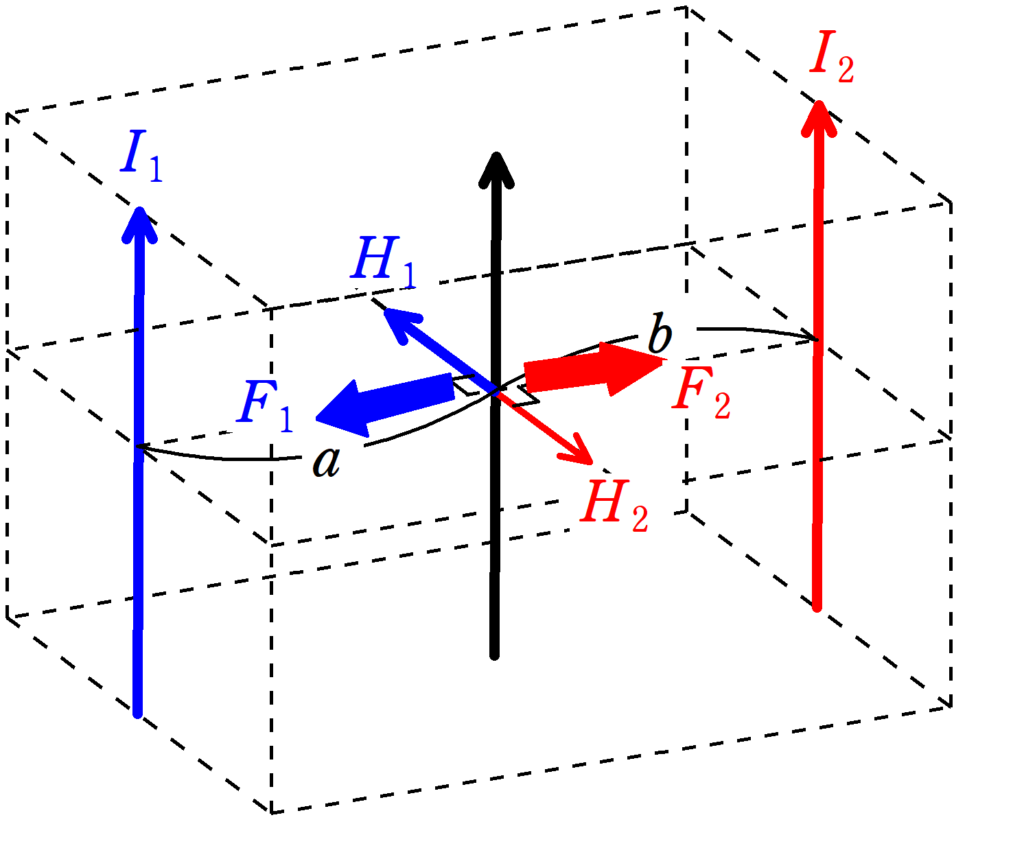
電流$I_{1}$と$I_{2}$が導線3の位置につくる磁場の向きは下図の$H_{1}$と$H_{2}$です.
それぞれの大きさは
$H_{1}=\dfrac{I_{1}}{2\pi a}$,$H_{2}=\dfrac{I_{2}}{2\pi b}$
となります.
そして,導線$I_{3}$が磁場$H_{1}$,$H_{2}$から受ける長さ$l$あたりのそれぞれの力の大きさを$F_{1}$,$F_{2}$とすると,フレミング左手の法則より,$F_{1}$と$F_{2}$は下図の向きにはたらきます.
ここで,磁束密度$B$と磁場$H$は透磁率を$\mu$とすると,次の関係があります.
磁束密度$B$と磁場$H$は,透磁率を$\mu$とすると
$B=\mu H$
の関係がある.
すると,電流$I_{1}$,$I_{2}$が導線3の位置につくる磁束密度$B_{1}$,$B_{2}$は透磁率を$\mu$とすると,それぞれ
$B_{1}=\mu H_{1}=\dfrac{\mu I_{1}}{2\pi a}$
$B_{2}=\mu H_{2}=\dfrac{\mu I_{2}}{2\pi b}$
したがって,長さ$l$あたりの電磁力の大きさ$F_{1}$,$F_{2}$は
$F_{1}=I_{3}B_{1}l=\dfrac{\mu I_{1}I_{3}l}{2\pi a}$
$F_{2}=I_{3}B_{2}l=\dfrac{\mu I_{2}I_{3}l}{2\pi b}$
問題の条件$F_{1}=F_{2}$より
$\eqalign{\dfrac{\mu I_{1}I_{3}l}{2\pi a}&=\dfrac{\mu I_{2}I_{3}l}{2\pi b}\cr \dfrac{I_{1}}{a}&=\dfrac{I_{2}}{b}\cr bI_{1}&=aI_{2}}$
したがって,答えは$③$です.
解答
解答
(1) $①$ (2) $③$

今回は電流どうしにはたらく力の問題でした!
基本問題だからこそ,確実にとりたい1問ですね!




コメント