
2つの物体が衝突する際に失われる運動エネルギーについて以下のことが成り立ちます.
質量$m_{1}$の物体1と質量$m_{2}$の物体2の1次元衝突を考える.
ただし,物体1と物体2を物体系としたときの外力からの撃力ははたらかないものとする.(たとえば,壁との衝突,床との衝突など)
物体1,物体2の衝突前の速度を$v_{1}$,$v_{2}$とし,はねかえり係数を$e$とするとき,衝突の前後での物体1と物体2の運動エネルギーの変化$\varDelta K$は,次のように表される.
$\varDelta K=-\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m_{2}}(1-e^{2})(v_{1}-v_{2})^{2}$

必ずしも覚えておくべき式でもないのですが,覚えておくと便利です.
導出していきましょう.
1.運動エネルギーを重心速度と重心からみた相対速度で表す
質量$m_{1}$の物体1と,質量$m_{2}$の物体2の速度をそれぞれ$v_{1}$,$v_{2}$とする.
このとき,運動エネルギーの和$K$は
$K=\dfrac{1}{2}m_{1}v_{1}^{2}+\dfrac{1}{2}m_{2}v_{2}^{2}$ $\dots (\ast)$

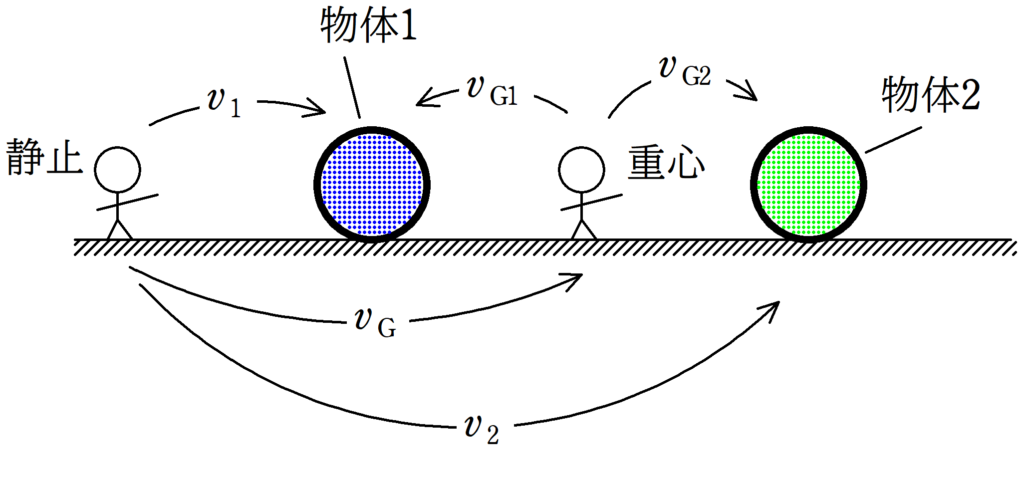
さらに,物体1と物体2の重心速度を$v_{\rm G}$とし,重心からみた物体1の速度を$v_{\rm G1}$,重心からみた物体2の速度を$v_{\rm G2}$とすると,
$v_{1}=v_{\rm G}+v_{\rm G1}$
$v_{2}=v_{\rm G}+v_{\rm G2}$
と表すことができます.
これを$(\ast)$に代入しましょう.
$\eqalign{K&=\dfrac{1}{2}m_{1}v_{1}^{2}+\dfrac{1}{2}m_{2}v_{2}^{2}\\&=\dfrac{1}{2}m_{1}(v_{\rm G}+v_{\rm G1})^{2}+\dfrac{1}{2}m_{2}(v_{\rm G}+v_{\rm G2})^{2}\\&=\dfrac{1}{2}m_{1}(v_{\rm G}^{2}+2v_{\rm G}v_{\rm G1}+v_{\rm G1}^{2})+\dfrac{1}{2}m_{2}(v_{G}^{2}+2v_{\rm G}v_{\rm G2}+v_{\rm G2}^{2})\\&=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+(m_{1}v_{\rm G1}+m_{2}v_{\rm G2})v_{\rm G}+\dfrac{1}{2}m_{1}v_{\rm G1}^{2}+\dfrac{1}{2}m_{2}v_{\rm G2}^{2} \dots (2\ast)}$

ここで,
重心からみた運動量の和は0
であることを利用して上式に代入しましょう.
「重心からみた運動量の和が0」であることはこちらの記事でも説明しています.
質量$m_{1}$,$m_{2}$の物体がある.
重心からみたそれぞれの速度を$v_{\rm G1}$,$v_{\rm G2}$とすると,次の式が成り立つ.
$m_{1}v_{\rm G1}+m_{2}v_{\rm G2}=0$
すなわち,重心からみた物体の運動量の和は0となる.

$(2\ast)$に$m_{1}v_{\rm G1}+m_{2}v_{\rm G2}=0$を代入しましょう.
$K=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}m_{1}v_{\rm G1}^{2}+\dfrac{1}{2}m_{2}v_{\rm G2}^{2} \dots (3\ast)$
2.運動エネルギーを重心速度と物体2に対する物体1の相対速度で表す

$v_{\rm G1}=v_{1}-v_{\rm G}$と$v_{\rm G2}=v_{2}-v_{\rm G}$に重心速度
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$
を代入しましょう.
速度$v_{1}$,$v_{2}$をもつ質量$m_{1}$,$m_{2}$の物体がある.
このときの重心速度$v_{\rm G}$は
$v_{\rm G}=\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}$
★ $v_{\rm G1}$について
$\eqalign{v_{\rm G1}&=v_{1}-v_{\rm G}\\&=v_{1}-\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\\&=\dfrac{(m_{1}+m_{2})v_{1}}{m_{1}+m_{2}}-\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\\&=\dfrac{m_{2}}{m_{1}+m_{2}}(v_{1}-v_{2}) \dots (4\ast)}$
★ $v_{\rm G2}$について
$\eqalign{v_{\rm G2}&=v_{2}-v_{\rm G}\\&=v_{2}-\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\\&=\dfrac{(m_{1}+m_{2})v_{2}}{m_{1}+m_{2}}-\dfrac{m_{1}v_{1}+m_{2}v_{2}}{m_{1}+m_{2}}\\&=-\dfrac{m_{1}}{m_{1}+m_{2}}(v_{1}-v_{2}) \dots (5\ast)}$

$(4\ast)$,$(5\ast)$を$(3\ast)$に代入しましょう.
$\eqalign{K&=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}m_{1}v_{\rm G1}^{2}+\dfrac{1}{2}m_{2}v_{\rm G2}^{2}\\&=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}m_{1}\{\dfrac{m_{2}}{m_{1}+m_{2}}(v_{1}-v_{2})\}^{2}+\dfrac{1}{2}m_{2}\{-\dfrac{m_{1}}{m_{1}+m_{2}}(v_{1}-v_{2})\}^{2}\\&=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}\dfrac{m_{1}m_{2}^{2}}{(m_{1}+m_{2})^{2}}(v_{1}-v_{2})^{2}+\dfrac{1}{2}\dfrac{m_{1}^{2}m_{2}}{(m_{1}+m_{2})^{2}}(v_{1}-v_{2})^{2}\\&=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}\dfrac{m_{1}m_{2}}{(m_{1}+m_{2})^{2}}(m_{1}+m_{2})(v_{1}-v_{2})^{2}\\&=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(v_{1}-v_{2})^{2}}$
3.運動エネルギーの変化を計算する

ここで,重心速度$v_{\rm G}$は衝突の際に物体系外から撃力がはたらかない限り,変化しません.
重心速度が変化するときは,重心加速度が0でないときです.
重心加速度は次の式で求めることができます.
質量$m_{1}$,$m_{2}$の物体の重心の加速度を$a_{\rm G}$とする.2つの物体にはたらいている力をそれぞれ$F_{1}$,$F_{2}$とすると,次の式が成り立つ.
$(m_{1}+m_{2})a_{\rm G}=F_{1}+F_{2}$

この式より,力の和が0のとき(または,力がはたらいても,衝突直前後の非常に短い時間であれば,速度変化は無視できます.)は,重心速度が変化しません.
$K=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(v_{1}-v_{2})^{2}$ $\dots (6\ast)$

衝突後の物体1と物体2の速度を$v_{1}^{\prime}$,$v_{2}^{\prime}$であるとき,重心速度は変化しないとして,物体1と物体2の運動エネルギーの和$K^{\prime}$は次のようになります.
$K^{\prime}=\dfrac{1}{2}(m_{1}+m_{2})v_{\rm G}^{2}+\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(v_{1}^{\prime}-v_{2}^{\prime})^{2}$ $\dots (7\ast)$

したがって,運動エネルギーの変化$\varDelta K$は次のようになります.
$\eqalign{\varDelta K&=K^{\prime}-K\\&=\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(v_{1}^{\prime}-v_{2}^{\prime})^{2}-\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(v_{1}-v_{2})^{2}\\&=\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}\{(v_{1}^{\prime}-v_{2}^{\prime})^{2}-(v_{1}-v_{2})^{2}\} \dots (8\ast)}$

さらに,はねかえり係数$e$の定義より
$e=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$
これを変形して
$v_{1}^{\prime}-v_{2}^{\prime}=-e(v_{1}-v_{2})$
$(8\ast)$に代入します.
$\eqalign{\varDelta K&=\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}\{(v_{1}-v_{2})^{2}e^{2}-(v_{1}-v_{2})^{2}\}\\&=\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(e^{2}-1)(v_{1}-v_{2})^{2}\\&=-\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(1-e^{2})(v_{1}-v_{2})^{2}}$

この式より,$e=0$の完全非弾性衝突の際の運動エネルギーの変化$\varDelta K$は
$\varDelta K=-\dfrac{1}{2}\dfrac{m_{1}m_{2}}{m_{1}+m{2}}(v_{1}-v_{2})^{2}$
となり,力学的エネルギーは必ず減少します.
実際の共通テストの問題では,時間制限もあるため,完全弾性衝突以外の衝突では運動エネルギーが失われるということは知識で解く必要があったかと思います.

コメント
[…] 2021年 共通テスト第4問A問3 衝突によって失われるエネルギー […]