
2021年共通テスト第2問題Aは抵抗とコンデンサーの回路の問題でした.
選択肢は用意していませんが,次の問題を解いてみましょう.
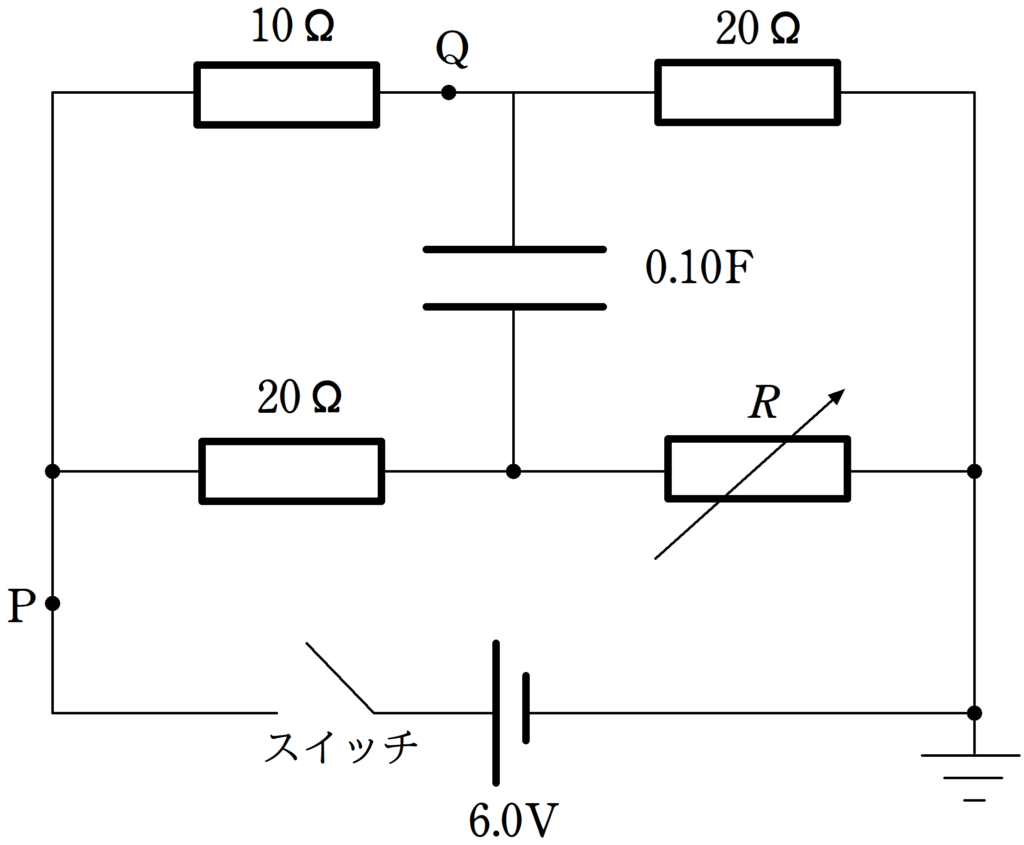
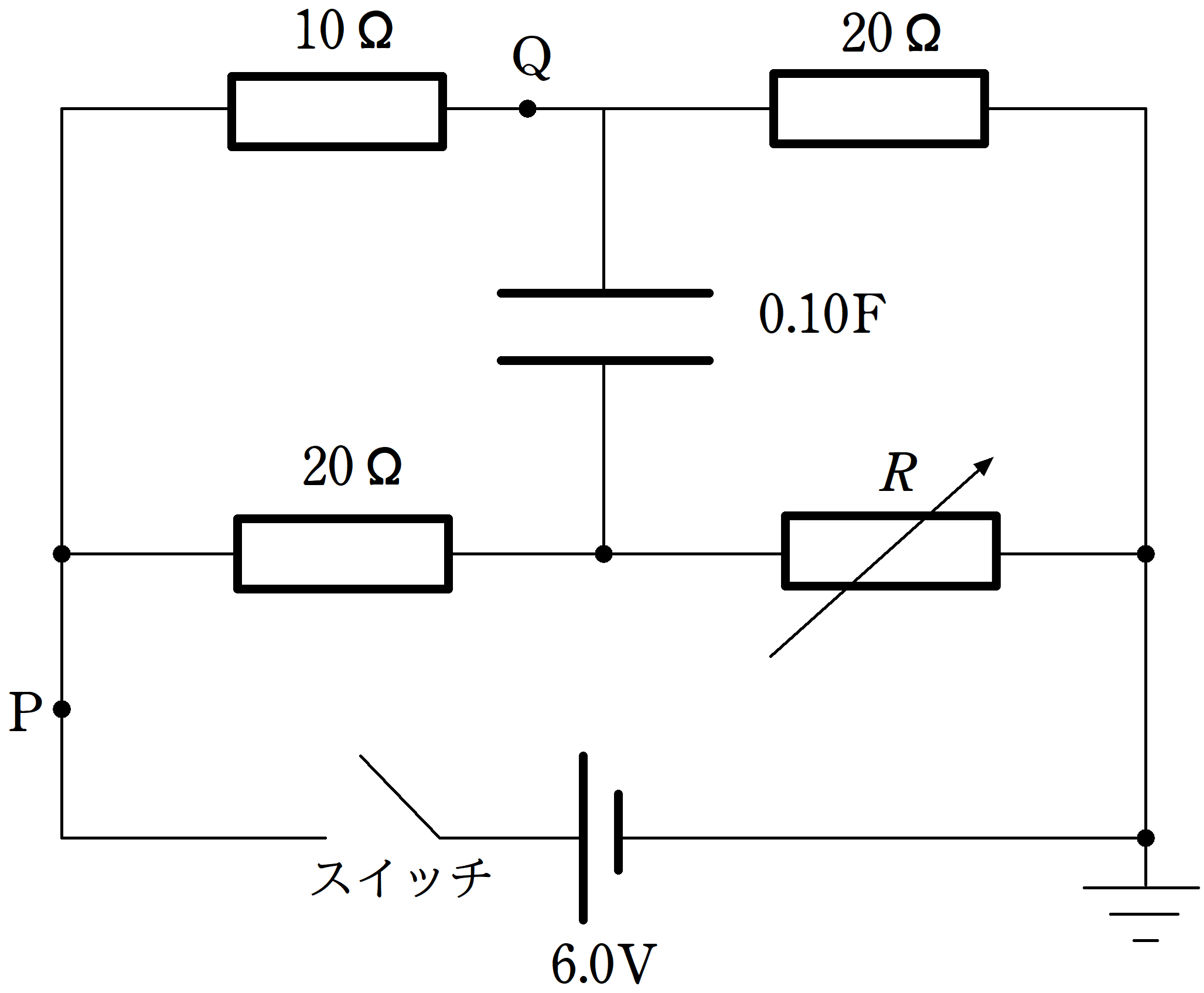
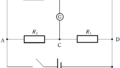
上図のように,抵抗値が$10\Omega$と$20\Omega$の抵抗,抵抗値$R$を自由に変えられる可変抵抗,電気容量が$0.10\rm F$のコンデンサー,スイッチおよび電圧が$6.0\rm V$の直流電源からなる回路がある.最初スイッチは開いており,コンデンサーは充電されていないとする.
(1) 可変抵抗の抵抗値を$R=10\Omega$に設定する.スイッチを閉じた瞬間に点$\rm Q$を流れる電流の大きさを有効数字2桁で求めよ.
(2) 可変抵抗の抵抗値は$R=10\Omega$にしたまま,スイッチを閉じて十分時間が経過すると,コンデンサーに流れ込む電流は0となる.このとき,図の$\rm P$を流れる電流の大きさと,コンデンサーに蓄えられた電気量をそれぞれ有効数字2桁で求めよ.
(3) スイッチを開いてコンデンサーに蓄えられた電荷を完全に放電させた.次に,可変抵抗の抵抗値を変え,再びスイッチを入れた.その後,点$\rm P$を流れる電流はスイッチを入れた直後の値を保持した.可変抵抗の抵抗値$R$を有効数字2桁で表せ.
<解答>
(1)
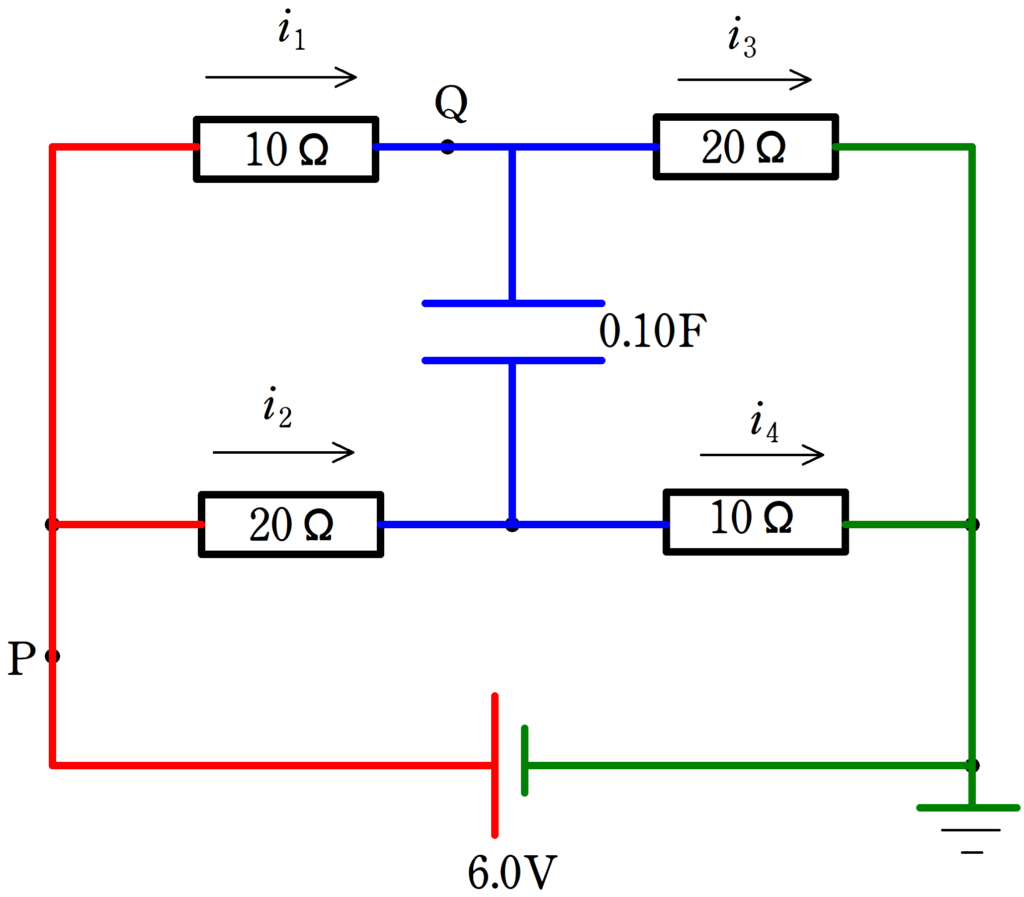

スイッチを閉じた直後,コンデンサーには電荷が蓄えられていないため,コンデンサー間の電位差は0です.
各抵抗に流れる電流を$i_{1}$,$i_{2}$,$i_{3}$,$i_{4}$で設定しました.
ここで注意して欲しいのが,$i_{1}\neq i_{3}$であるということです.(もちろん,$i_{2}\neq i_{4}$でもあります.)
コンデンサーにも電流が流れていることに注意しましょう.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.

ただ,あまりにも文字をたくさん設定すると計算が面倒なので,次のように工夫をするとよいです.
オームの法則は,
抵抗間の電位差=抵抗×抵抗に流れる電流
です.
$i_{1}$と$i_{2}$が流れている抵抗の電圧は等しいので,次の関係が成り立ちます.
抵抗×電流=一定
つまり,
$10i_{1}=20i_{2}$
$\therefore i_{2}=\dfrac{i_{1}}{2}$ $\dots (\ast)$
となります.
また,キルヒホッフ第1法則を考えれば,
$i_{1}+i_{2}=i_{3}+i_{4}$ $\dots (2\ast)$
が成り立ちます.
そして,同様に$i_{3}$と$i_{4}$が流れている抵抗の電圧は等しいので
$20i_{3}=10i_{4}$
$\therefore i_{3}=\dfrac{i_{4}}{2}$ $\dots (3\ast)$
$(\ast)$,$(3\ast)$を$(2\ast)$に代入して
$\eqalign{i_{1}+\dfrac{i_{1}}{2}&=\dfrac{i_{4}}{2}+i_{4}\cr i_{1}&=i_{4}}$
つまり,$i_{1}=i_{4}=i$とおけば,$i_{2}=i_{3}=\dfrac{i}{2}$とおけます.
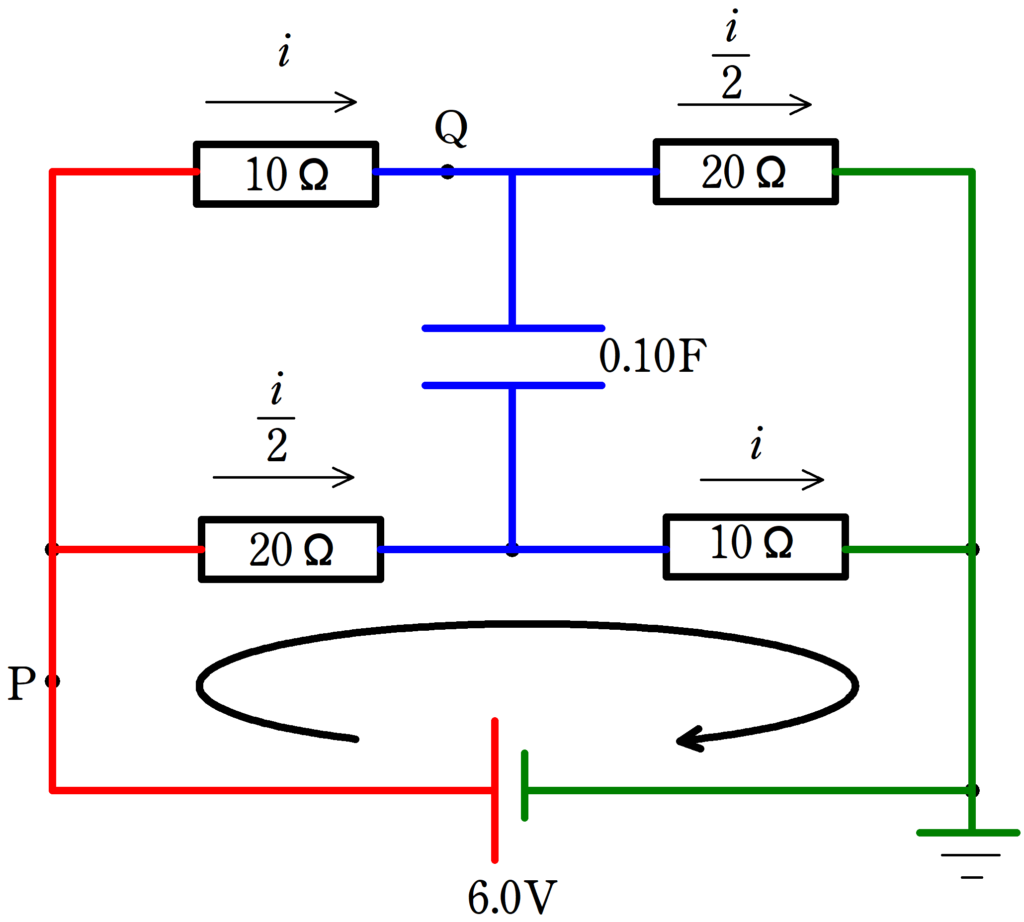

電圧降下の式を立てて$i$を求めましょう.
電位は上図の矢印のように追いましょう.
★ キルヒホッフ則(電圧降下の式)
$6.0-20\cdot \dfrac{i}{2}-10i=0$
$i=0.30 \rm A$ (答)
(2)
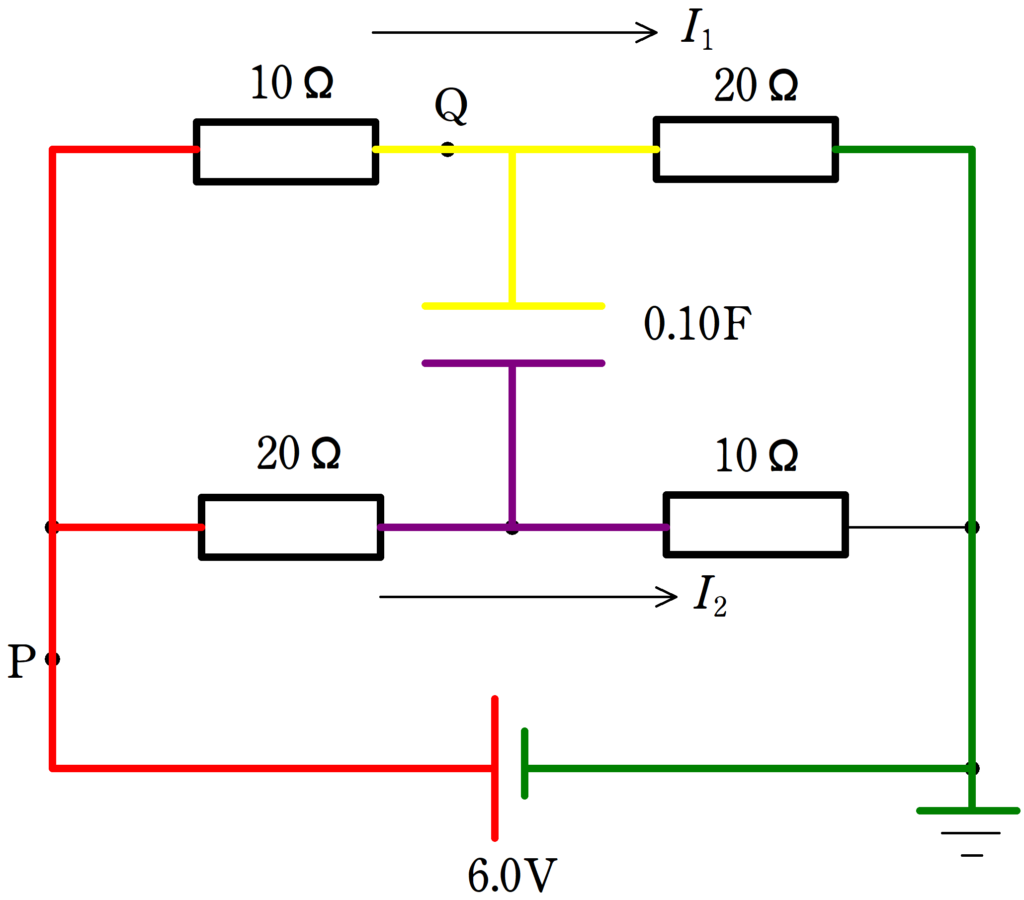

スイッチを入れて十分時間が経つと,コンデンサーには電流が流れません.
その結果,上図のように電流$I_{1}$,$I_{2}$が設定できます.
外回りと内回りそれぞれのキルヒホッフ則を立ててみましょう.
★ キルヒホッフ則(電圧降下の式)
$6.0-10I_{1}-20I_{1}=0$ $\therefore I_{1}=0.20 \rm A$
$6.0-20I_{2}-10I_{2}=0$ $\therefore I_{2}=0.20 \rm A$
したがって,点$\rm P$を流れる電流$I_{\rm P}$は
$I_{\rm P}=I_{1}+I_{2}=0.40 \rm A$ (答)
上図の黄色の部分の電位を基準の$0 \rm V$として,黄色部分の電位を$V_{1}$,紫色部分の電位を$V_{2}$とすると
$V_{1}=6.0-10\cdot 0.20=4.0 \rm V$
$V_{2}=6.0-20\cdot 0.20=2.0 \rm V$
したがって,コンデンサー間の電位差$\varDelta V$は
$\varDelta V=V_{1}-V_{2}=2.0 \rm V$
したがって,コンデンサーの基本式より,蓄えられた電気量$Q$は
$Q=0.10\cdot 2.0=0.20 \rm C$ (答)
(3)

最後は少し意図が読みにくいかもしれません.
スイッチを入れても電流の大きさが変化しないということは,コンデンサーに電流が流れないということです.
コンデンサーに電流が流れてしまうと,コンデンサーに電圧が生じて,電流は変化してしまいます.
そこで,次のホイートストンブリッジ回路の条件を使うと問題が簡単に解けます.
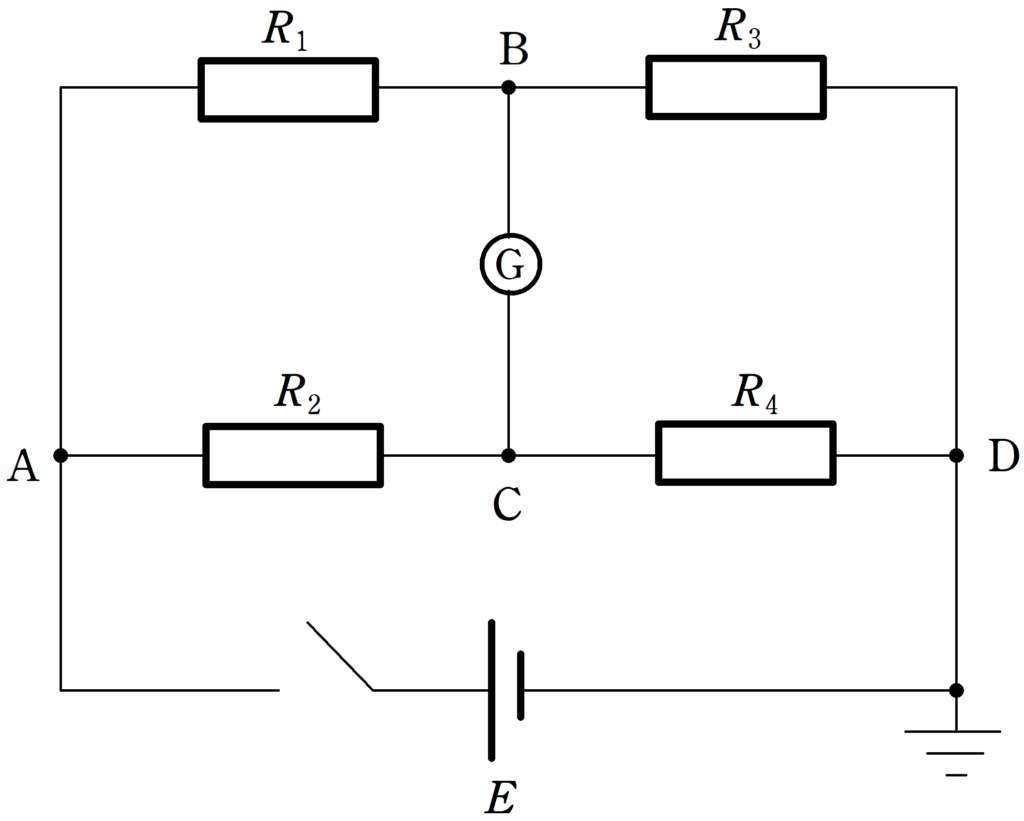
上図に回路において,スイッチを閉じたときに検流計に電流が流れなかった.
このとき,抵抗$R_{1}$,$R_{2}$,$R_{3}$,$R_{4}$の間に次の関係が成り立つ.
$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$
逆に,上の抵抗の関係式が成り立つのであれば,検流計に電流は流れない.

ホイートストンブリッジ回路の条件はこちらです.
この条件を用いれば
$\dfrac{10}{20}=\dfrac{20}{R}$
$\therefore R=40\Omega$ (答)

基本がわかっていれば確実に解ける問題だね.

コメント