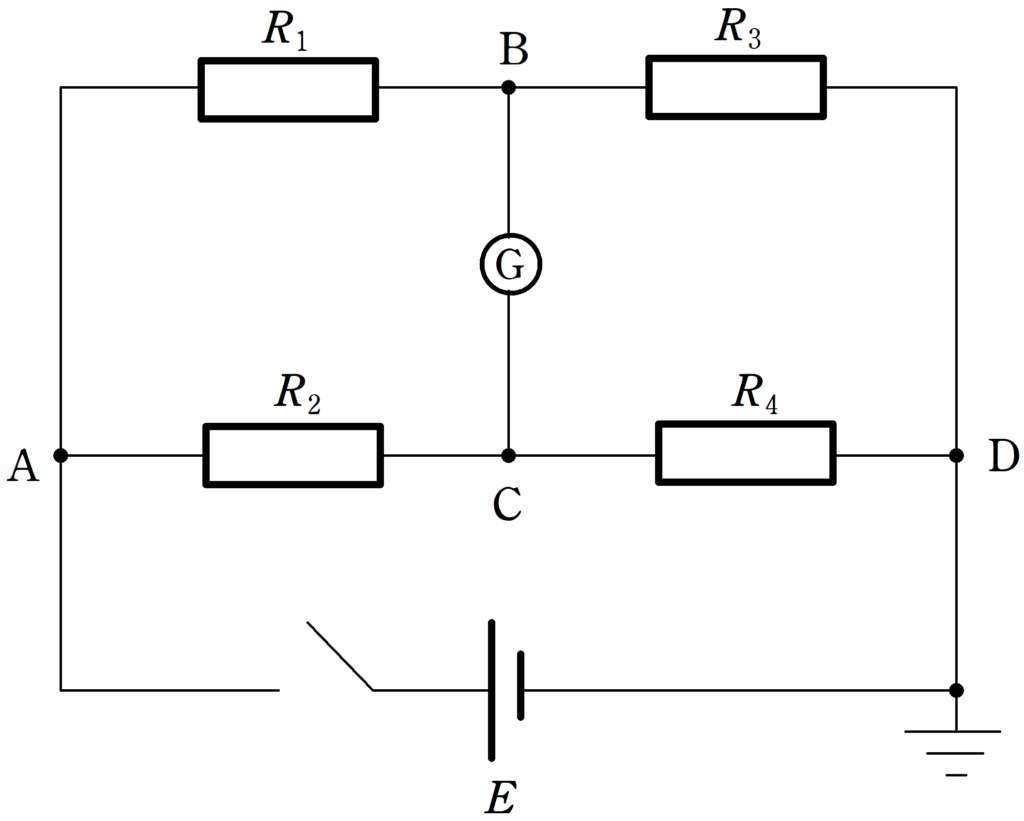
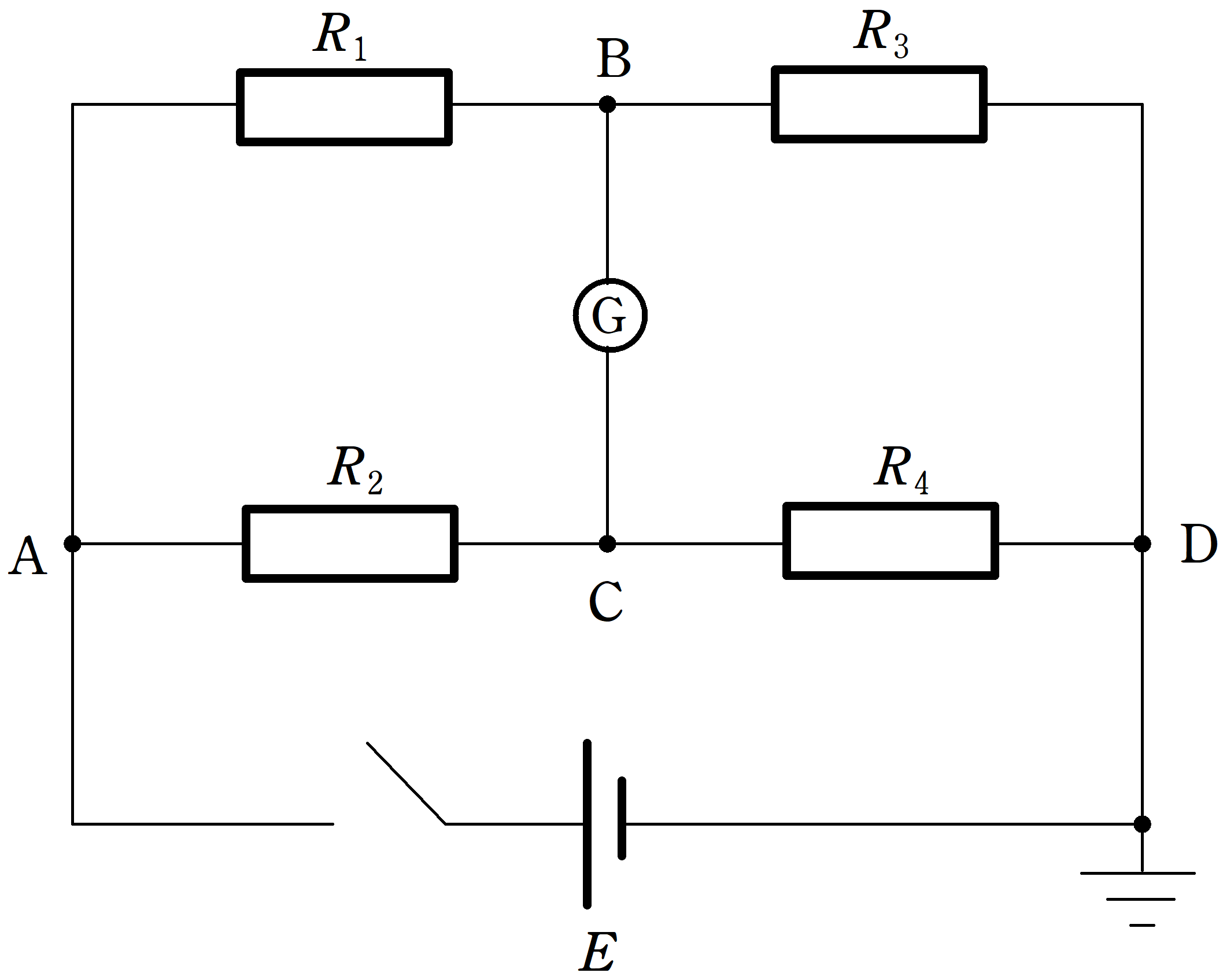
上図に回路において,スイッチを閉じたときに検流計に電流が流れなかった.
このとき,抵抗$R_{1}$,$R_{2}$,$R_{3}$,$R_{4}$の間に次の関係が成り立つ.
$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$
($R_{1}R_{4}=R_{2}R_{3}$)
逆に,上の抵抗の関係式が成り立つのであれば,検流計に電流は流れない.

今回は,このホイートストンブリッジ回路の平衡条件の証明をしていきます.
検流計に電流が流れない$\Longrightarrow$$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$
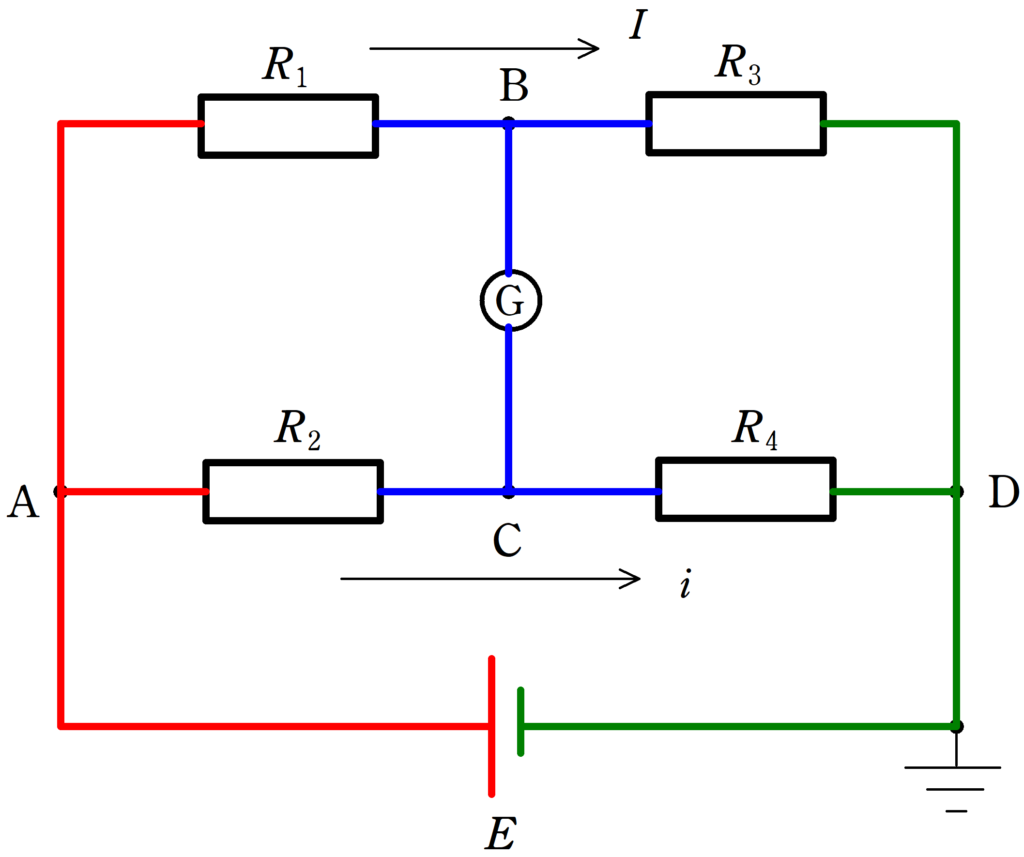

検流計に電流が流れないとき,次の3つの条件を使うことができます.
1. $R_{1}$と$R_{3}$に流れる電流は同じ.
2. $R_{2}$と$R_{4}$に流れる電流は同じ.
3. BC間の電位差は0

1.と2.の条件から上図のように,抵抗$R_{1}$と$R_{3}$に流れる電流を$I$,抵抗$R_{2}$と$R_{4}$を流れる電流を$i$とおくことができます.
さらに,BC間の電位差が0であることから,次の2つのことが言えます.
- AB間の電位差とAC間の電位差が同じ
- BD間の電位差とCD間の電位差が同じ
この2つの条件を式にしてみましょう.
★ AB間の電位差とAC間の電位差が同じ
$R_{1}I=R_{2}i$
$\therefore \dfrac{i}{I}=\dfrac{R_{1}}{R_{2}}$ $\dots (\ast)$
★ BD間の電位差とCD間の電位差が同じ
$R_{3}I=R_{4}i$
$\therefore \dfrac{i}{I}=\dfrac{R_{3}}{R_{4}}$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より
$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$
$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$$\Longrightarrow$検流計に電流が流れない
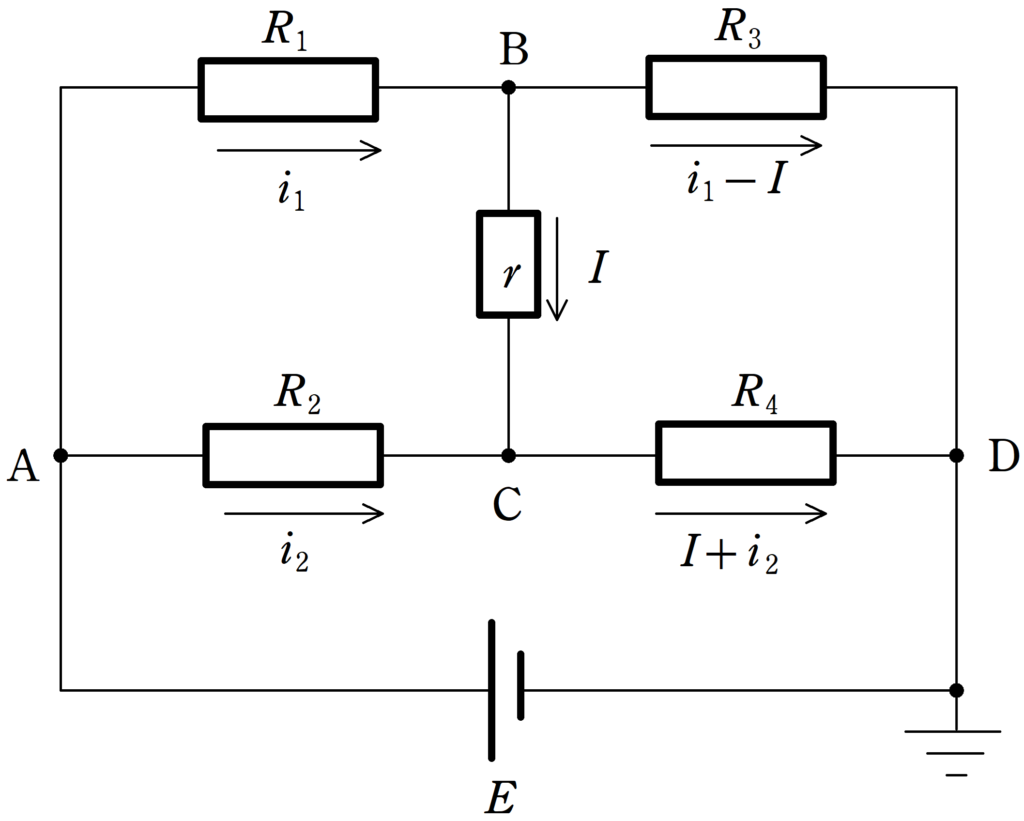

$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$が成り立つときに,$\rm BC$間に電流が流れないことを示しましょう.
上図のように,抵抗$R_{1}$に流れる電流を$i_{1}$,$R_{2}$に流れる電流を$i_{2}$,検流計の内部抵抗を$r$として,$\rm BC$間に流れる電流を$I$と設定しましょう.
キルヒホッフ第1法則を考えれば,$R_{3}$に流れる電流は$i_{1}-I$,$R_{4}$に流れる電流は$I+i_{2}$となります.
最終目標は$I=0$を示すことです.
それでは,次の3つの経路のキルヒホッフ則(電圧降下の式)を立てましょう.
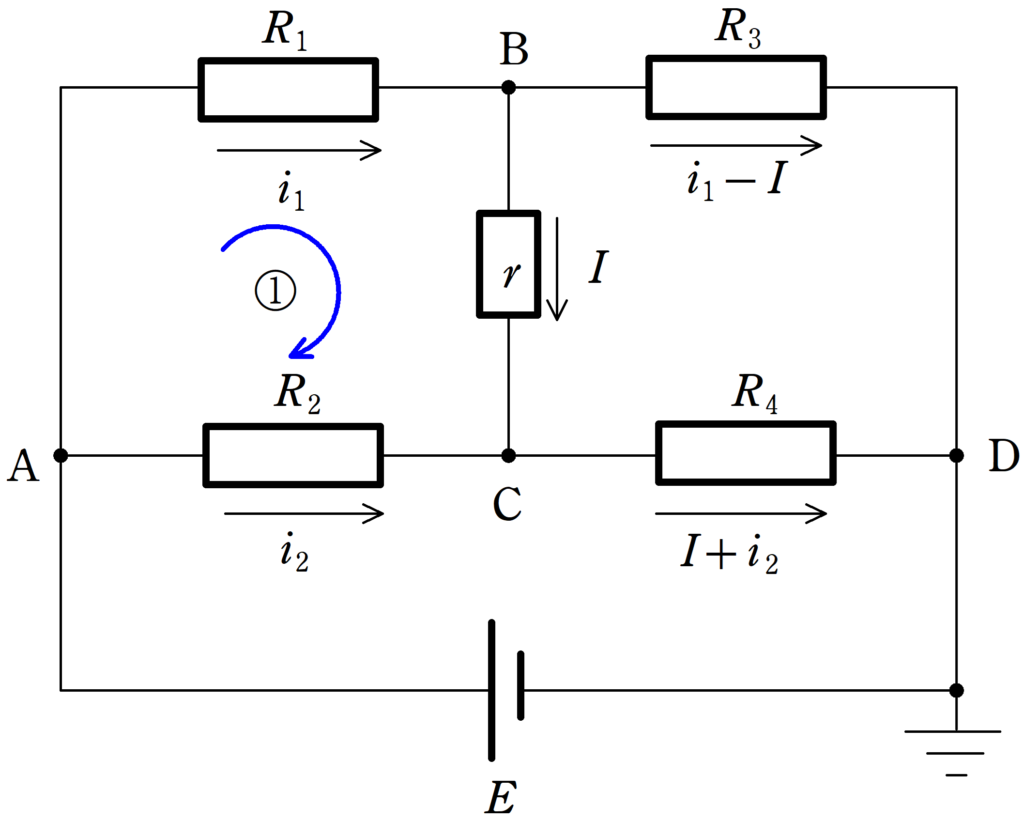
★ ①のキルヒホッフ則
$E-R_{1}i_{1}-rI+R_{2}i_{2}=E$
$\therefore$ $R_{1}i_{1}-R_{2}i_{2}+rI=0$ $\dots (3\ast)$
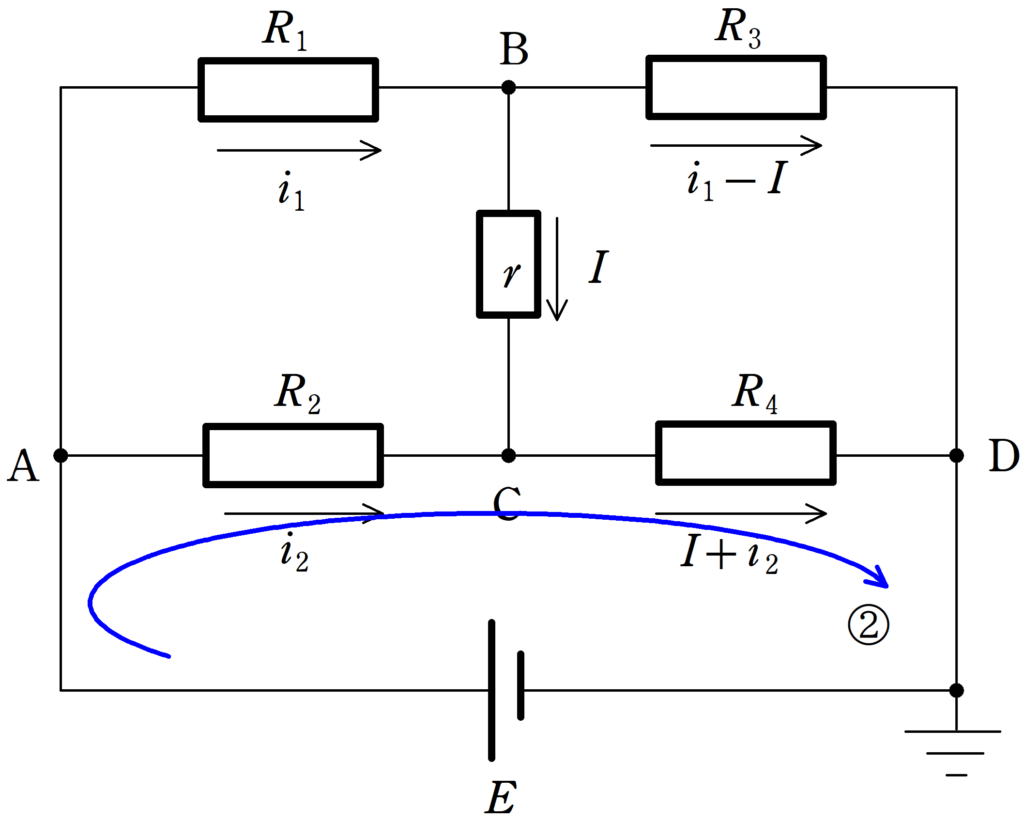
★ ②のキルヒホッフ則
$\eqalign{E-R_{2}i_{2}-R_{4}(I+i_{2})&=0\cr (R_{2}+R_{4})i_{2}&=E-R_{4}I\cr i_{2}&=\dfrac{E-R_{4}I}{R_{2}+R_{4}} \dots (4\ast)}$
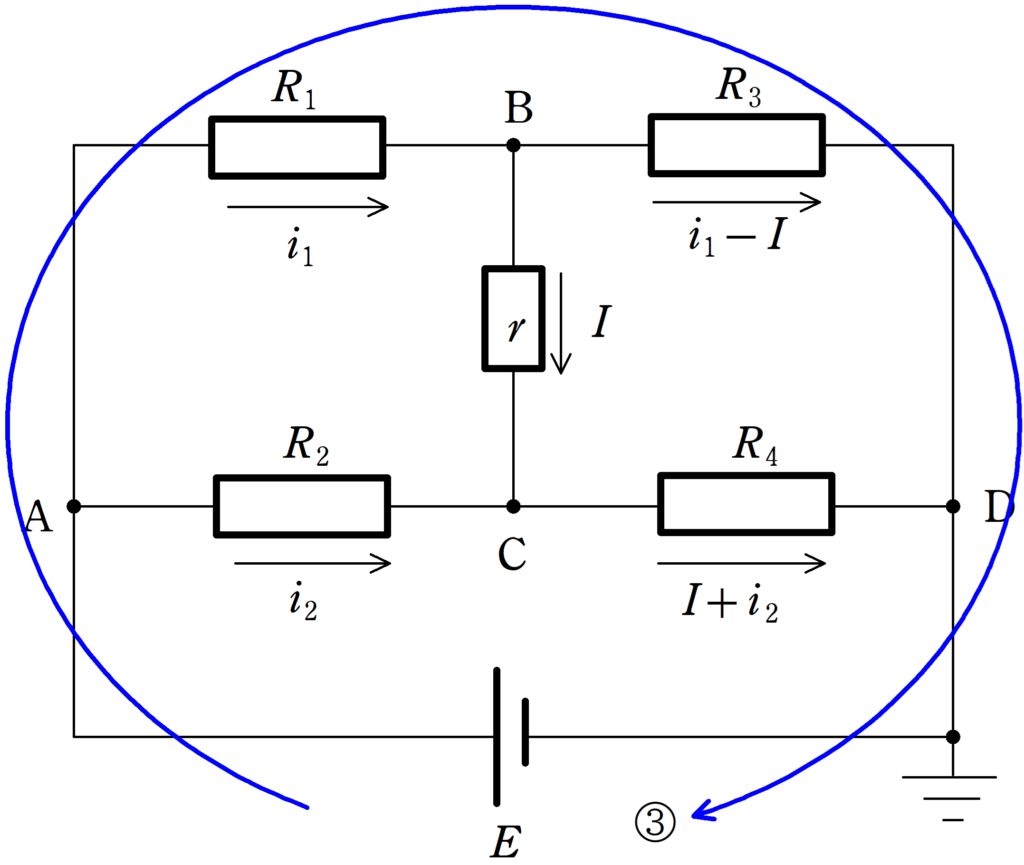
★ ③のキルヒホッフ則
$\eqalign{E-R_{1}i_{1}-R_{3}(i_{1}-I)&=0\cr (R_{1}+R_{3})i_{1}&=E+R_{3}I\cr i_{1}&=\dfrac{E+R_{3}I}{R_{1}+R_{3}} \dots (5\ast)}$
$(4\ast)$の$i_{2}=\dfrac{E-R_{4}I}{R_{2}+R_{4}}$と$(5\ast)$の$i_{1}=\dfrac{E+R_{3}I}{R_{1}+R_{3}}$を$(3\ast)$の$R_{1}i_{1}-R_{2}i_{2}+rI=0$に代入すると
$R_{1}\cdot \dfrac{E+R_{3}I}{R_{1}+R_{3}}-R_{2}\cdot \dfrac{E-R_{4}I}{R_{2}+R_{4}}+rI=0$ $\dots (6\ast)$

さて,ここで$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}$を使いましょう.
$\dfrac{R_{1}}{R_{2}}=\dfrac{R_{3}}{R_{4}}=k$
とおくと,
$R_{1}=kR_{2}$,$R_{3}=kR_{4}$
となります.
これらを$(6\ast)$に代入します.
$\eqalign{\cancel{k}R_{2}\cdot \dfrac{E+kR_{4}I}{\cancel{k}R_{2}+\cancel{k}R_{4}}-R_{2}\cdot \dfrac{E-R_{4}I}{R_{2}+R_{4}}+rI&=0\cr \cancel{\dfrac{R_{2}E}{R_{2}+R_{4}}}+\dfrac{kR_{2}R_{4}}{R_{2}+R_{4}}I-\cancel{\dfrac{R_{2}E}{R_{2}+R_{4}}}+\dfrac{R_{2}R_{4}}{R_{2}+R_{4}}I+rI&=0\cr (\dfrac{kR_{2}R_{4}}{R_{2}+R_{4}}+\dfrac{R_{2}R_{4}}{R_{2}+R_{4}}+r)I&=0}$
$\dfrac{kR_{2}R_{4}}{R_{2}+R_{4}}+\dfrac{R_{2}R_{4}}{R_{2}+R_{4}}+r\neq 0$より,$I=0$.

こっちの方がよく使うイメージだけど,割と面倒な計算になるんだね.
これは覚えておいた方がいいな..


コメント
[…] […]
[…] […]
[…] […]