
今回は,東工大の有名問題を扱います.
簡単なところは省いてあります.
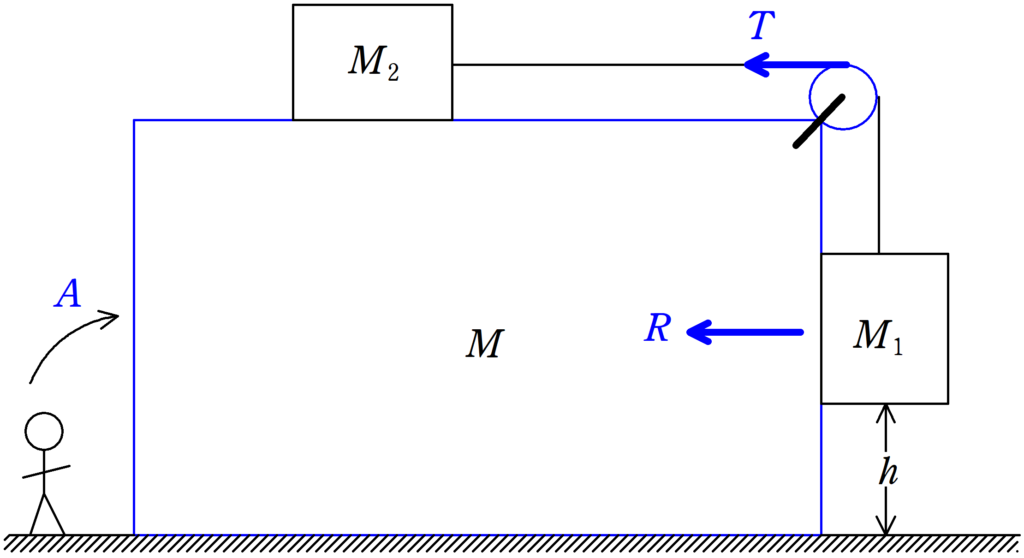
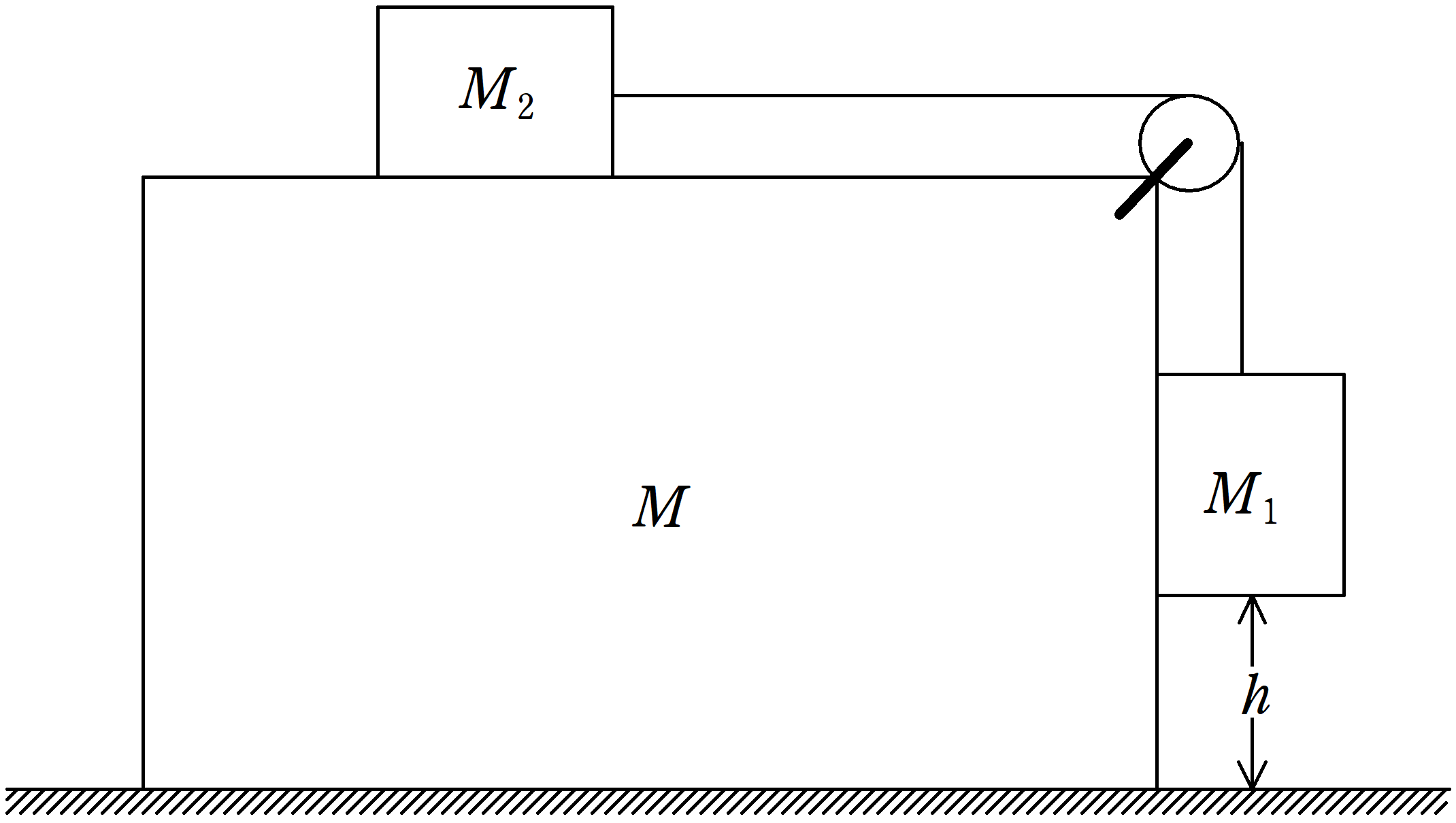
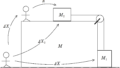
図に示すように質量$M$の直方体が水平面上に置かれている.$M$の上に置かれた質量$M_{2}$の物体から水平面に張ったひもを滑車にかけ,その先端に質量$M_{1}$の物体を鉛直につり下げる.$M_{1}$の側面は$M$と接し,上下になめらかなにすべることができるが,離れないような構造になっている.ただし,ひもは伸びず,その質量は無視できる.また,重力加速度は$g$である.
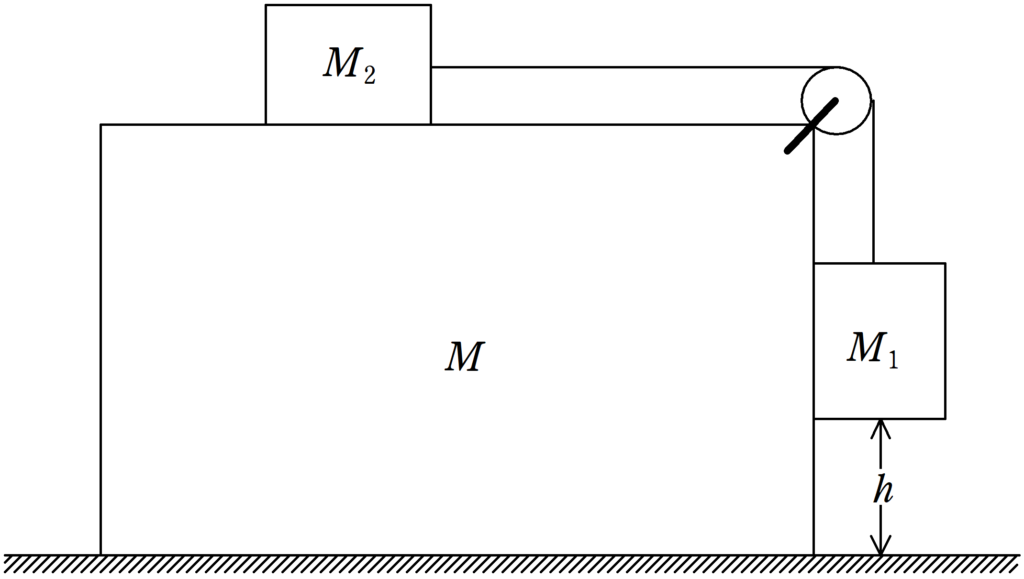
問 $M_{2}$と$M$の間および$M$と水平面の間に摩擦がないものとし,$M_{1}$の底面の高さが$h$になるように$M_{2}$と$M$をおさえた状態から手をはなした.$M_{1}$が水平面に達するまでの間に$M$が動く距離$x$を求めよ.
<解法1> 加速度を求めて解く.

運動方程式を立てて,加速度を求めます.
運動方程式は次の手順で立式します.
- 運動方程式を立てる”対象物体“,”座標の向き“,”観測者“を決める.
- 1.で決定した座標の向きを加速度の向きにする.
- 1.で決めた対象物体にはたらく力(相手から受ける力のみ.)をすべてかき,2.で決めた加速度の向きとそれに対して垂直な方向に力を分解する.
- 1.で決めた観測者が加速度運動している際は慣性力を忘れずに.
- 2.で決めた加速度の向きにそれぞれ運動方程式を立てる.

物体Aが運動していて,物体Aの上をさらに物体Bが運動している問題はよくみかけると思います.
このとき,物体Bの運動は物体Aの上の観測者からみるとシンプルになることが多いです.
今回も質量$M_{1}$と$M_{2}$の運動は,質量$M$の物体からみるとよいでしょう.
質量$M$の物体の上からみると,質量$M_{1}$と質量$M_{2}$の加速度は向きこそ違いますが,大きさは同じとみることができます.
逆に,水平面上で静止している人から見ると,質量$M_{2}$は複雑な運動をします.
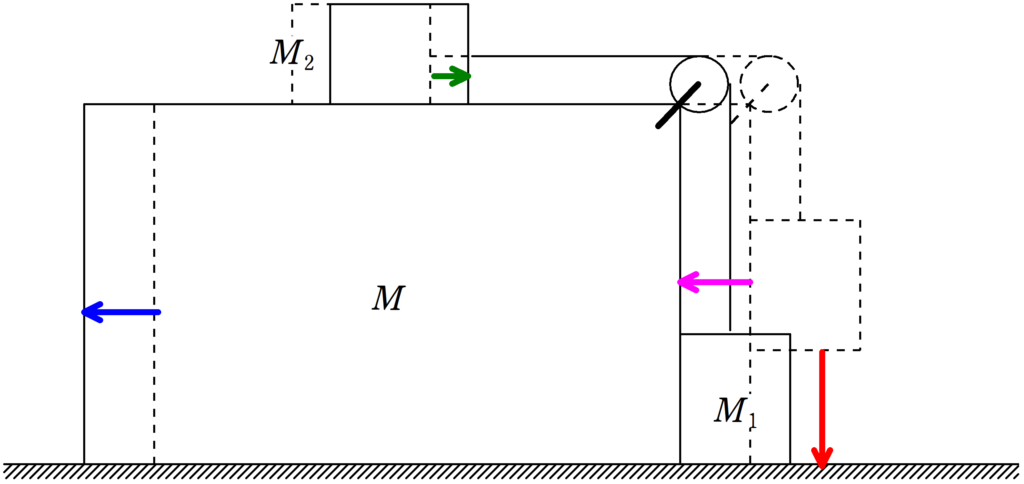

それでは,力を図示しましょう.
質量$M$と質量$M_{2}$の物体は水平方向にしか運動していないので,水平方向の力のみ,質量$M_{1}$の物体は水平方向と鉛直方向に動いているので,水平方向の鉛直方向の力をかきます.(摩擦力がはたらく際は,水平方向のみの運動でも鉛直方向の力を図示します.)
力をもれなくえがくためには,接触部分に着目します.
次の①~⑥の接触部分に着目します.
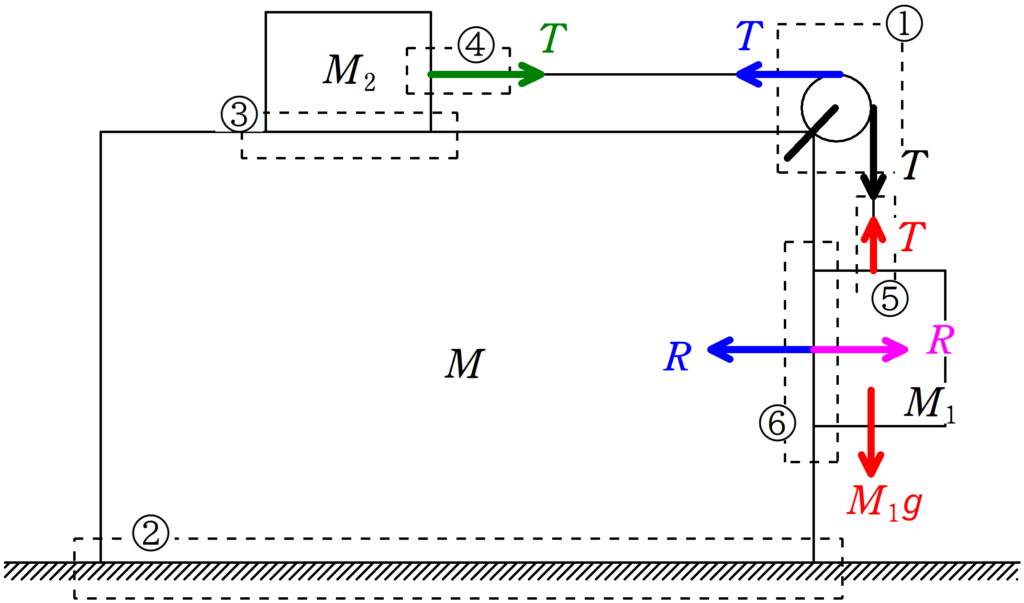
★ ①部分について
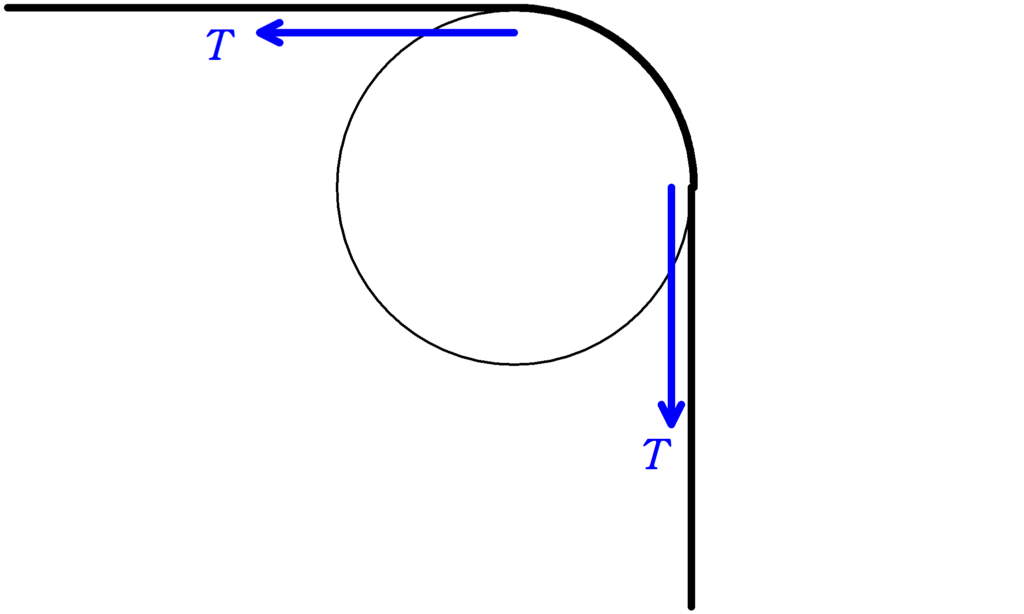

滑車は質量$M$の物体の一部と考えれば,上図のような張力がはたらきます.
★ ②と③部分について

垂直抗力ははたらきますが,摩擦力がはたらかないので力を図示していません.
★ ④と⑤部分について

張力がはたらきます.
★ ⑥部分について

質量$M$の物体と質量$M_{1}$の物体に垂直抗力がはたらきます.
とりあえず,上図の向きに$R$と設定します.
この2つの$R$は作用反作用の関係にあります.

それでは,質量$M$の物体の運動方程式から立てていきましょう.
水平面で静止している人からみた加速度を$A$(右向きを正)とすると,運動方程式は次のようになります.
★ 水平面からみた質量$M$の物体の運動方程式
$MA=-R-T$ $\dots (\ast)$
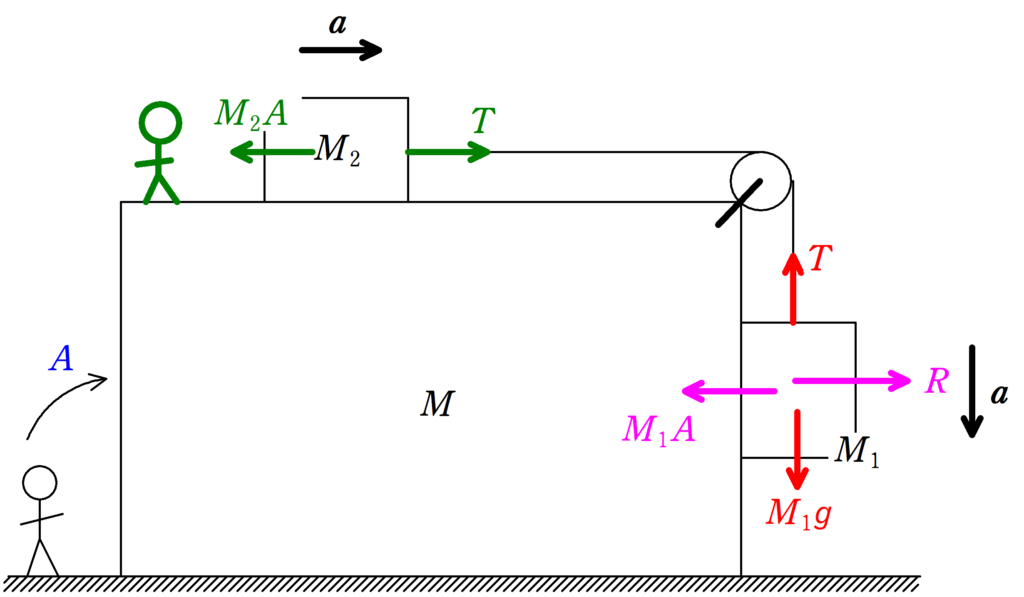

次に質量$M$の物体の上からみた質量$M_{1}$,$M_{2}$の運動方程式を立てます.
上図の緑色の観測者が加速度$A$で運動しているので,質量$M_{1}$と$M_{2}$には,加速度$A$の方向と反対方向に慣性力がはたらきます.
慣性力の大きさ$F$は
$F=(慣性力がはたらく物体の質量)×(観測者の加速度の大きさ)$
です.
質量$M$の物体の上で静止している観測者からみた質量$M_{2}$の物体の水平方向の加速度を$a$,おなじく,質量$M_{1}$の物体の鉛直下向きの加速度を$a$とします.
ちなみに,質量$M$の物体の上からみると,質量$M_{1}$は水平方向には動いていません.なので,つり合いの式を立てます.
★ 質量$M$の物体からみた$M_{1}$の水平方向のつり合いの式
$R=M_{1}A$ $\dots (2\ast)$
★ 質量$M$の物体からみた$M_{1}$の鉛直方向の運動方程式
$M_{1}a=M_{1}g-T$ $\dots (3\ast)$
★ 質量$M$の物体からみた$M_{2}$の水平方向の運動方程式
$M_{2}a=T-M_{2}A$ $\dots (4\ast)$

$(\ast)$~$(4\ast)$を解いて,$A$,$a$,$T$,$R$を求めましょう.
$M$$A$$=-$$R$$-$$T$ $\dots (\ast)$
$R$$=M_{1}$$A$ $\dots (2\ast)$
$M_{1}$$a$$=M_{1}g-$$T$ $\dots (3\ast)$
$M_{2}$$a$$=$$T$$-M_{2}$$A$ $\dots (4\ast)$
$(\ast)$と$(2\ast)$より$R$を消去する.
$M$$A$$=-M_{1}$$A$$-$$T$
$\therefore$ $T$$=-(M_{1}+M)$$A$ $\dots (5\ast)$
$(5\ast)$を$(3\ast)$と$(4\ast)$に代入して$T$を消去する.
$(3\ast)$:$M_{1}$$a$$=M_{1}g+(M_{1}+M)$$A$
$\therefore$ $a$$=g+\dfrac{M_{1}+M}{M_{1}}$$A$ $\dots$ $(6\ast)$
$(4\ast)$:$M_{2}$$a$$=-(M_{1}+M+M_{2})$$A$ $\dots$ $(7\ast)$
$(6\ast)$と$(7\ast)$より$a$を消去する.
$M_{2}(g+\dfrac{M_{1}+M}{M_{1}}$$A$$)=-(M_{1}+M+M_{2})$$A$
$\therefore$ $(M_{1}+M+M_{2}+\dfrac{M_{2}(M_{1}+M)}{M_{1}})$$A$$=-M_{2}g$
左辺をもう少し整理して$A$を求めましょう.
$\dfrac{(M_{1}+M_{2})(M_{1}+M)+M_{1}M_{2}}{M_{1}}$$A$$=-M_{2}g$
$A$$=-\dfrac{M_{1}M_{2}}{(M_{1}+M_{2})(M_{1}+M)+M_{1}M_{2}}g$ $\dots (8\ast)$
$(8\ast)$を$(7\ast)$を代入して
$a$$=\dfrac{M_{1}(M_{1}+M_{2}+M)}{(M_{1}+M_{2})(M_{1}+M)+M_{1}M_{2}}g$ $\dots (9\ast)$
$(8\ast)$を$(2\ast)$に代入して
$R$$=-\dfrac{M_{1}^{2}M_{2}}{(M_{1}+M_{2})(M_{1}+M)+M_{1}M_{2}}g$ $\dots (10\ast)$

$(10\ast)$から$R<0$であることが確認できるね.
つまり,設定した$R$の向きとは逆ということだね.
$(8\ast)$を$(5\ast)$に代入して
$T$$=\dfrac{M_{1}M_{2}(M_{1}+M)}{(M_{1}+M_{2})(M_{1}+M)+M_{1}M_{2}}g$ $\dots (11\ast)$

さて,質量$M$の物体からみると,質量$M_{1}$の物体が加速度$a$で等加速度運動をしています.
質量$M_{1}$の物体が加速度$a$で距離$h$だけ進むのにかかる時間を$\tau$とします.
等加速度運動の式より
$h=\dfrac{1}{2}a\tau^{2}$
$\tau^{2}=\dfrac{2h}{a}$ $\dots (12\ast)$
となります.
この時間の間に質量$M$の物体が移動する距離$x$は,加速度の大きさが$|A|$であるから,等加速度運動の式より
$\eqalign{x&=\dfrac{1}{2}|A|\tau^{2}\\&=\dfrac{1}{2}|A|\cdot \dfrac{2h}{a}\\&=\dfrac{h|A|}{a}\\&=\dfrac{M_{2}}{M_{1}+M_{2}+M}h}$
以上より,求める距離は
$x=\dfrac{M_{2}}{M_{1}+M_{2}+M}h$

コメント
[…] [有名問題]3つの物体の運動[東工大] 解法1NEKO今回は,東工大の有名問題を… 問題 […]