入試物理における$pV$図の利用の仕方 | Physicmath（フィジクマス）

$pV$図は熱力学の問題を解く際にとても役に立ちます．

$pV$図についての設問がなくとも，普段から$pV$図をかくことをおすすめします．

理由は次の4つです．

　状態の変化を意識しながら問題を解くことができる．

　たとえば，状態Aから状態Bまでは定圧変化．状態Bから状態Cまでは定積変化というように，状態の変化を確認する癖がつき，わけもわからず公式をつかって間違えてしまった・・・．なんてことが少なくなります．

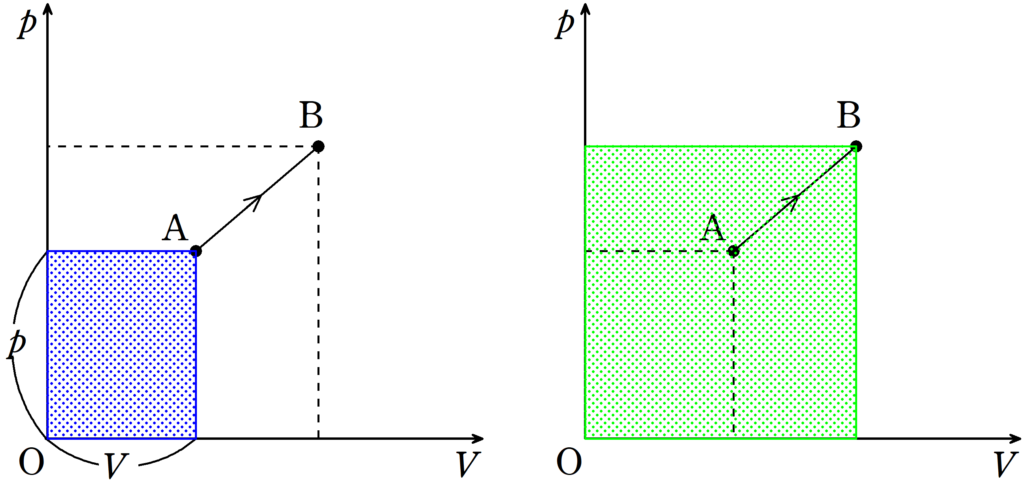
　理想気体の状態方程式は，圧力を$p$，体積を$V$，絶対温度を$T$，物質量を　

　 $n$，気体定数を$R$とすると，

$pV=nRT$

　この式を変形して

$T=\dfrac{pV}{nR}$

　$nR$は変化しないことが多く（そもそも$n$が変化してしまうと$pV$グラフはかけ

　ない），結局

絶対温度は圧力×体積に比例する

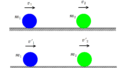
　となります．たとえば，上図でいえば，状態Aの絶対温度は青色の長方形の面積

　に比例し，状態Bでの絶対温度は緑色の長方形の面積に比例します．

　だから，計算しなくても見た目で

状態Aの絶対温度$<$状態Bの絶対温度

　であることがわかるのです．

　このように，見た目で絶対温度の変化が見えるのが$pV$グラフを用いるメリットの一つなのです．

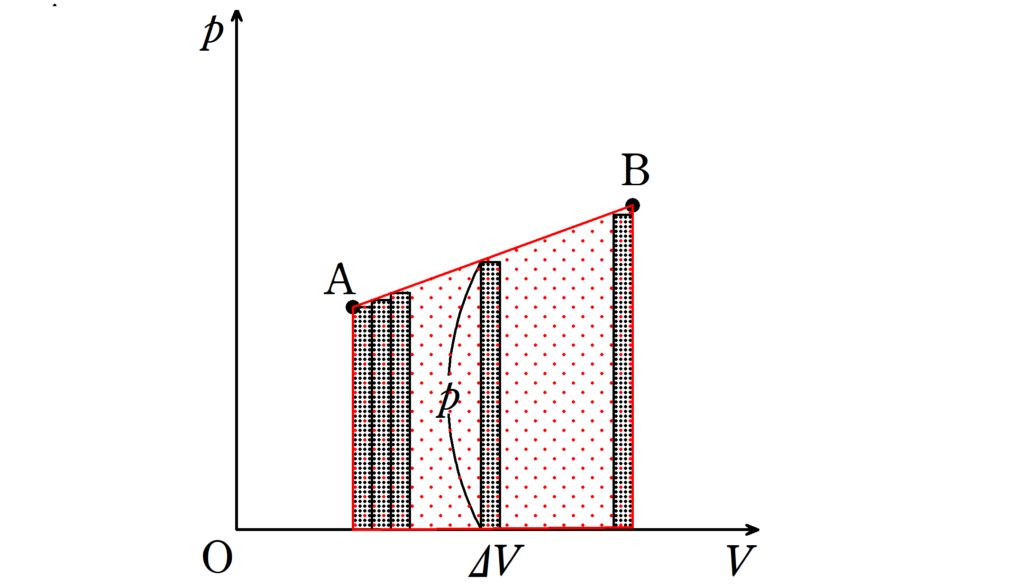
　上図のように，状態Aから状態Bに変化したときに気体がした仕事の絶対値は

曲線（直線）と$V$軸で囲まれた面積

　です．これは，面積を求める際に細かく長方形に分割していくと，長方形の面積は

$p \Delta V$

　となっていて，$\Delta V$だけ体積が変化したときにした仕事を表していることから

　確認できます．ここで注意点！

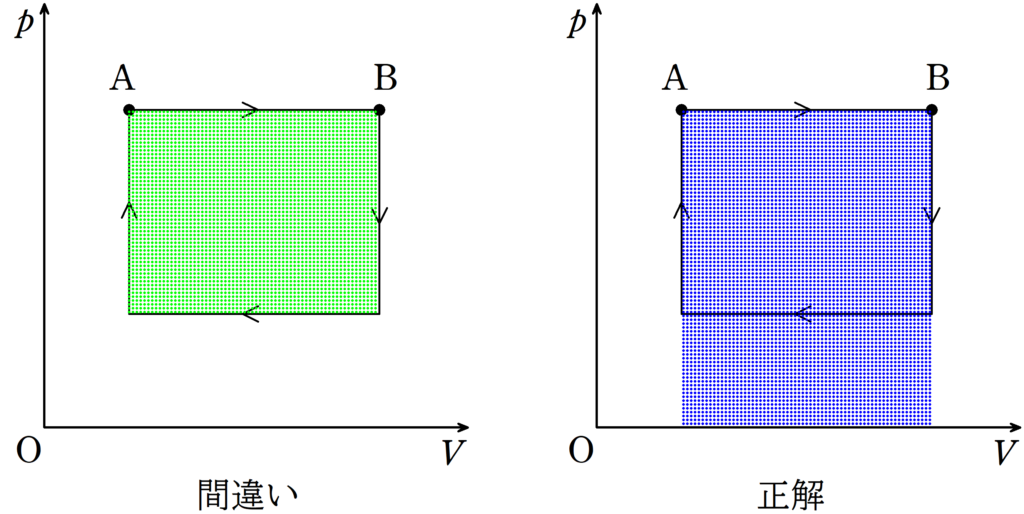
　状態Aから状態Bまでの仕事の計算を上図に左側，つまり，緑色部分の面積を求める人がいますが，正しくは右側の青色部分の面積を求めてください．

　なぜ$pV$図のグラフの面積が気体がした仕事の絶対値を表すのかがわかっていれば間違わないはずなのですが，”意味はわからないけど，とりあえず覚えておこう”という人は要注意です．

　熱力学の問題は状態の変化の数がたくさんあって，情報が複雑になりがちです．

　問題を確実に解き，解くスピードを上げるためには，”情報を整理”しながら解く必要があります．

　そこで，情報の整理に最適なのが，$pV$ 図．状態の圧力と体積を記入し，絶対温度も視覚的にわかる．また，その状態の変化の仕方もわかることが多いです．

最初は面倒かもしれませんが，後々のことを考えると，$pV$図をかいて，情報を整理する癖をつけた方がよいかと思います．

以上が$pV$図をかくメリットです．熱力学の問題は他分野に比べて短時間で得意分野にできると思います．たとえ，複雑な問題でも $pV$ 図利用して上手に問題を解いていきましょう．