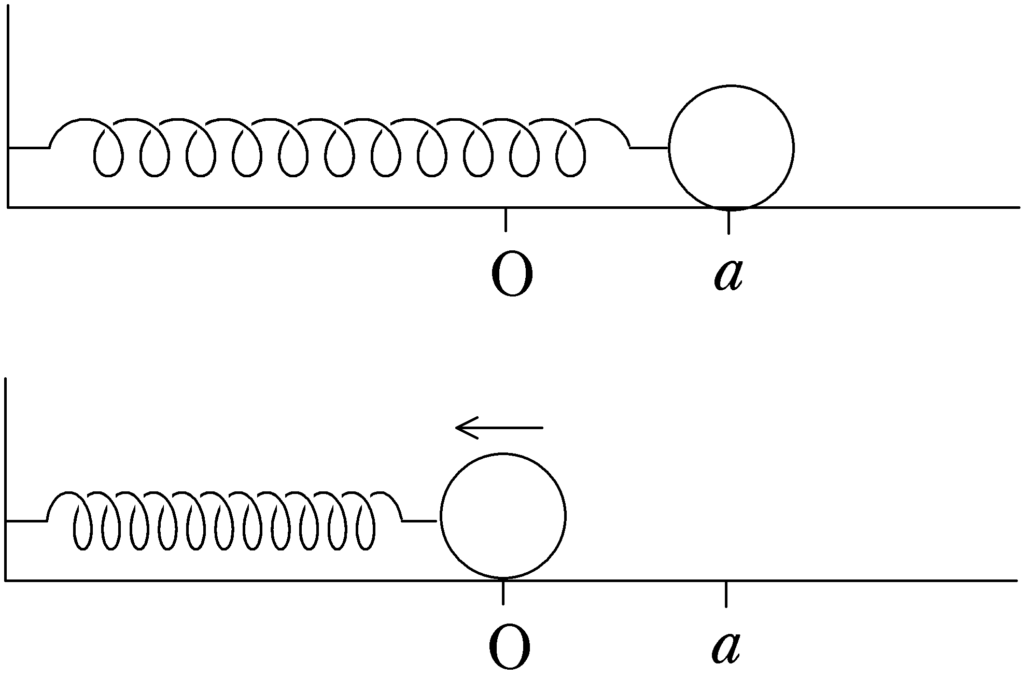
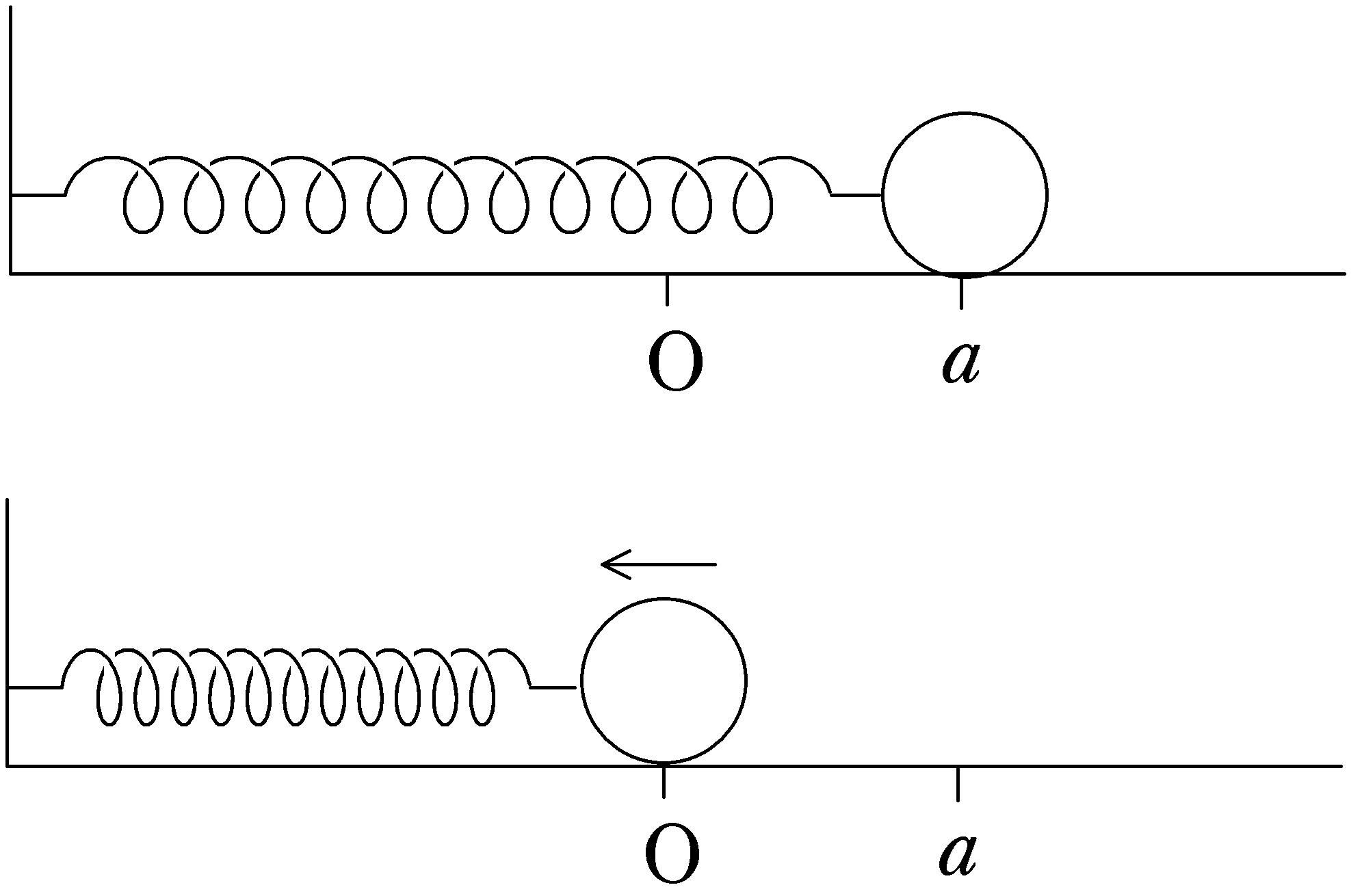
図のように，ばね定数$k$のばねの一端を壁に固定し，他端を質量$m$の物体にとりつけた．ばねが自然長になる位置を原点Oとし，ばねが伸びる方向に$x$軸をとる．
物体に力を加えて，$x=a$$(a>0)$まで移動させたのちに手を放すと物体は動き始めた．物体がはじめて自然長になるまでにばねがする仕事$W$を求めよ．
弾性力について確認しましょう．
ばね定数を$k$とする．
ばねの伸び，または縮みが$A$$(A>0)$であるとき，弾性力の大きさ$F$は
$F=kA$
弾性力の向きは，自然長に戻ろうとする向き．
はじめにはたらく力が$ka$で，移動距離が$a$だね．仕事が力×距離だから，
$ka\times a=ka^{2}$
かな．
いえ，それは間違いです．
弾性力は自然長に近づくほど小さくなるので，$a$だけ伸びているときにはたらく力で変化しないと考えてはいけません．
正確には，積分計算（または縦軸を力，横軸をばねの伸びとしたときのグラフの面積．）をする必要がありますが，やや面倒なので次の式を使いましょう．
保存力がする仕事を$W$，位置エネルギー変化を$\varDelta U$とすると，次の式が成り立つ．
$\varDelta U=-W$
たとえば，重力が正の仕事をしたら（鉛直下向きに移動），その分だけ位置エネルギーは減ってしまうし，重力が負の仕事をしたら（鉛直上向きに移動），その分位置エネルギーが増加するということだね．
はい．これを利用して問題を解きましょう．
はじめの弾性力による位置エネルギーが
$\dfrac{1}{2}ka^{2}$で，自然長に戻ったときの位置エネルギーが$0$なので，位置エネルギー変化$\varDelta U$は
$\varDelta U=0-\dfrac{1}{2}ka^{2}=-\dfrac{1}{2}ka^{2}$
です．なので，弾性力がした仕事$W$は
$W=-\varDelta U=\dfrac{1}{2}ka^{2}$(答)
となります．
他の保存力がする仕事の問題として頻出なのが，「万有引力がする仕事」です．よかったらこちらも参考に読んでみてください．
コメント