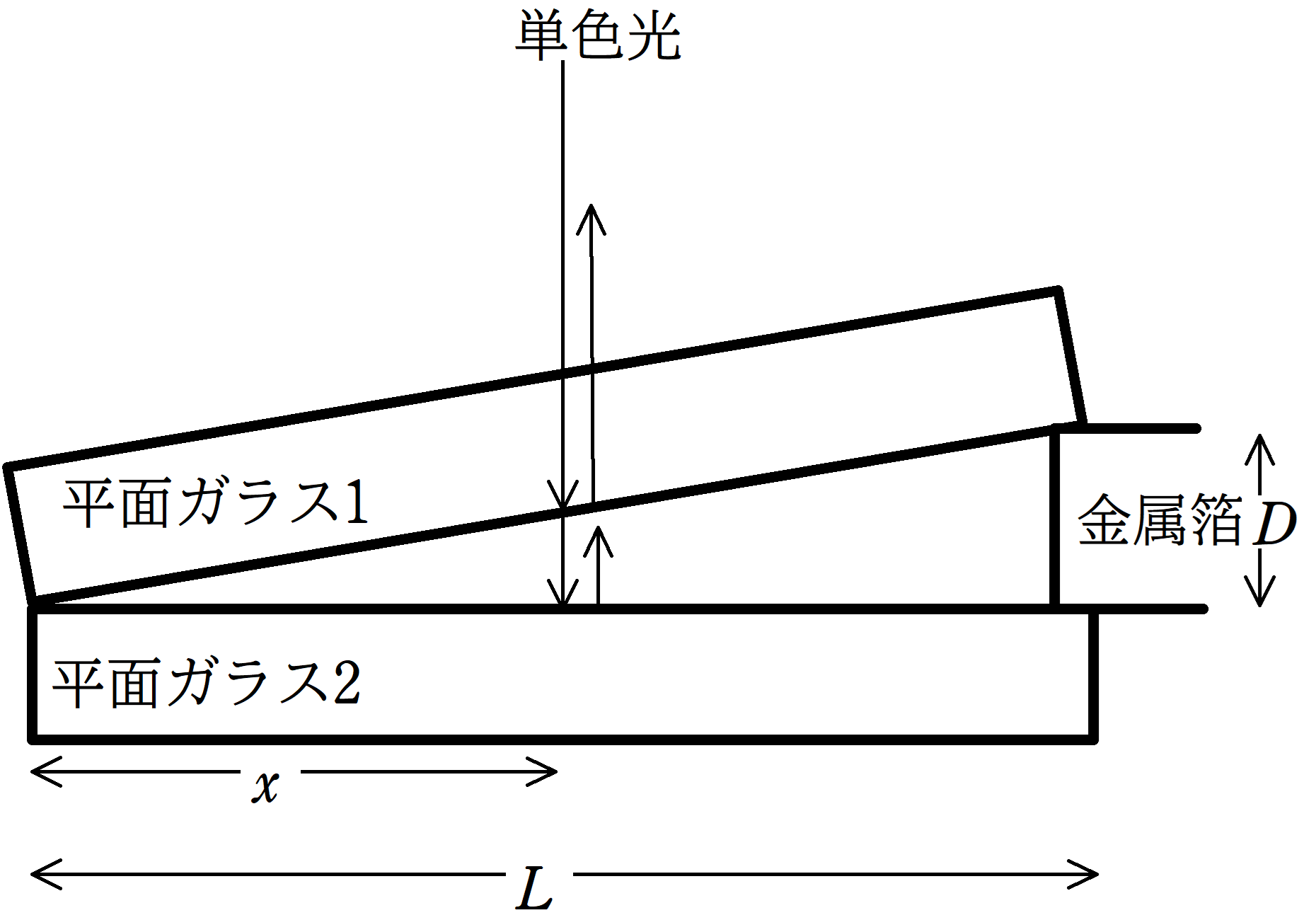
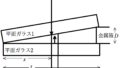
図のように空気に対する相対屈折率$n$の平板ガラス2を水平面に固定し,平面ガラス1を薄い金属箔ではさんで傾けておく.2枚のガラスが接する位置から金属箔までの距離を$L$,金属箔の厚さを$D$とする.鉛直上方から入射した光が同じ方向に反射される光を水平なスクリーンにあてて観測する.また,$D$が非常に小さいため,鉛直下向きに入射した光が反射される方向は鉛直上向きであるとしてよい.このとき,次の問いに答えよ.ただし,空気中での光の波長を$\lambda$とする.
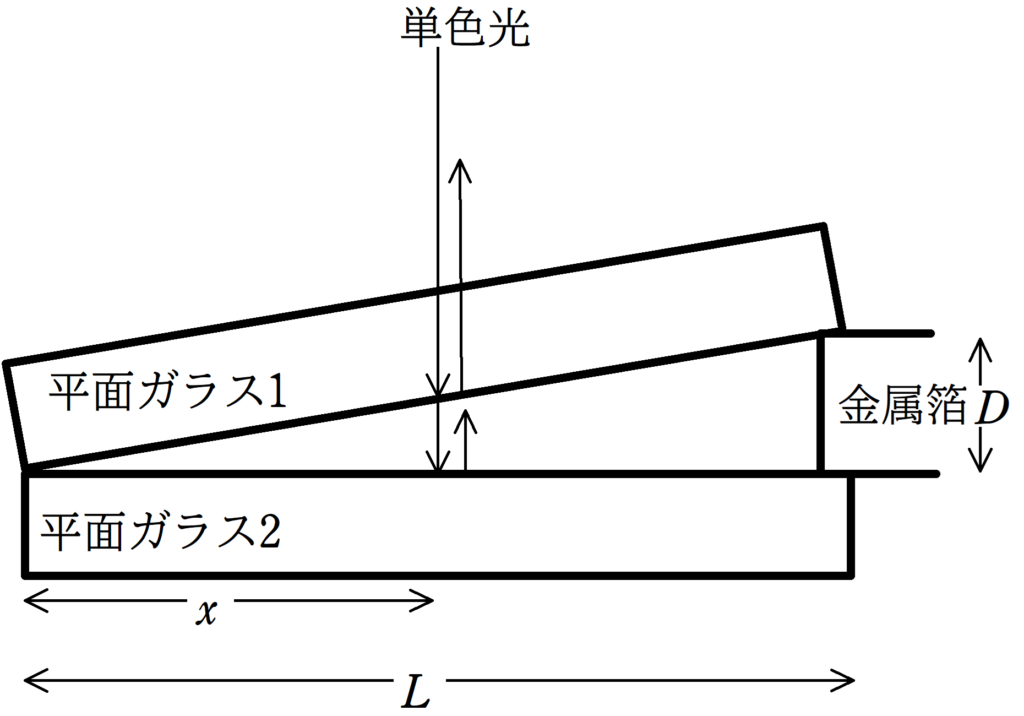
(1) 平面ガラス1,2の接触部分より水平に距離$x$の場所に入射する光について考える.鉛直上方から入射した単色光の一方は平面ガラス1下部で反射され,他方は平面ガラス2の上面で反射された.これらの光がスクリーンで干渉する際の位相差$\varDelta \varphi$を$L$,$x$,$D$,$\lambda$を用いて表せ.
(2) (1)のとき,強め合いの条件と弱め合いの条件を$L$,$x$,$D$,$\lambda$,自然数$m$を用いて表せ.
(3) スクリーンにおける明線の間隔$\varDelta x$を$L$,$D$,$\lambda$を用いて表せ.
<解答>
(1)

位相差については,次のことを確認しましょう.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
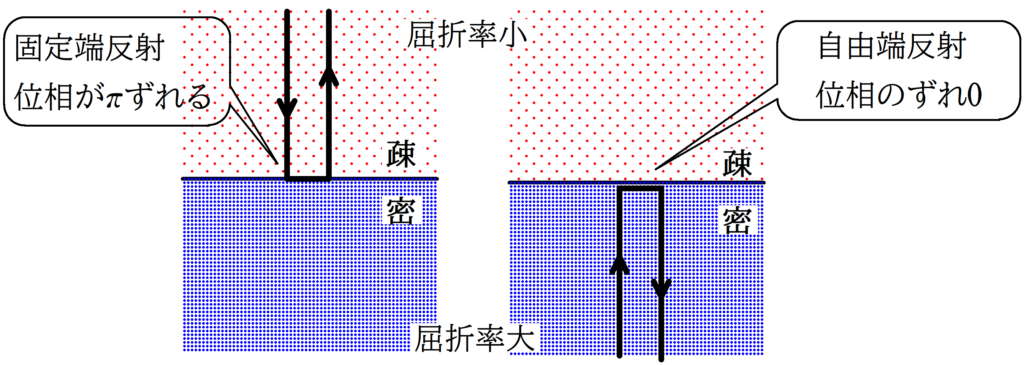
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$

また,固定端反射なのか自由端反射なのかは次の図で確認していきましょう.

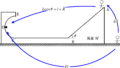
平面ガラス1,2のなす角を$\theta$とすると,$\tan\theta=\dfrac{D}{L}$です.すると,$x$における経路差は
$2x\tan\theta=\dfrac{2D}{L}x$
となります.
また,平面ガラス1下部における反射は自由端反射,平面ガラス2上部における反射は固定端反射なので,位相差$\varDelta \varphi$は
★ 位相差
$\varDelta \varphi=\dfrac{2\pi}{\lambda}\cdot \dfrac{2D}{L}x+\pi=\dfrac{4\pi D}{L\lambda}x+\pi$ (答)
(2)
★ 強め合いの条件
$\dfrac{4\pi D}{L\lambda}x+\pi=2\pi m$\\
$\dfrac{4\pi D}{L\lambda}x=(2m-1)\pi$ (答)
★ 弱め合いの条件
$\dfrac{4\pi D}{L\lambda}x+\pi=(2m-1)\pi$
$\dfrac{4\pi D}{L\lambda}x=(2m-2)\pi$ (答)
(3)

(2)の強め合いの条件より
$x=\dfrac{L\lambda}{2D}m-\dfrac{L\lambda}{4D}$
であり,これは公差が$\dfrac{L\lambda}{2D}$の等差数列になっています.
したがって,明線の間隔は$\varDelta x=\dfrac{L\lambda}{2D}$(答)

ちなみに,弱め合いの条件に,$m=1$を代入すると$x=0$となります.
つまり,平面ガラス1と平面ガラス2の接点部分は暗くなっているはずです.

コメント
[…] […]