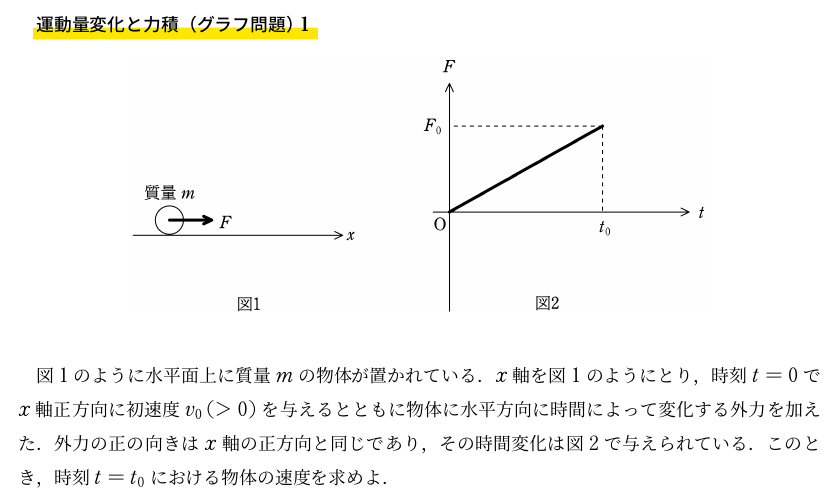
<問題>
<解答>
運動量変化と力積の関係を使って計算する.
力積は図2の$F-t$グラフから求める.そもそも力積とは(力)$\times $(時間)なので,$F-t$グラフと$t$軸で囲まれた面積が力積の大きさとなる.
運動量変化=力積
時間$\varDelta t$の間の速度の変化を$\varDelta \vec{v}$とする.質量を$m$とすると
$m\varDelta \vec{v}=$力積
の関係がある.
$t=t_{0}$と$F-t$グラフの直線と$t$軸で囲まれた面積は
$\dfrac{1}{2}F_{0}t_{0}$
なので,$t=0$から$t=t_{0}$までに物体に加えた力積の和は$\dfrac{1}{2}F_{0}t_{0}$となる.
時刻$t=t_{0}$における物体の速度を$v$とすると,運動量変化と力積の関係より
$mv-mv_{0}=\dfrac{1}{2}F_{0}t_{0}$
$\therefore\,\, v=v_{0}+\dfrac{F_{0}t_{0}}{2m}$(答)



コメント