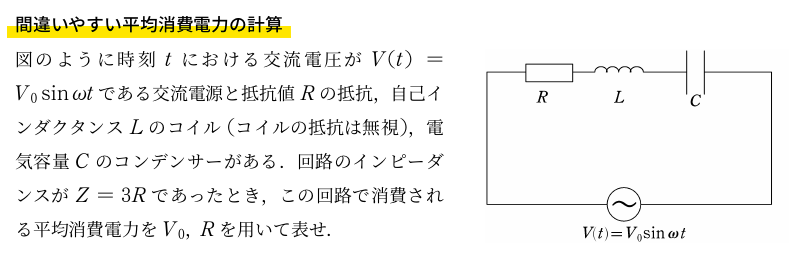
<問題>
<解答>
平均消費電力$P$を$P=\dfrac{1}{2}\dfrac{V_{0}^{2}}{Z}=\dfrac{V_{0}^{2}}{6R}$としないように注意.
インピーダンスが$3R$なので,回路に流れる電流の最大値を$i_{0}$とすると
$V_{0}=3Ri_{0}$ $\therefore\,\, i_{0}=\dfrac{V_{0}}{3R}$
がコイルとコンデンサーの平均消費電力は$0$なので,抵抗のみを考えて
$P=\dfrac{1}{2}Ri_{0}^{2}=\dfrac{1}{2}R\left(\dfrac{V_{0}}{3R}\right)^{2}=\dfrac{V_{0}^{2}}{18R}$(答)
※ ちなみに交流の基本問題演習はこちら
コンデンサーの平均消費電力が$0$である計算の例は下の記事で扱っています.
また,少し真面目に計算をすると,次のようになります.
回路に流れる電流を$i(t)=i_{0}\sin(\omega t+\delta)$(設定)とする.$\delta $は電圧からの位相のずれ.このとき,抵抗,コイル,コンデンサーにかかる電圧$V_{\rm R},V_{\rm L},V_{\rm C}$を計算する.
交流回路の計算では,電流が与えられたときに下記のことを使って,電圧を計算できる.
● 最大値について
回路素子にかかる電圧の最大値を$V_{0}$,流れる電流の最大値を$I_{0}$,リアクタンス(または抵抗)を$Z$とする.
このとき,次の関係が成り立つ.
$V_{0}=ZI_{0}$
$Z$は回路素子できまる.各周波数を$\omega$として
抵抗値$R$の抵抗のとき,$Z=R$
電気容量$C$のコンデンサーのとき,$Z=\dfrac{1}{\omega C}$
自己インダクタンス$L$のコイルのとき,$Z=\omega L$
● 位相のずれについて
1)電圧に対する電流の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$進む(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$遅れる(電圧が先に変化し,遅れて電流が変化する)
2)電流に対するで電圧の位相のずれ
抵抗:位相のずれはなし(オームの法則がいつでも成り立つ)
コンデンサー:$\dfrac{\pi}{2}$遅れる(電流が先に変化し,遅れて電荷が変化する)
コイル:$\dfrac{\pi}{2}$進む(電圧が先に変化し,遅れて電流が変化する)
$V_{\rm R}=Ri_{0}\sin(\omega t+\delta )$
$V_{\rm L}=\omega Li_{0}\sin\left(\omega t+\delta +\dfrac{\pi}{2}\right)=\omega Li_{0}\cos(\omega t+\delta)$
$V_{\rm C}=\dfrac{i_{0}}{\omega C}\sin\left(\omega t+\delta -\dfrac{\pi}{2}\right)=-\dfrac{i_{0}}{\omega C}\cos(\omega t+\delta)$
これらの電圧を足すと交流電源の電圧$V(t)$は
$\eqalign{V(t)&=V_{\rm R}+V_{\rm L}+V_{\rm C}\\&=Ri_{0}\sin(\omega t+\delta)+\omega Li_{0}\cos(\omega t+\delta)-\dfrac{i_{0}}{\omega C}\cos(\omega t+\delta)\\&=Ri_{0}\sin(\omega t+\delta)+\left(\omega L-\dfrac{1}{\omega C}\right)i_{0}\cos(\omega t+\delta)}$
したがって,時刻$t$における電力$P(t)$は
$\eqalign{P(t)&=V(t)i(t)\\&=\left\{Ri_{0}\sin(\omega t+\delta)+\left(\omega L-\dfrac{1}{\omega C}\right)i_{0}\cos(\omega t+\delta)\right\}\times i_{0}\sin(\omega t+\delta )\\&=Ri_{0}^{2}\sin^{2}(\omega t+\delta )+\left(\omega L-\dfrac{1}{\omega C}\right)i_{0}^{2}\sin(\omega t+\delta)\cos(\omega t+\delta)}$
したがって,平均消費電力$\overline{P(t)}$は
$\overline{P(t)}=Ri_{0}^{2}\overline{\sin^{2}(\omega t+\delta )}+\left(\omega L-\dfrac{1}{\omega C}\right)i_{0}^{2}\overline{\sin(\omega t+\delta)\cos(\omega t+\delta)}$
$\overline{\sin^{2}(\omega t+\delta )}=\overline{\cos^{2}(\omega t+\delta )}=\dfrac{1}{2}$,$\overline{\sin(\omega t+\delta)\cos(\omega t+\delta)}=0$なので,
$\overline{P(t)}=\dfrac{Ri_{0}^{2}}{2}$
インピーダンスが$3R$なので,回路に流れる電流の最大値を$i_{0}$とすると
$V_{0}=3Ri_{0}$ $\therefore\,\, i_{0}=\dfrac{V_{0}}{3R}$
したがって,
$\overline{P(t)}=\dfrac{1}{2}Ri_{0}^{2}=\dfrac{1}{2}R\left(\dfrac{V_{0}}{3R}\right)^{2}=\dfrac{V_{0}^{2}}{18R}$



コメント