
今回は面積速度一定の法則が成り立つ条件についての話です.
面積速度一定の法則が成り立つ条件は,誘導付きで2020年の東京大学の問題でも出題されました.
この記事では,入試によく出る面積速度一定の法則を使う出題例3つと,面積速度一定の法則が成り立つ条件の証明をします.
面積速度一定の法則とは

では,まず面積速度一定の法則をまとめましょう.
$\rm O$を中心として物体が運動しているときを考える.
物体の軌道面と平行な力が中心$\rm O$(または中心軸)を向くとき,面積速度$\dfrac{\Delta S}{\Delta t}$が一定となる.
面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である.
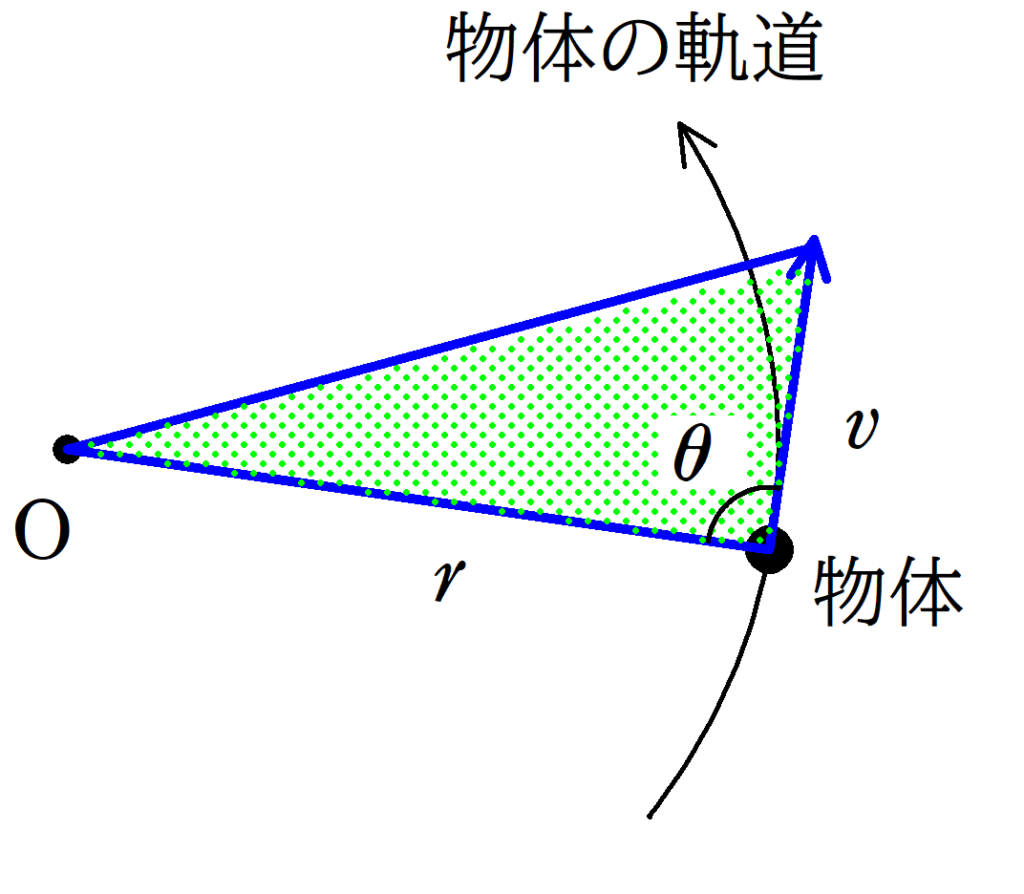
上図のように,$\rm O$と物体の距離が$r$,物体の速さを$v$,$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると,面積速度は
$\dfrac{\Delta S}{\Delta t}=\dfrac{1}{2}rv\sin\theta$

具体例はこちらです!
具体例1:太陽を周る地球の運動
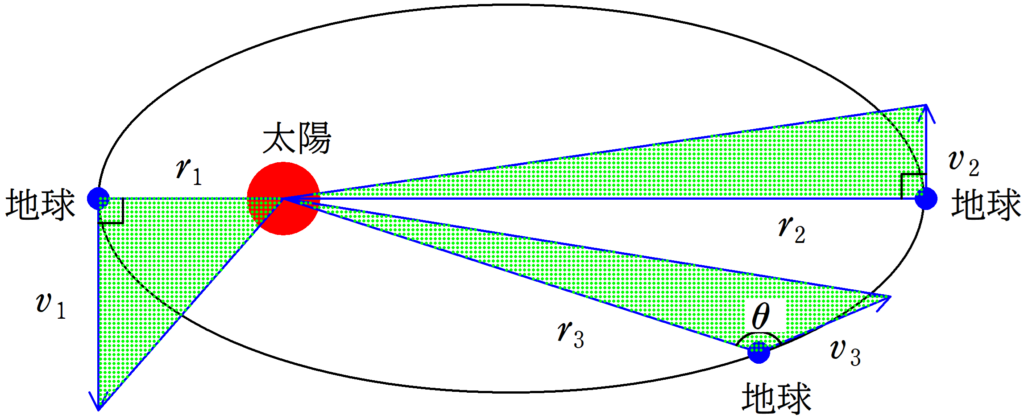

地球にはたらく力は万有引力のみです.
なので,面積速度一定の法則が成り立ちます.
$r_{1} , r_{2} , r_{3}$を太陽と地球との距離,$v_{1} , v_{2} , v_{3}$を地球の速さとします.
★ 面積速度一定の法則
$\dfrac{1}{2}r_{1}v_{1}=\dfrac{1}{2}r_{2}v_{2}=\dfrac{1}{2}r_{3}{v}_{3}\sin \theta$
具体例2:半径が変わる円運動
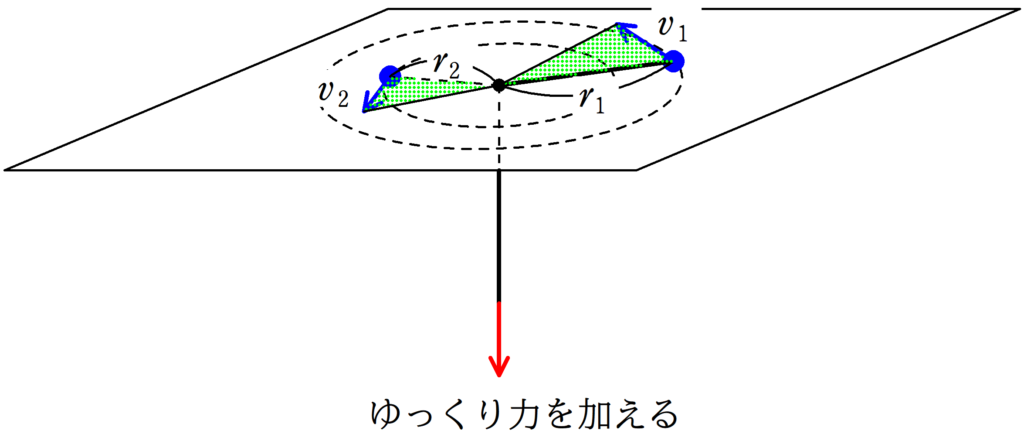

こちらは水平な台に穴をあけて,糸の一端を物体にとりつけ,他端に穴を通して円運動させる問題です.
同じ種類のものとして,2020年の早稲田大学-理工でも出題されました.
過去には東京大や京都大などでも出題されています.
半径$r_{1}$,速さ$v_{1}$で円運動している状態からひもにゆっくりと鉛直下向きに力を加えると,物体の軌道の半径は$r_{2}$,速さは$v_{2}$に変化したとします.
摩擦や空気抵抗,穴の大きさなどは無視をしましょう.

この問題では,物体にはたらくのが,張力だけで,中心向きにしか力がはたらいていないから面積速度が一定になるんだね.
★ 面積速度一定の法則
$\dfrac{1}{2}r_{1}v_{1}=\dfrac{1}{2}r_{2}v_{2}$
具体例3:円錐内の物体の運動
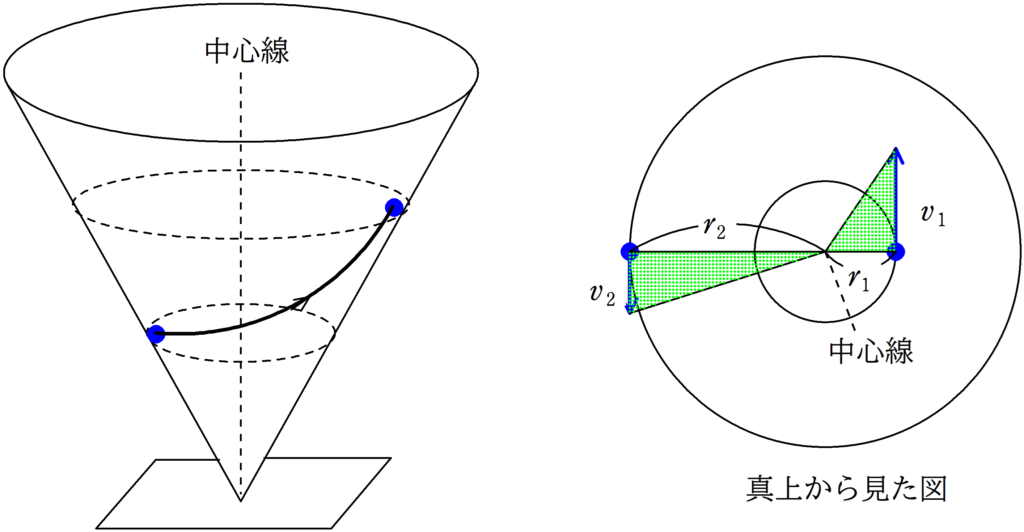

上図のように,円錐容器を逆さにして地面に固定します.
この際,中心線が水平面に対して垂直になるようにしておきましょう.
この円錐容器の中は空洞になっていて,物体をなめらかに運動させることができます.
円錐の内側に接するように物体をおき,ある大きさ以上の初速を与えると物体は上にあがりつつ曲線を描き,再び降下して帰ってきます.
最下点における水平面に平行な方向の速さを$v_{1}$,中心線からの距離を$r_{1}$,最高点における水平面に平行な方向の速さを$v_{2}$,中心線からの距離を$r_{2}$とすると,やはり面積速度が一定になります.

え!?
中心方向以外にも力がはたらいている気がするんだけど...
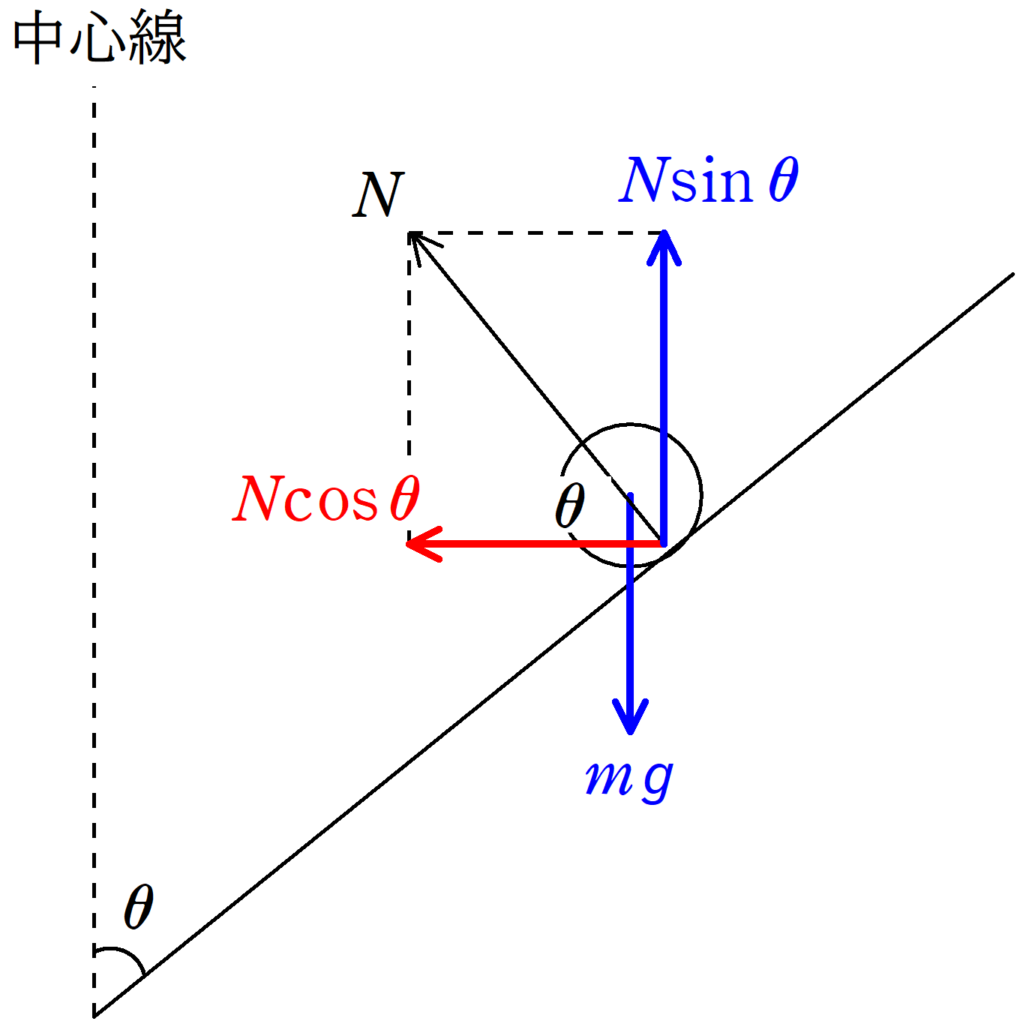

確かに鉛直方向に関しては垂直抗力と重力がかかりますが,上図の垂直抗力を分解した$N\cos\theta$は常に中心線を向いています.

つまり,水平面に平行な部分の面積速度が一定ってこと??

そういうことです.
なので,面積速度一定の法則を立てる際に,鉛直方向の速度成分を入れないように注意しましょう.
★ 面積速度一定の法則
$\dfrac{1}{2}r_{1}v_{1}=\dfrac{1}{2}r_{2}v_{2}$

この3つパターンは頭にいれておくといいね.
では,面積速度一定の法則を計算によって示しましょう!
面積速度一定の法則の証明
設定


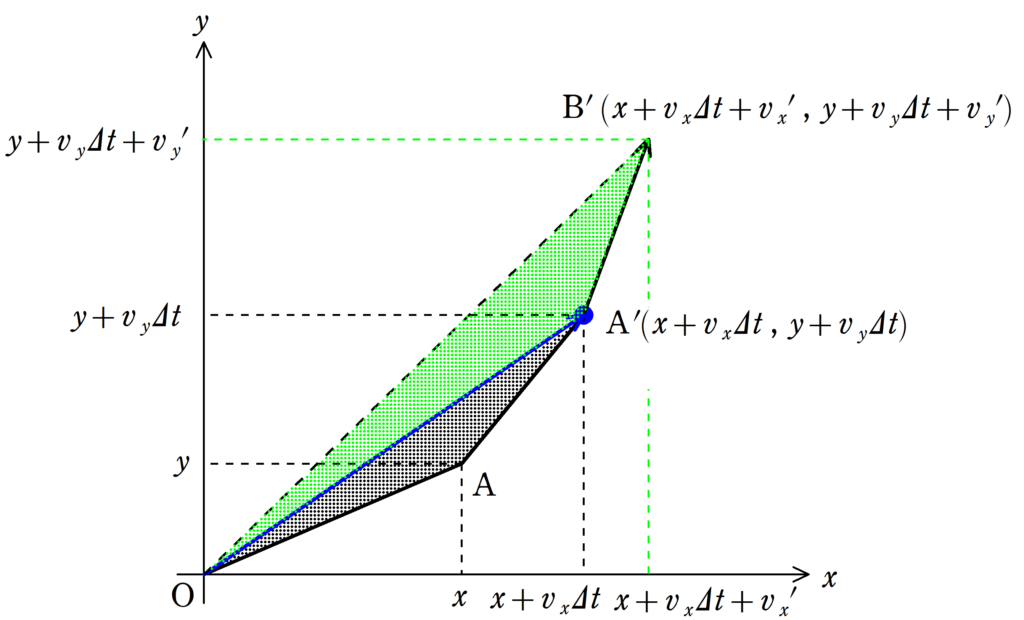
上図のように,ある時刻で物体が${\rm A} (x , y)$にいたとします.
このときの物体の速度ベクトルが$(v_{x} , v_{y})$です.
すると面積速度$V_{S}$は上図の緑色部分の面積となります.
${\rm O}(0 , 0)$,${\rm A} (x , y)$,${\rm B} (x+v_{x} , y+v_{y})$で囲まれた面積$V_{S}$はどのようになりますか?

数学で習った次の公式を使えばいいね!
${\rm O}(0 , 0)$,${\rm A}(a_{x} , a_{y})$,${\rm B}(b_{x} , b_{y})$で作られる三角形$\rm OAB$の面積$S$は
$S=\dfrac{1}{2}|a_{x}b_{y}-a_{y}b_{x}|$
三角形OABの面積$S$は
$S=\dfrac{1}{2}|\rm OA||\rm OB|\sin\angle \rm AOB$
です.上式を次のように変形していきます.
$\eqalign{S&=\dfrac{1}{2}\sqrt{|\rm OA|^{2}|\rm OB|^{2}\sin^{2}\angle \rm AOB}\cr&=\dfrac{1}{2}\sqrt{|\rm OA|^{2}|\rm OB|^{2}(1-\cos^{2}\angle \rm AOB)}\cr&=\dfrac{1}{2}\sqrt{|\rm OA|^{2}|\rm OB|^{2}-(|\rm OA||\rm OB|\cos\angle \rm AOB)^{2}}}$
$\overrightarrow{\rm OA}\cdot \overrightarrow{\rm OB}=|\rm OA||\rm OB|\cos\angle \rm AOB$より
$S=\dfrac{1}{2}\sqrt{{\rm OA^{2}}{\rm OB^{2}}-(\overrightarrow{\rm OA}\cdot \overrightarrow{\rm OB})^{2}}$ $\dots (\clubsuit)$
ところで,
${\rm OA^{2}}=a_{x}^{2}+a_{y}^{2}$,${\rm OB^{2}}=b_{x}^{2}+b_{y}^{2}$
より,
$\eqalign{{\rm OA^{2}}{\rm OB^{2}}&=(a_{x}^{2}+a_{y}^{2})(b_{x}^{2}+b_{y}^{2})\\&=a_{x}^{2}b_{x}^{2}+a_{x}^{2}b_{y}^{2}+a_{y}^{2}b_{x}^{2}+a_{y}^{2}b_{y}^{2}}$
$\eqalign{(\overrightarrow{\rm OA}\cdot \overrightarrow{\rm OB})^{2}&=(a_{x}b_{x}+a_{y}b_{y})^{2}\\&=a_{x}^{2}b_{x}^{2}+2a_{x}b_{x}a_{y}b_{y}+a_{y}^{2}b_{y}^{2}}$
これらを$(\clubsuit)$に代入して
$\eqalign{S&=\dfrac{1}{2}\sqrt{a_{x}^{2}b_{y}^{2}-2a_{x}a_{y}b_{x}b_{y}+a_{y}^{2}b_{x}^{2}}\\&=\dfrac{1}{2}\sqrt{(a_{x}b_{y}-a_{y}b_{x})^{2}}\\&=\dfrac{1}{2}|a_{x}b_{y}-a_{y}b_{x}|}$

上の公式を使って$\bigtriangleup \rm OAB$の面積$V_{S}$を求めよう.
$\eqalign{V_{S}&=\dfrac{1}{2}\{x(y+v_{y})-y(x+v_{x})\}\\&=\dfrac{1}{2}(xv_{y}-v_{x}y)}$ $\dots (\ast)$

これが面積速度です.
次に,物体に力がはたらいたときの面積速度の変化を考えましょう.
面積速度の変化

物体には常に力がはたらいています.
力がはたらくと,運動方程式
$ma=F$
からわかるように,加速度が生じます.
つまり,速度が変化するのです.
非常に短い時間$\Delta t$の間にもともと物体があった位置${\rm A}(x , y)$が${\rm A’}(x+v_{x}\Delta t , y+v_{y}\Delta t)$に移動したとしましょう.
※補足

$\Delta t$の間,速度$(v_{x} , v_{y})$は一定でいいの?力がはたらくから速度が変化するんじゃなかったっけ?

確かに,ここら辺は感覚的難しいところですね.
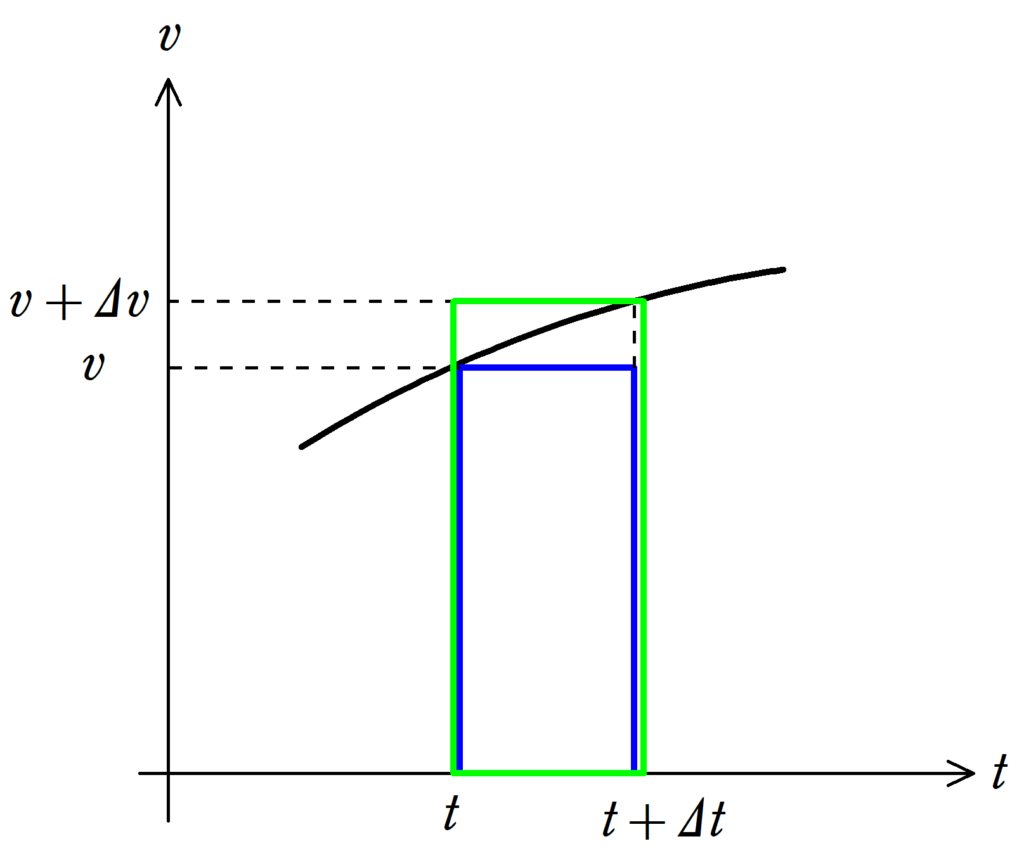

上図のような速度と時間のグラフ,いわゆる$v-t$グラフを考えてみましょう.
時刻$t$のときの速さが$v$(今回は$v>0 , \Delta v>0$と考えます.)で,$\Delta t$経った後の時刻$t+\Delta t$での速さを$v+\Delta v$とします.
仮に,一定の速さ$v$で$\Delta t$時間が経ったときに移動した距離はどうなりますか?

移動距離は$v\Delta t$だね!

しかし,実際は速さは変化しているので,正確な移動距離とは言えません.
そこで,少し大きく見積もってみます.
一定の速さ$v+\Delta v$で$\Delta t$時間が経ったときに移動した距離はどうなりますか?

移動距離は$(v+\Delta v)\Delta t$だね!

ここで,$\Delta t$は非常に小さいです.
すると,速度の変化$\Delta v$も小さくなります.
2つの小さいもの同士の掛け算は他のものに比べてさらに小さくなります.
つまり
$\Delta v \Delta t \approx 0$
としましょう.

すると
$\eqalign{(v+\Delta v)\Delta t&=v\Delta t+\Delta v\Delta t\\&\approx v\Delta t}$
になるから,大きく見積もっても結局$v\Delta t$と考えることができるんだね.
こういうのって物理の問題でたびたび見かけるよね・・・
短い時間$\Delta t$の間に,どちらが変化してどちらを一定にみなすを見極める目安はないの?

高校物理で出てくる式としては
$v=\dfrac{\Delta x}{\Delta t}$
$a=\dfrac{\Delta v}{\Delta t}$
$i=\dfrac{\Delta Q}{\Delta t}$
$力積=F\Delta t$
$\omega =\dfrac{\Delta \theta}{\Delta t}$
時間以外では微小な$\Delta x$について,次のものがあります.
$\Delta W=F\Delta x$
$E=-\dfrac{\Delta V}{\Delta x}$
これらの$\Delta$がついていない物理量が一定みなすものです.

そう考えると,$\Delta$を含めて公式を覚えておいた方がいいんだね.

さて,本題にもどりましょう.
物体の位置が,${\rm A’}(x+v_{x}\Delta t , y+v_{y}\Delta t)$のときの速度を$(v_{x}’, v_{y}’)$とします.
このときの面積速度$S_{V}’$を計算しましょう.
ここでも$\Delta $どうしの積は無視します.
$\rm O (0,0)$,${\rm A’}(x+v_{x}\Delta t , y+v_{y}\Delta t)$,${\rm B’}(x+v_{x}\Delta t+v_{x}’ , y+v_{y}\Delta t+v_{y}’)$として,$S_{V}’$は$\bigtriangleup \rm OA’B’$の面積ですね.
$S_{V}’=\dfrac{1}{2}\{(x+v_{x}\Delta t)(y+v_{y}\Delta t+v_{y}’)-(y+v_{y}\Delta t)(x+v_{x}\Delta t+v_{x}’)\}$ $\dots (2\ast)$
について,
$\eqalign{&(x+v_{x}\Delta t)(y+v_{y}\Delta t+v_{y}’)\\&=xy+xv_{y}\Delta t+xv_{y}’+yv_{x}\Delta t+v_{x}v_{y}(\Delta t)^{2}+v_{x}v_{y}’\Delta t\\&\approx xy+xv_{y}\Delta t+xv_{y}’+yv_{x}\Delta t+v_{x}v_{y}’\Delta t}$ $\dots$ ①
と
$\eqalign{&(y+v_{y}\Delta t)(x+v_{x}\Delta t+v_{x}’)\\&=xy+yv_{x}\Delta t+yv_{x}’+xv_{y}\Delta t+v_{x}v_{y}(\Delta t)^{2}+v_{x}’v_{y}\Delta t\\&\approx xy+yv_{x}\Delta t+yv_{x}’+xv_{y}\Delta t+v_{x}’v_{y}\Delta t}$ $\dots$ ②
①-②を計算すると
①-②$=xv_{y}’-yv_{x}’+(v_{x}v_{y}’-v_{x}’v_{y})\Delta t$ $\dots ③$
さらに,物体の加速度を$(a_{x},a_{y})$とすると,加速度の定義より
$a_{x}=\dfrac{v_{x}’-v_{x}}{\Delta t}$ $\therefore$ $v_{x}’=v_{x}+a_{x}\Delta t$
$a_{y}=\dfrac{v_{y}’-v_{y}}{\Delta t}$ $\therefore$ $v_{y}’=v_{y}+a_{y}\Delta t$

今度は加速度を一定とみなして計算しているね.

はい.
これを③に代入しましょう.
やはり$(\Delta t)^{2}\approx 0$とします.
$\eqalign{&xv_{y}’-yv_{x}’+(v_{x}v_{y}’-v_{x}’v_{y})\Delta t\\&=x(v_{y}+a_{y}\Delta t)-y(v_{x}+a_{x}\Delta t)+\{v_{x}(v_{y}+a_{y}\Delta t)-(v_{x}+a_{x}\Delta t)v_{y}\}\Delta t\\ &= xv_{y}-yv_{x}+xa_{y}\Delta t-ya_{x}\Delta t+(v_{x}a_{y}-a_{x}v_{y})\cdot (\Delta t)^2\\&\approx xv_{y}-yv_{x}+xa_{y}\Delta t-ya_{x}\Delta t }$ $\dots$ ④
④を$(2\ast)$に代入して
$S_{V}’=\dfrac{1}{2}(xv_{y}-yv_{x})+\dfrac{1}{2}(xa_{y}-ya_{x})\Delta t$ $\dots (3\ast)$
$(\ast)$と$(3\ast)$より面積速度の変化$S_{V}’-S_{V}$は
$S_{V}’-S_{V}=\dfrac{1}{2}(xa_{y}-ya_{x})\Delta t$ $\dots (\heartsuit)$

$(\heartsuit)$より,面積速度が変化しない条件を考えます.

$xa_{y}-ya_{x}=0$になればいいね.
運動方程式
$ma_{x}=F_{x}$,$ma_{y}=F_{y}$
より
$a_{x}=\dfrac{F_{x}}{m}$,$a_{y}=\dfrac{F_{y}}{m}$
なので,条件は次のように書き直せるね.
$\eqalign{xa_{y}-ya_{x}&=0\cr x\cdot \dfrac{F_{y}}{m}-y\cdot \dfrac{F_{x}}{m}&=0 \cr xF_{y}-yF_{x}&=0}$

この式は力が原点を向くことを示しているね.
たとえば,$x\neq 0$,$F_{x}\neq 0$のときは
$\dfrac{F_{y}}{F_{x}}=\dfrac{y}{x}$
と変形できることからも確認できるね.

はい.
ということで,面積速度が時間によらず一定になる条件は
力が原点を向く
ときになります.
今回は原点を中心としましたが,結局常に同じ方向に力が向けば面積速度は一定になります.

ということで,面積速度一定の法則が成り立つことの証明でした.
最後に面積速度一定の法則についてのまとめをもう一度確認しておきましょう.
$\rm O$を中心として物体が運動しているときを考える.
物体の軌道面と平行な力が中心$\rm O$(または中心軸)を向くとき,面積速度$\dfrac{\Delta S}{\Delta t}$が一定となる.
面積速度は中心$\rm O$と物体を結ぶ線分が単位時間あたりに通過する面積である.

上図のように,$\rm O$と物体の距離が$r$,物体の速さを$v$,$\rm O$と物体を結ぶ線分と速度とのなす角を$\theta$とすると,面積速度は
$\dfrac{\Delta S}{\Delta t}=\dfrac{1}{2}rv\sin\theta$



コメント
[…] [面積速度一定の法則]入試に出る3つのパターン+証明[2020年の東大でも出題] […]
[…] [面積速度一定の法則]入試に出る3つのパターン+証明[2020年の東大でも出題]… […]
[…] [面積速度一定の法則]入試に出る3つのパターン+証明[2020年の東大でも出題]… 問題 […]
[…] [面積速度一定の法則]入試に出る3つのパターン+証明[2020年の東大でも出題]… 問題 […]