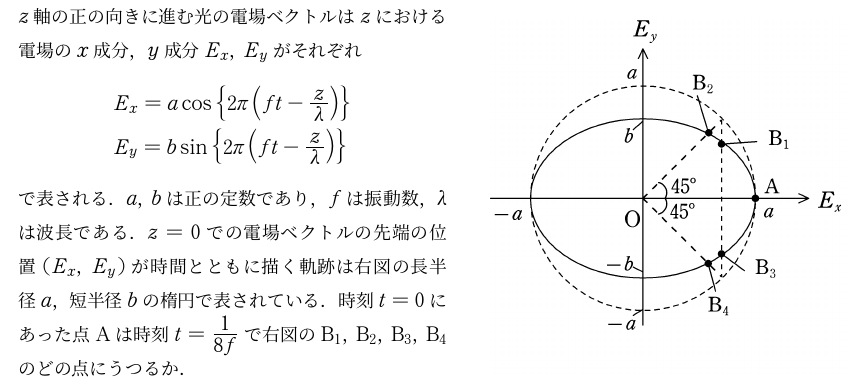
<問題>
<解答>
ほぼ数学の問題です.$z=0$において,$E_{x}=a\cos(2\pi ft)$,$E_{y}=b\sin(2\pi ft)$より,
$\dfrac{E_{x}}{a}=\cos(2\pi ft)$, $\dfrac{E_{y}}{b}=\sin(2\pi ft)$
であり,$\cos^{2}(2\pi ft)+\sin^{2}(2\pi ft)=1$を用いると
$\dfrac{E_{x}^{2}}{a^{2}}+\dfrac{E_{y}^{2}}{b^{2}}=1$
であり,楕円を描く.(これは問題の図にある)$t=\dfrac{1}{8f}$のとき,
$E_{x}=a\cos\left(2\pi \times \dfrac{1}{8f}\right)=a\cos\dfrac{\pi}{4}$
$E_{y}=b\sin\left(2\pi \times \dfrac{1}{8f}\right)=b\sin\dfrac{\pi}{4}$
より,$t=\dfrac{1}{8f}$のとき,第1象限にあるから,$\rm B_{1},B_{2}$のどちらかであることがわかる.
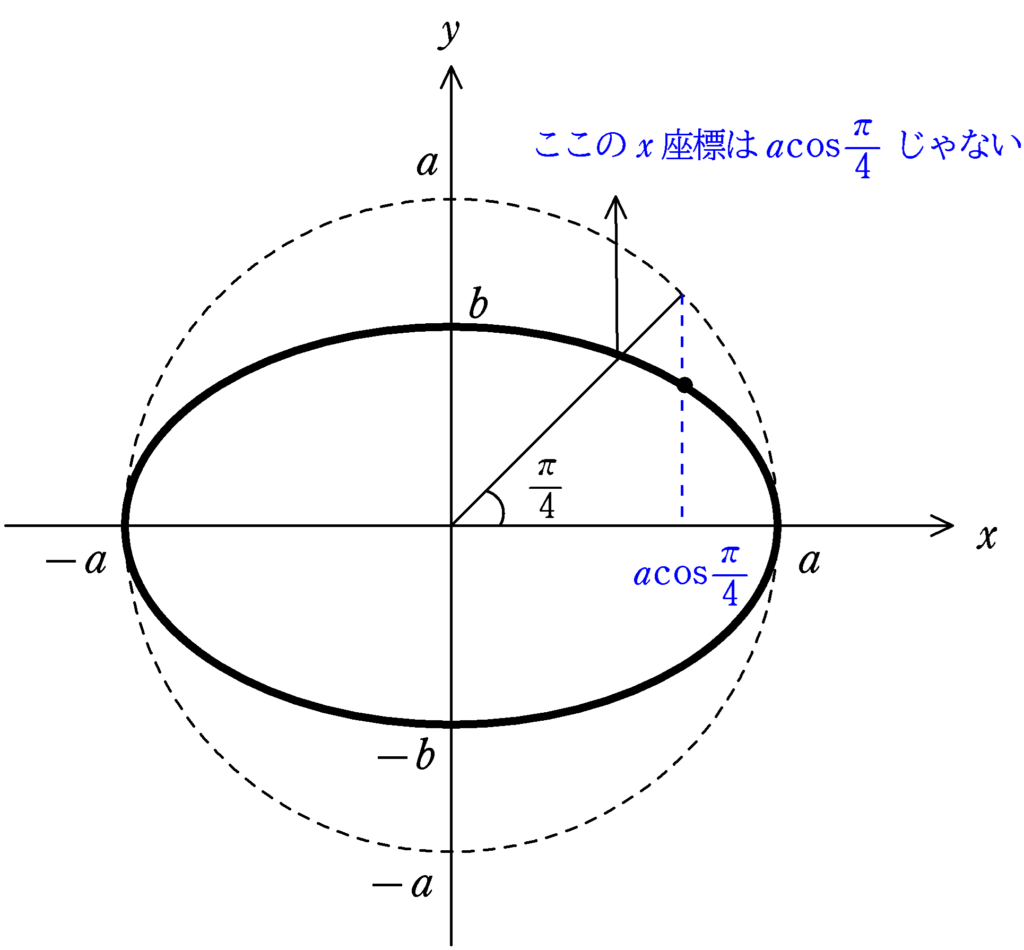
このとき,半径$a$の円を参考に$a\cos\dfrac{\pi}{4}$の位置を調べると上図のようになる.$E_{x}$座標が$a\cos\dfrac{\pi}{4}$で楕円上にある点を選べば,答えは点$\rm B_{1}$(答)
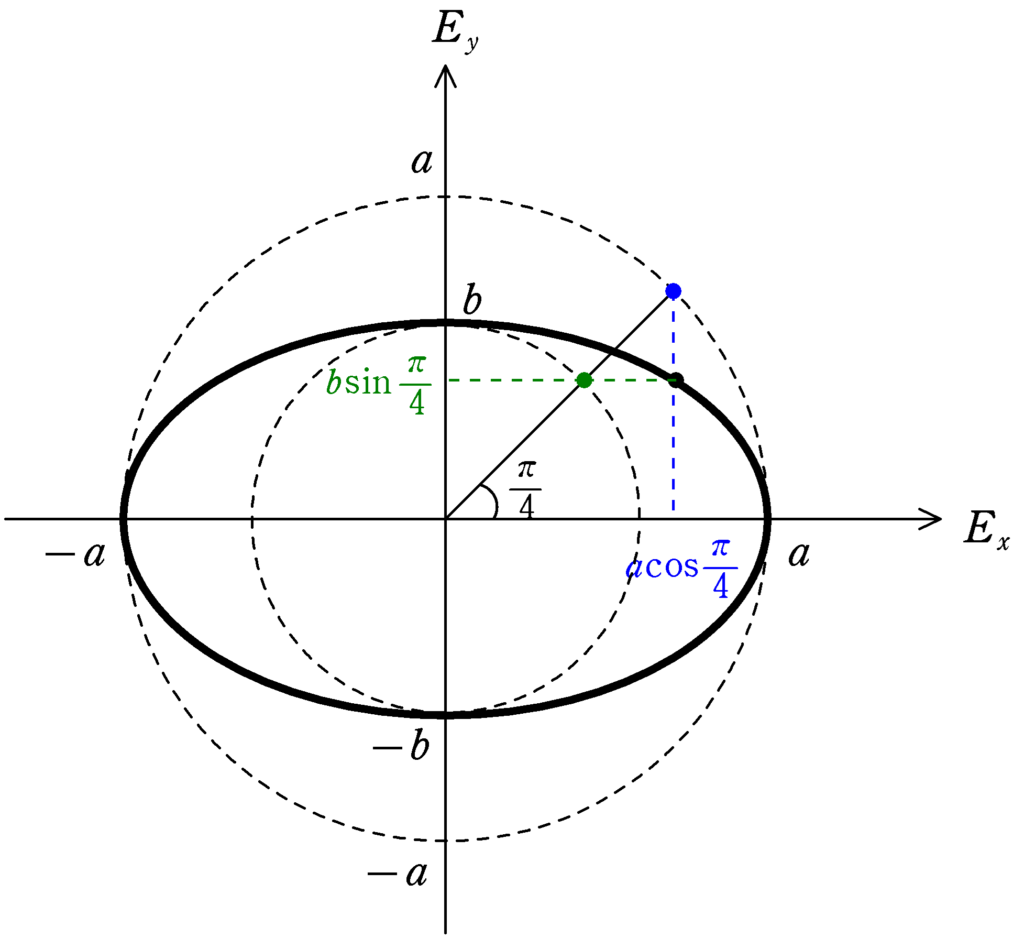
ちなみに,半径$b$の円から$E_{y}$座標$b\sin\dfrac{\pi}{4}$もわかる.



コメント