
今回は,エネルギーの原理の式
$\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}=W$
の式を導出します.
導出の過程で,仕事の計算の仕方のルールについて,確認しましょう.
質量$m$の物体の速さが$v_{0}$から$v$に変化したとき,この間に外力がした仕事を$W$とすると
$\dfrac{1}{2}mv^2-\dfrac{1}{2}mv_{0}^{2}=W$
の関係がある.

では,特殊なケースから順を追って話しましょう.
一次元の等加速度運動の場合

まずは,一次元の等加速度運動から考えます.
等加速度運動の式を確認しましょう.
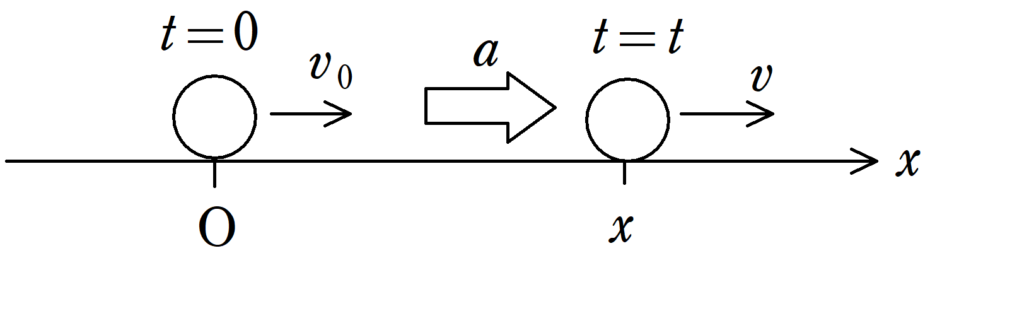
物体は加速度$a$で$x$軸上を運動している.$t=0$において,原点にある物体が,時刻$t$に座標$x$に移動した.初速度を$v_{0}$,時刻$t$における速度を$v$とするとき,次の関係式が成り立つ.
$v=v_{0}+at$ $\dots (\ast)$
$x=v_{0}t+\dfrac{1}{2}at^2$ $\dots (2\ast)$
$v^{2}-v_{0}^{2}=2ax$ $\dots (3\ast)$

このうち,$(3\ast)$を使います.
両辺に$\dfrac{1}{2}m$をかけてみましょう.
下では,$x$方向の加速度であることを強調するために,加速度$a$を$a_{x}$としました.
$v^{2}-v_{0}^{2}=2ax$の両辺に$\dfrac{1}{2}m$をかけて
$\eqalign{\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}&=\dfrac{1}{2}m\cdot 2a_{x}x\cr\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}&=ma_{x}x}$ $\dots (4\ast)$

さらに,$x$方向の物体の運動方程式を考えます.
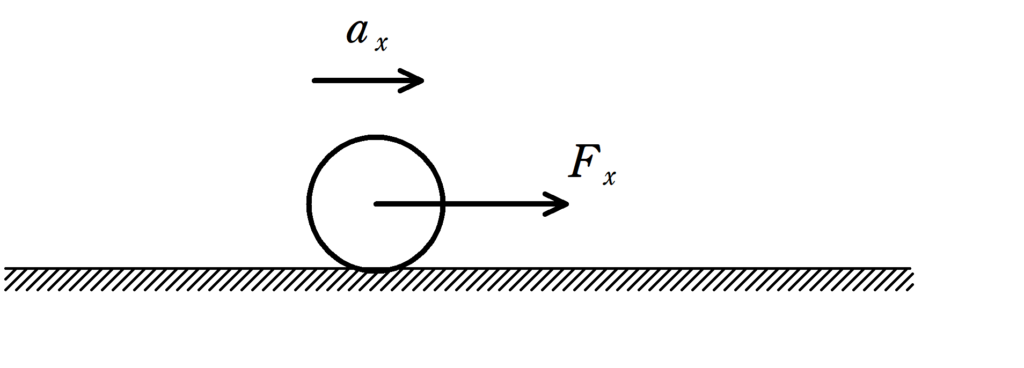
運動方程式は
$ma_{x}=F_{x}$ $\dots (5\ast)$

$(5\ast)$を$(4\ast)$に代入します.
$\eqalign{\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}&=ma_{x}x\\&=F_{x}x=W_{x}}$

$W_{x}=F_{x}x$が外力がした仕事です.

でもこれって,等加速度運動の式から導出したんだから,等加速度運動のときしか使えないんじゃないの??
一次元の非等加速度運動の場合

等加速度運動でないときは,等加速度運動とみなせるくらいに$\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^2=W$を分割します.
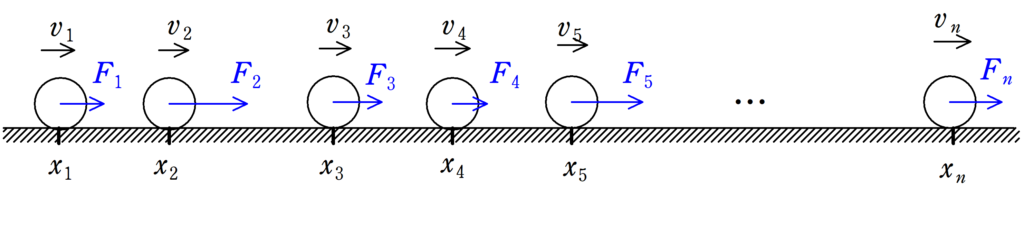
$\cancel{\dfrac{1}{2}mv_{2}^{2}}-\dfrac{1}{2}mv_{1}^{2}=F_{1}(x_{2}-x_{1})$
$\cancel{\dfrac{1}{2}mv_{3}^{2}}-\cancel{\dfrac{1}{2}mv_{2}^{2}}=F_{2}(x_{3}-x_{2})$
$\cancel{\dfrac{1}{2}mv_{4}^{2}}-\cancel{\dfrac{1}{2}mv_{3}^{2}}=F_{3}(x_{4}-x_{3})$
$\dots$
$\dfrac{1}{2}mv_{n}^{2}-\cancel{\dfrac{1}{2}mv_{n-1}^{2}}=F_{n-1}(x_{n}-x_{n-1})$

これらを全部足し合わせると,斜線部分は消えますね.
足し合わせたものをかくと,次のようになります.
下では
$W_{1}=F_{1}(x_{2}-x_{1}) ,W_{2}=F_{2}(x_{3}-x_{2}),\dots , F_{n-1}(x_{n}-x_{n-1})$
としました.
$\dfrac{1}{2}mv_{n}^{2}-\dfrac{1}{2}mv_{1}^{2}=W_{1}+W_{2}+\dots+W_{n-1}$

この式によれば,最後の運動エネルギーと最初の運動エネルギーの差が今までの仕事の和になっているね.

そういうことになります.
そして,その仕事の計算ですが,$W=F_{x}x$は$W=ma_{x}x$からきたので,$F_{x}$は$x$方向の力となります.

だから速度に対して垂直な力の向きの力は仕事が0なんだね!
仕事の正負について

仕事には,正の仕事と負の仕事があったよね?
どう区別するの?

物体にはたらく力の方向と物体の動く方向が同じ向きであれば正の仕事,逆向きであれば負の仕事です.
次の4つの場合を考えてみましょう.
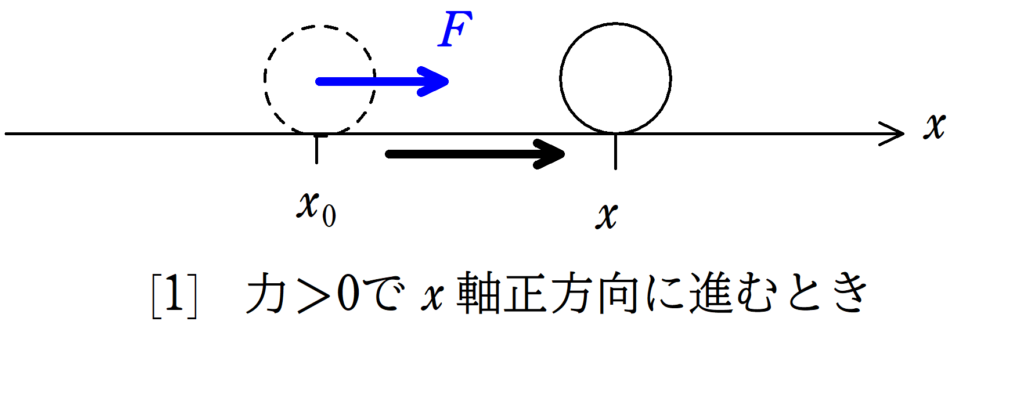

このとき,仕事は
$W=F(x-x_{0})$
で,$F$が正,$x-x_{0}$が正だから$F$は正だね.
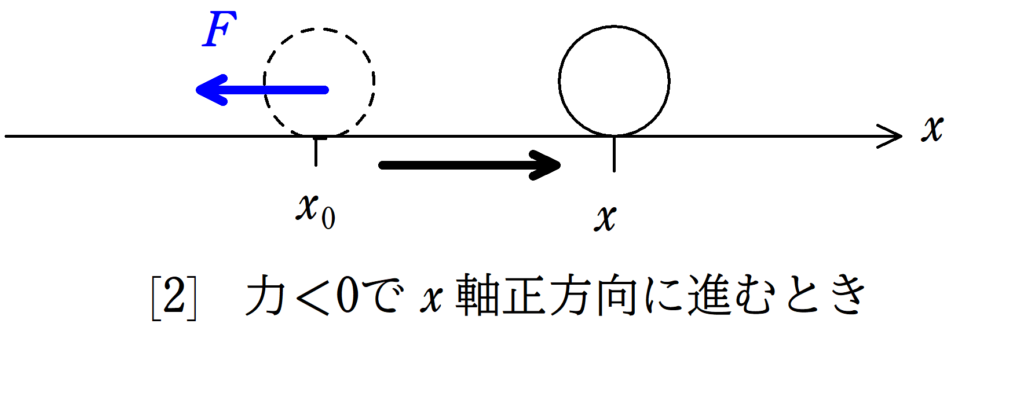

このとき,仕事は
$W=F(x-x_{0})$
で,$F$が負,$x-x_{0}$が正だから$F$は負だね.
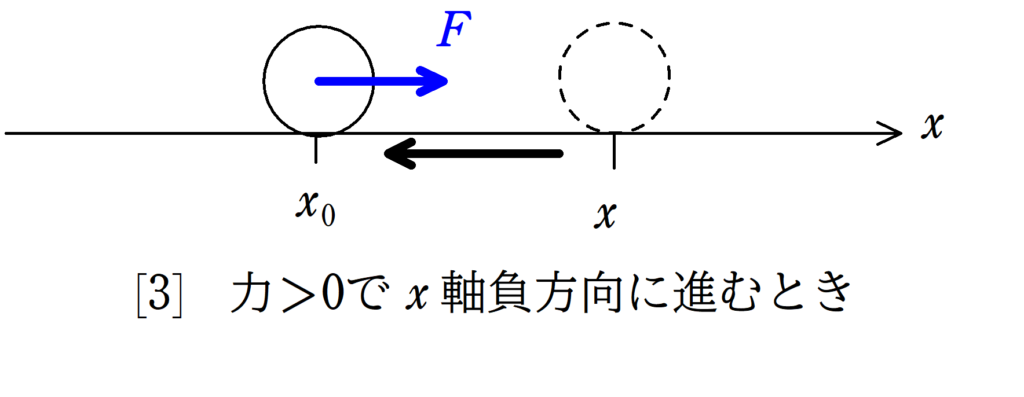

このとき,仕事は
$W=F(x_{0}-x)$
で,$F$が正,$x_{0}-x$が負だから$F$は負だね.
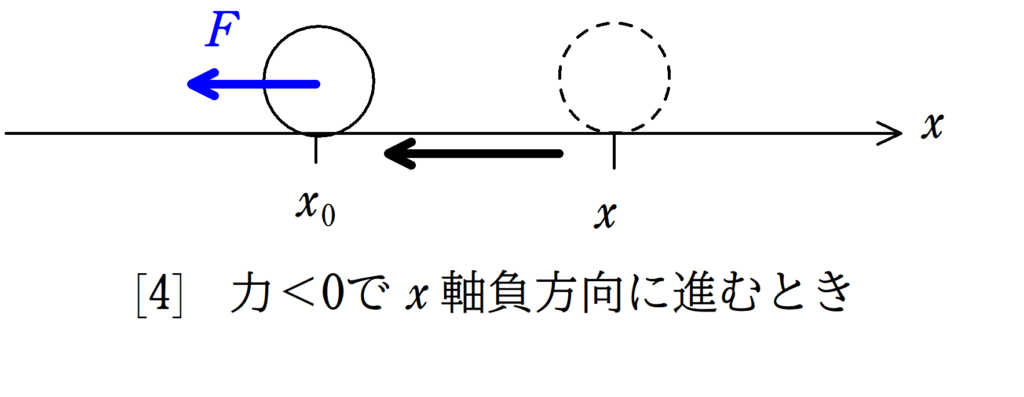

このとき,仕事は
$W=F(x_{0}-x)$
で,$F$が負,$x_{0}-x$が負だから$F$は正だね.

その通りです.
仕事の正負についてまとめると,次のようになります.
動いている方向と同じ方向に力がはたらけば,正の仕事.
動いている方向と反対方向に力がはたらけば,負の仕事
二次元のエネルギーの原理

次に2次元のエネルギーの原理についてです.
$x$方向,$y$方向の等加速度運動の式を書き出して,足し合わせてみましょう.
$v_{x}^{2}-v_{x0}^{2}=2a_{x}x$,$v_{y}^{2}-v_{y0}^{2}=2a_{y}y$
$v_{x}^{2}+v_{y}^{2}-(v_{x0}^{2}+v_{y0}^{2})=2(a_{x}x+a_{y}y)$

一次元運動と同様に,両辺$\dfrac{1}{2}m$をかけます.
また,$x$方向,$y$方向の運動方程式より
$ma_{x}=F_{x}$,$ma_{y}=F_{y}$
としましょう.
$\eqalign{\dfrac{1}{2}m(v_{x}^{2}+v_{y}^{2})-\dfrac{1}{2}m(v_{x0}^{2}+v_{y0}^{2})&=\dfrac{1}{2}m\cdot 2(a_{x}x+a_{y}y)\\&=ma_{x}x+ma_{y}y\\&=F_{x}x+F_{y}y}$

そして,$v^{2}=v_{x}^{2}+v_{y}^{2}$,$v_{0}^{2}=v_{x0}^{2}+v_{y0}^{2}$とします.
$v$は速さ,$v_{0}$は初速度の速さです.
また,$W_{x}=F_{x}x$,$W_{y}=F_{y}y$としましょう.
$\dfrac{1}{2}mv^{2}-\dfrac{1}{2}mv_{0}^{2}=W_{x}+W_{y}$

このとき,$\dfrac{1}{2}mv^2$や$\dfrac{1}{2}mv_{0}^{2}$を運動エネルギーといいます.
また,$W_{x}+W_{y}$が物体にする仕事です.
仕事はベクトル?スカラー?

仕事が$x$方向と$y$方向の成分があるようにみえるけど,仕事ってベクトルだったの??

いえ,仕事はスカラーです.
$W_{x}$と$W_{y}$は平行四辺形をつくって足しているわけではありませんよね?

ほんとだ!
単純に足し合わせているだけだった!
同じく,運動エネルギーもスカラーだね.
仕事のもう1つの計算

今までは,座標をとって,$x$方向と$y$方向の力×変位を計算しましたが,力を分解して物体が移動する方向の力×変位でも計算ができます.
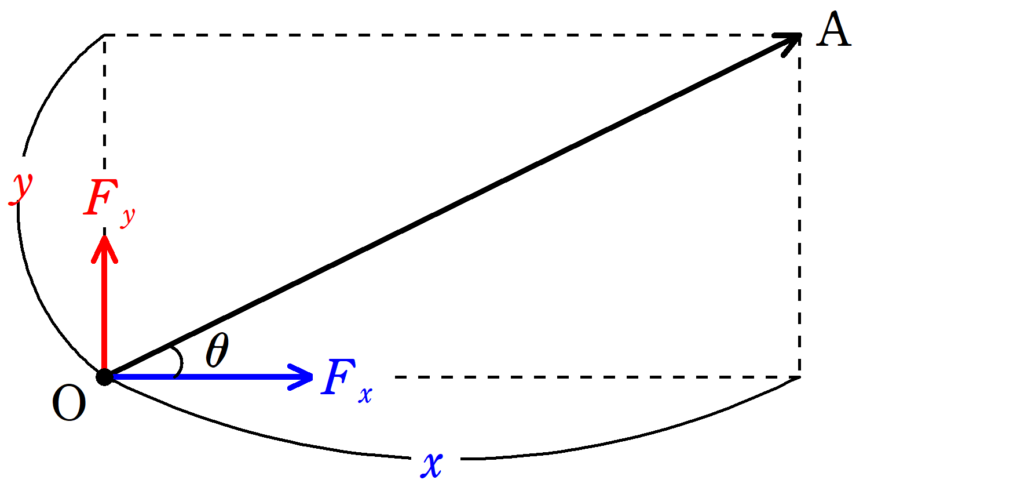
上図において,OA間で外力がした仕事$W$は
$W=F_{x}x+F_{y}y$ $\dots (\clubsuit)$
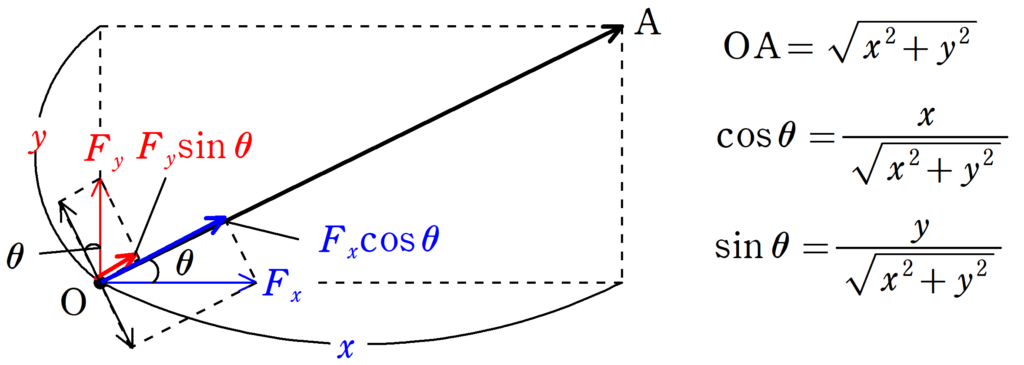
$F_{x},F_{y}$をOA方向とそれに垂直な方向に分解して仕事を計算します.
$F_{x}$のOA方向の成分は$F_{x}\cos\theta$,$F_{y}$のOA方向の成分は$F_{y}\sin\theta$なので,OA間で外力がする仕事は
$W=(F_{x}\cos\theta+F_{y}\sin\theta)\cdot {\rm OA}$
ここで,${\rm OA}=\sqrt{x^{2}+y^{2}}$,$\cos \theta=\dfrac{x}{\sqrt{x^{2}+y^{2}}}$,$\sin\theta \sqrt{x^{2}+y^{2}}$より
$\eqalign{W&=(F_{x}\cdot \dfrac{x}{\sqrt{x^{2}+y^{2}}}+F_{y}\cdot \dfrac{y}{\sqrt{x^{2}+y^{2}}})\cdot \sqrt{x^{2}+y^{2}}\\&=F_{x}x+F_{y}y}$ $\dots (\spadesuit)$

$(\clubsuit)$と$(\spadesuit)$が一緒になったね.
では,最後にエネルギーの原理と仕事についてまとめておこう!
まとめ
質量$m$の物体のAでの速さを$v_{\rm A}$,Bでの速さを$v_{\rm B}$とする.
AB間で外力が物体にした仕事を$W_{\rm AB}$とすると,次の関係が成り立つ.
$\dfrac{1}{2}mv_{\rm A}^{2}-\dfrac{1}{2}mv_{\rm B}^{2}=W_{\rm AB}$
力と変位の内積を仕事という.
内積がとっつきにくい場合は次のように考えるとよい.
① 力は一定である.もし一定でないのであれば,一定とみなせるくらい細かく分解して足し合わせる(積分する.).
② 力の方向と移動する方向が一致する場合は正の仕事,反対方向の場合は負の仕事である.
③ 力の方向と移動する方向が一直線上にない場合は,仕事の大きさについて次のどちらかで計算をする.
- 力×力の方向に移動した距離 で計算.
- 力を移動する方向に分解して計算


コメント
[…] […]
[…] […]
[…] [仕事の計算のルールはどこからくるか?]エネルギーの原理の式の導出 […]
[…] […]