
今回は重心不変の問題です.
物体系にはたらく重心の位置が変化しないことを利用して問題を解きます.
次のような問題は一度は解いたことがあるのではないでしょうか??
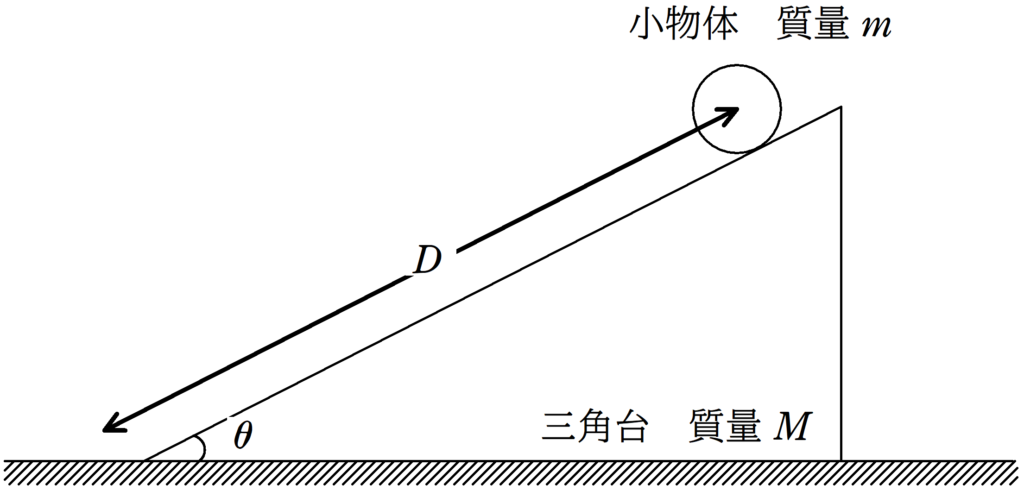
図のように水平で滑らかな床の上に質量$M$の三角台がおいてある.
三角台は傾角$\theta$の斜面をもっており,斜面はなめらかである.
いま,三角台の斜面に質量$m$の小物体おき,どちらも動かないようにおさえておく.
ある時刻において,静かに手をはなすと,小物体は斜面上を距離$D$だけ移動した.
この移動の間,三角台は静止した地面に対して水平方向にどれだけ移動するか.

まず,重心不変とはなにかを説明しましょう.
はじめ,重心が静止していて,その後,ある成分について力の和が0であるとき,その成分の重心は静止したままである.

要するに,はじめ重心が止まっていて,そこに力がはたらかないんだったら,重心は動かないで止まったままだよね,という話です.
重心に関する基礎知識は,こちらにかいてあるよ.

そもそも力の和が0になっているのかどうかを調べてみよう.
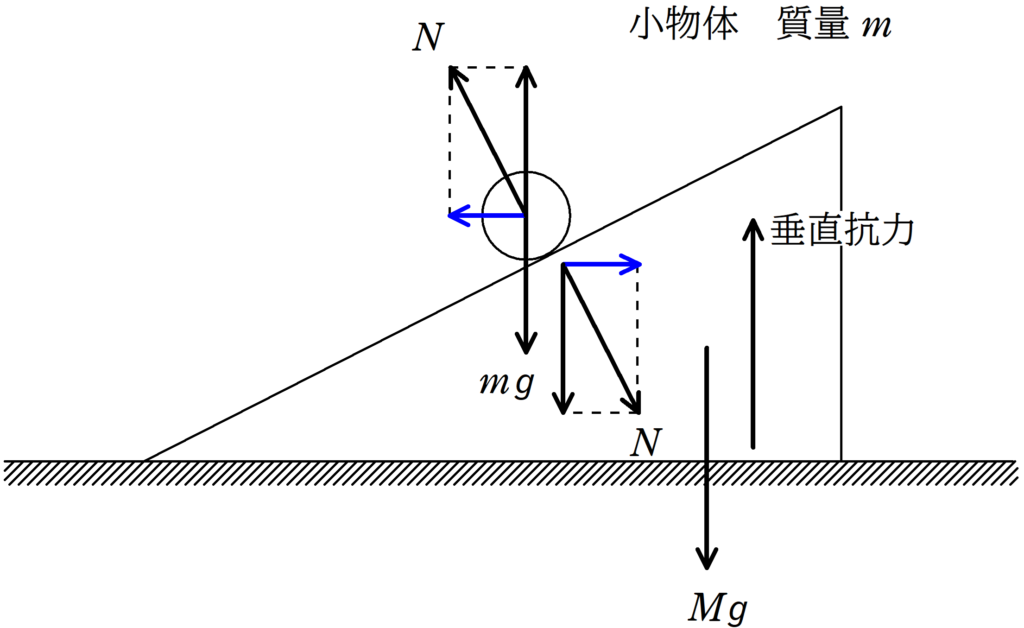

それぞれのはたらく力は次のようになるね.
★ 小物体にはたらく力
- 重力$mg$
- 斜面との垂直抗力
★ 三角台にはたらく力
- 重力$Mg$
- 斜面との垂直抗力
- 水平面との垂直抗力
このうち,水平方向にはたらく力は斜面との垂直抗力を分解したものだけですね.
作用反作用の法則より,水平成分の力の和は0となるよ.

もともと,重心は止まっていて,水平成分については力がはたらかないから,重心は止まったままなんだ.鉛直成分は静止していないよ.
静止しているもの見つけたい理由は,運動が簡単だからだよ.
なるべく簡単なところに目をつけると問題もスムーズに解けるね.
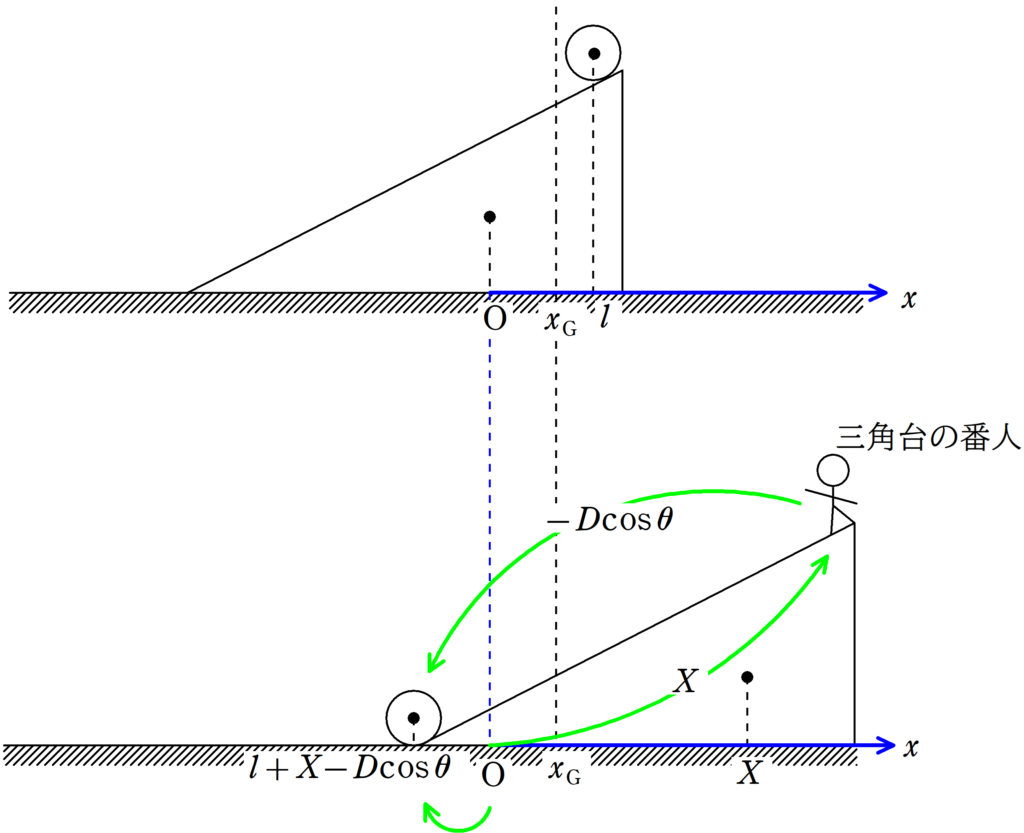

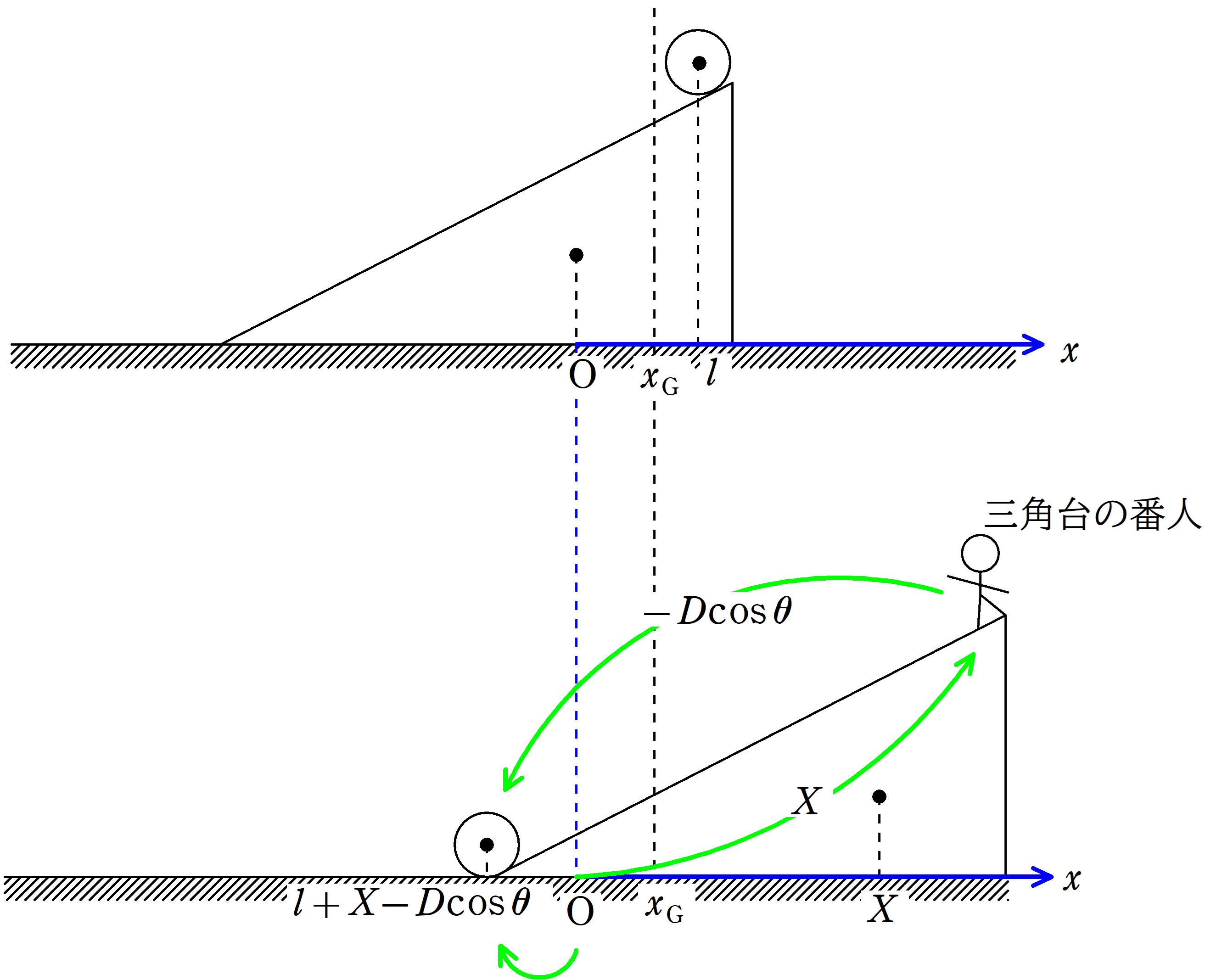
では,座標の設定からいきましょう.
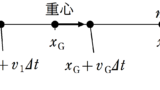
三角台がどれだけ動いたかを知りたいので,はじめの三角台の重心の位置を$x=0$として,図の右方向を正ととります.
はじめの小物体の重心の位置を$x=l$,三角台と小物体の重心の位置を$x_{\rm G}$としましょう.
また,小物体が斜面を$D$だけ下ったときの,三角台の重心の位置を$x=X$とします.
このとき,小物体の位置は次のように表すことができます.
$l+X-D\cos\theta$ $\dots (\ast)$
$(\ast)$の説明をしましょう.
★ $(\ast)$の説明
いま,とりあえず,わかっているのは,「三角台からみて小物体がDだけ下った」ということです.
水平成分のみを考えると,「$x$軸の負の向きに$D\cos\theta$だけ移動した」ともいえます.
しかし,とられている座標は地面に静止した座標です.
図の緑色の矢印をみてください.
三角台の番人は$X$だけ移動して,三角台の番人からみて小物体は$-D\cos\theta$だけ移動しています.
もともと小物体の位置は$x=l$だったので,最終的な小物体の位置は
$l+X-D\cos\theta$
となります.

それでは,小物体の移動前と移動後それぞれの重心の式を立てましょう.
★ 移動前の重心の式
$x_{\rm G}=\dfrac{M\cdot 0+m\cdot l}{M+m}$ $\dots (2\ast)$
★ 移動後の重心の式
$x_{\rm G}=\dfrac{M\cdot X+m\cdot (l+X-D\cos\theta)}{M+m}$ $\dots (3\ast)$

$(2\ast)$と$(3\ast)$より,重心不変の式を立てます.
$\eqalign{\dfrac{M\cdot X+m\cdot (l+X-D\cos\theta)}{M+m}&=\dfrac{M\cdot 0+m\cdot l}{M+m}\cr MX+m(l+X-D\cos\theta)&=ml\cr(M+m)X&=mD\cos\theta \cr X&=\dfrac{m}{M+m}D\cos\theta}$
したがって,答えは,「$\dfrac{m}{M+m}D\cos\theta$だけ右に移動する」でした.

実は,この重心不変はもう少し簡略化して計算もできるんですが,今回はちょっと真面目に式を立ててみました.
また,運動量保存則を積分するという技もあります.
これはまた,別の記事で書きたいと思います.


コメント
[…] [典型問題]重心不変 […]
[…] […]
[…] […]