平行板コンデンサーの電気容量 | Physicmath（フィジクマス）

PHYさん

今回は，平行板コンデンサーの電気容量の式の話です．

平行板コンデンサーの電気容量

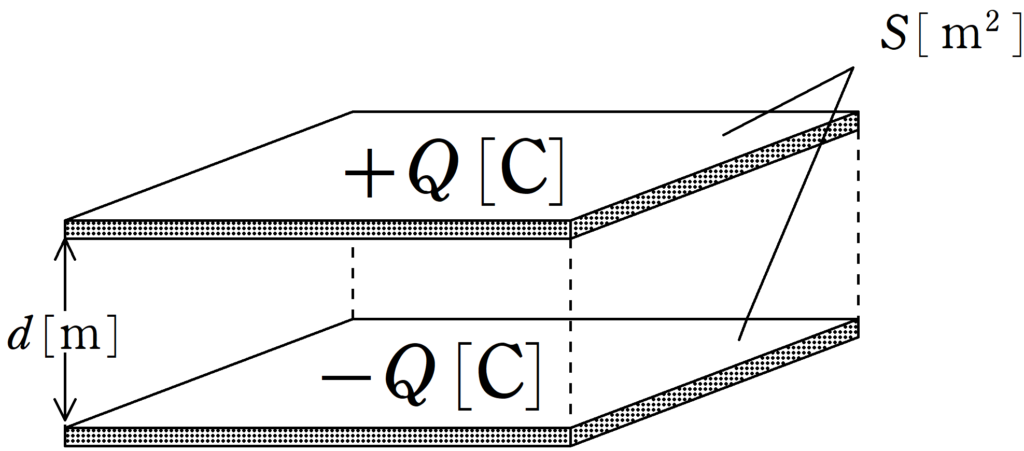
面積$S[\rm m^2]$の平らな導体板2枚を距離$d[\rm m]$だけ隔てて固定する．

真空の誘電率を$\varepsilon_{0}[\rm F/m]$とする．真空中において，このコンデンサーの電気容量$C_{0}[\rm F]$は次のようになる．

$C_{0}=\varepsilon_{0}\dfrac{S}{d}$

PHYさん

上の式を導くのに必要なことは次の3つです．

平面に一様に分布した電荷がつくる電場

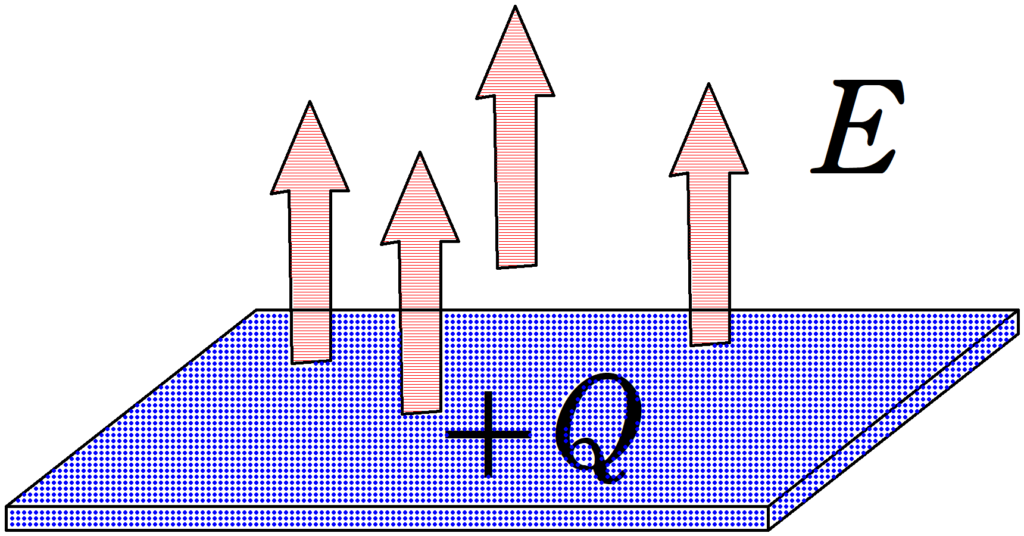
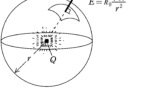
十分に広い平面に一様な電荷$Q$が分布している．

真空の誘電率を$\varepsilon_{0}$，平面の面積を$S$とするとき，電場の大きさ$E$は

$E=\dfrac{|Q|}{2\varepsilon_{0}S}$

これは，電場が距離によらず一定であることを意味している．

電場の電位差の関係

電場の大きさを$E$，距離$\Delta x$の電位差を$\Delta V$とするとき，次の関係が成り立つ．

$E=\left|\dfrac{\Delta V}{\Delta x}\right|$

電気容量の定義式

コンデンサーに蓄えられている電荷を$Q$，コンデンサー間の電圧を$V$とすれば，コンデンサーの電気容量$C$は

$C=\dfrac{Q}{V}$

実際は

$Q=CV$

として使うことが多い．

NEKO

平面に分布された電荷がつくる電場については，こちらでも説明しています．

PHYさん

それでは，これらをもとに，コンデンサーの電気容量を計算していきましょう．

PHYさん

下図のように，電荷$Q[\rm C]$と$-Q[\rm C]$が蓄えられている面積$S[\rm m^{2}]$の極板を距離$d[\rm m]$隔てて固定します．

PHYさん

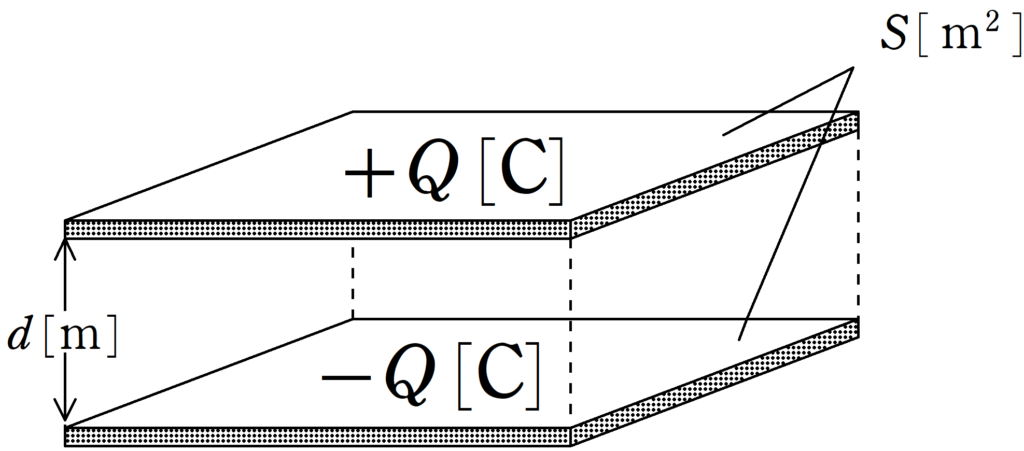
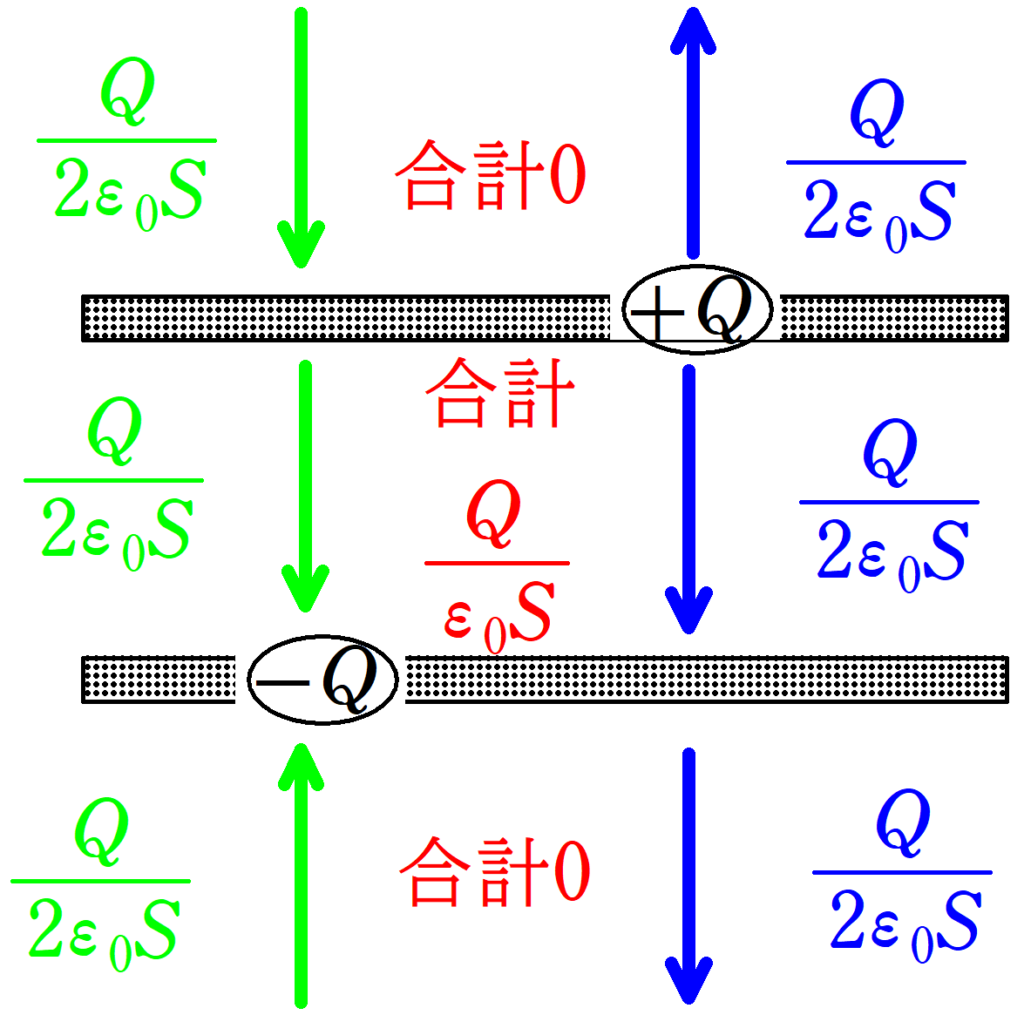
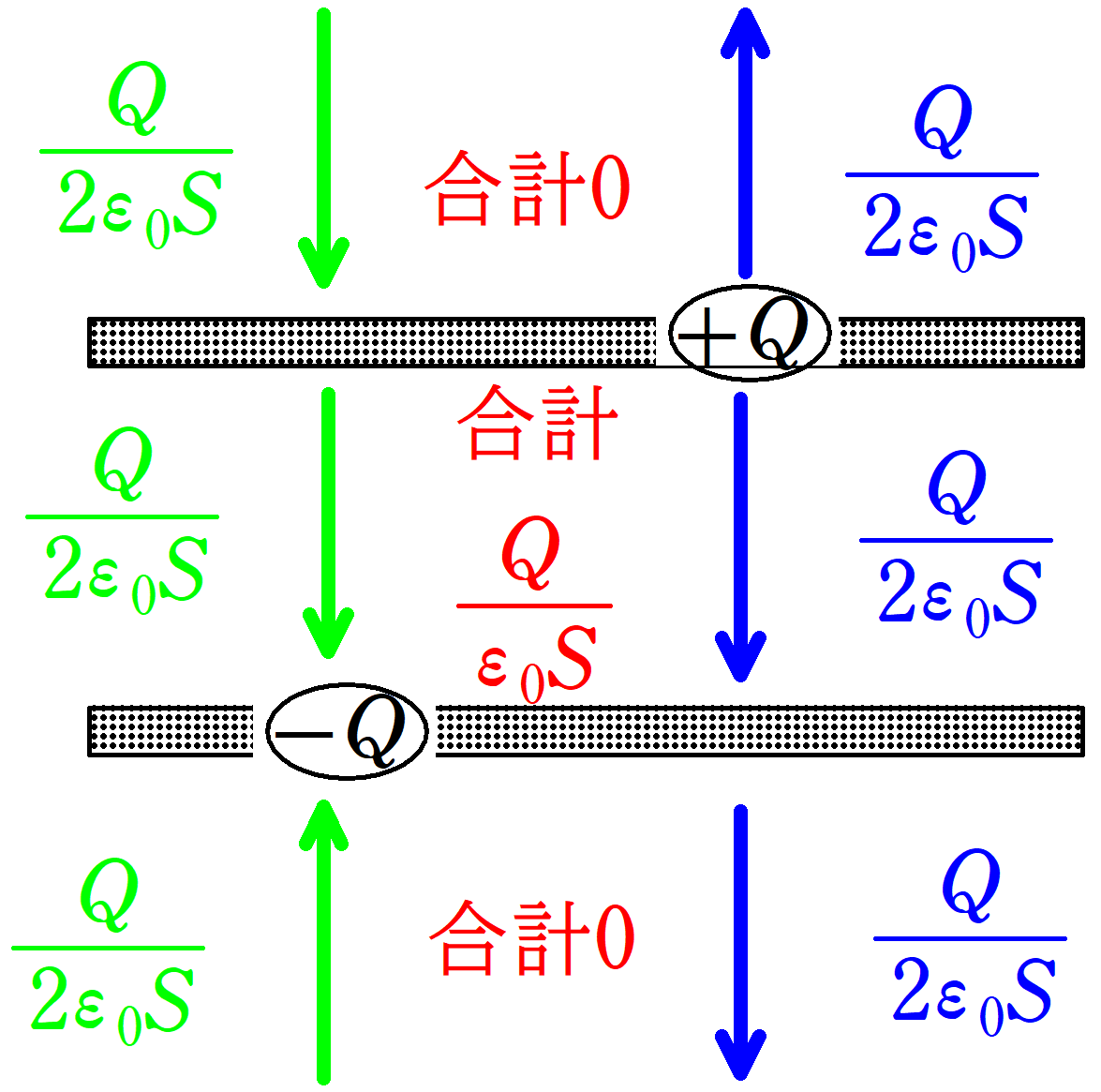
すると，$+Q$と$-Q$の電荷はそれぞれ極板の上側と下側に電場をつくります．

正の電荷からは飛び出すように電場をつくり，負の電荷は入り込むように電場をつくることに注意しましょう．

NEKO

すると，上側極板の上と下側極板の下では電場が0になって，極板の間の電場は図の下向きに$\dfrac{Q}{\varepsilon_{0}S}$となるんだね．

★　電場と電位差の関係式

コンデンサー間の電位差を$V$とすると，$E=\dfrac{V}{d}$より

$\dfrac{Q}{\varepsilon_{0}S}=\dfrac{V}{d}$

$\therefore$　$\dfrac{Q}{V}=\varepsilon_{0}\dfrac{S}{d}$　$\dots　(\ast)$

★　電気容量の定義式

$(\ast)$より

$C=\dfrac{Q}{V}=\varepsilon_{0}\dfrac{S}{d}$

NEKO

平行板コンデンサーの電気容量の式はよくでてくるので覚えておきましょう．