
今回は2020年,京都大学の入試問題の第1問を解いていきましょう.
重心の運動や相対運動を考える問題なので,やや難しく感じる人もいるかもしれません.詳しくは実際の問題を見てくださいね.
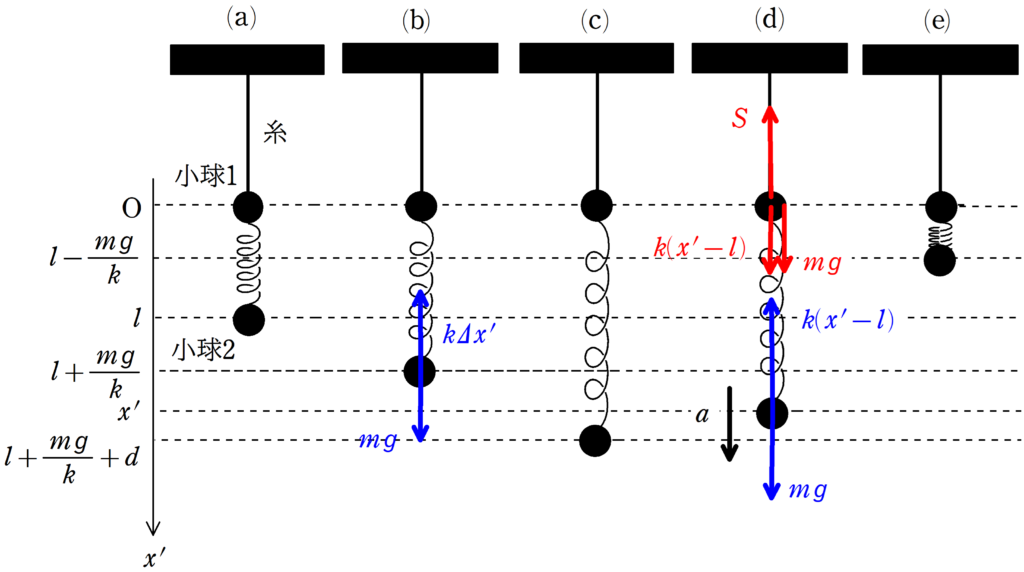

まずはどんな問題なのかを整理します.質量$m$の2つの小球があって,小球1が軽い糸につながれ,さらに小球1と小球2をばね定数$k$のばねでつなぎます.
小球1の位置を原点として,鉛直下方向の向きを正とした座標をとります.ここでは,座標を$x^{\prime}$としました.
ばねの自然の長さは$l$です.小球2をつり合いの位置から長さ$d$だけ引き下げ,静かに離すと単振動を始めます.
単振動の中心(ア)と振幅(イ)を求めよ.また,糸がたるみ始める瞬間の小球2の位置(ウ)を求め,糸がたるむための$d$の不等式を答えよ.
<解答>
小球2の位置$x^{\prime}$における加速度を$x^{\prime}$の正の向きに$a$と設定しましょう.図(d)のように自然長より伸びている状況を想定すると,重力は正の向きに$mg$,弾性力は負の向きに$k(x-l)$です.したがって,運動方程式は
$ma=-k(x^{\prime}-l)+mg=-k(x^{\prime}-l-\dfrac{mg}{k})$
となるので,中心が$l+\dfrac{mg}{k}$,角振動数$\sqrt{\dfrac{k}{m}}$,周期$2\pi\sqrt{\dfrac{m}{k}}$の単振動をすることがわかります.したがって,中心の位置は$l+\dfrac{mg}{k}$(ア).ちなみに,中心の位置とつり合いの位置は同じです.
つり合いの位置から$d$だけ引き下げて静かに離したので,スタートで振動の端でもある$x^{\prime}=l+\dfrac{mg}{k}+d$と振動の中心$l+\dfrac{mg}{k}$との距離は$d$.これが振幅ですね.$d$(イ)
また,小球2の位置が$x^{\prime}$のときの小球1にはたらく力について考えていきましょう.糸の張力の大きさを$S$として,つり合いの式を立てます.小球1のはたらく力は正の向きに弾性力$k(x-l)$と重力$mg$,負の向きに張力$S$がはたらきます.小球2のつり合いの式より
$\eqalign{k(x^{\prime}-l)+mg-S&=0\cr S&=k(x^{\prime}-l)+mg}$ $\dots (\ast)$
$(\ast)$より$x^{\prime}$が小さくなっていくと$S$が小さくなっていくのがわかります.糸がたるむのは$S=0$なので,$(\ast)$より
$\eqalign{0&=k(x^{\prime}-l)+mg\cr x^{\prime}&=l-\dfrac{mg}{k}}$
したがって,$l-\dfrac{mg}{k}$(ウ)のとき糸がたるみます.
振動の中心とたるむ位置$l-\dfrac{mg}{k}$との距離は
$l+\dfrac{mg}{k}-(l-\dfrac{mg}{k})=\dfrac{2mg}{k}$
なので,たるむための条件は$\dfrac{2mg}{k}$が$d$より小さいときです.すなわち$d>\dfrac{2mg}{k}$(エ)

次に$d$が十分大きく糸がたるむ場合のときを考えます.小球1,2の位置をそれぞれ$x_{1} , x_{2}$として,重心の位置は$\dfrac{x_{1}+x_{2}}{2}$(質量が同じなのでこの形になります.),小球1からみた小球2の相対位置$x=x_{1}-x_{2}$が設定されていています.
実際の問題ではもう少しヒントが書いてありますが,ざっと書くと次のような問いがあります.
・糸がたるみはじめたときの重心の速さを求めよ.(オ)
・小球1からみた小球2の単振動の周期を求めよ.(カ)
・小球1の速度が最小値をとる瞬間において,小球1からみた小球2の相対速度を求めよ.(キ)
<解答>
$(\ast)$の運動方程式$ma=-k(x^{\prime}-l-\dfrac{mg}{k})$を単振動のエネルギー保存の形にすると
$\dfrac{1}{2}mv^2+\dfrac{1}{2}k(x^{\prime}-l-\dfrac{mg}{k})^{2}=一定$ $\dots (\clubsuit)$
となります.図の(c)(手を離した瞬間)と(d)(糸がたるむ瞬間)(このときの小球2の速さを$v_{2}$とします.)における$(\clubsuit)$の式を立てれば,
$\eqalign{\dfrac{1}{2}m\cdot 0^{2}+\dfrac{1}{2}kd^2&=\dfrac{1}{2}mv_{2}^{2}+\dfrac{1}{2}k(\dfrac{2mg}{k})^2\cr v_{2}&=\sqrt{\dfrac{k}{m}\{d^{2}-(\dfrac{2mg}{k})^{2})\}}}$
したがって,糸がたるむ瞬間の重心の速度は$\dfrac{-v_{2}+0}{2}$なので,重心の速さは$\dfrac{1}{2}\sqrt{\dfrac{k}{m}\{d^{2}-(\dfrac{2mg}{k})^{2})\}}$(オ)
また,糸がたるんだ後の小球1からみた小球2の位置$x$における加速度を$a_{12}$,小球1の加速度を$a_{1}$として,小球1の運動方程式と小球1からみた小球2の運動方程式を立てます.後者は慣性力がかかることに注意です.
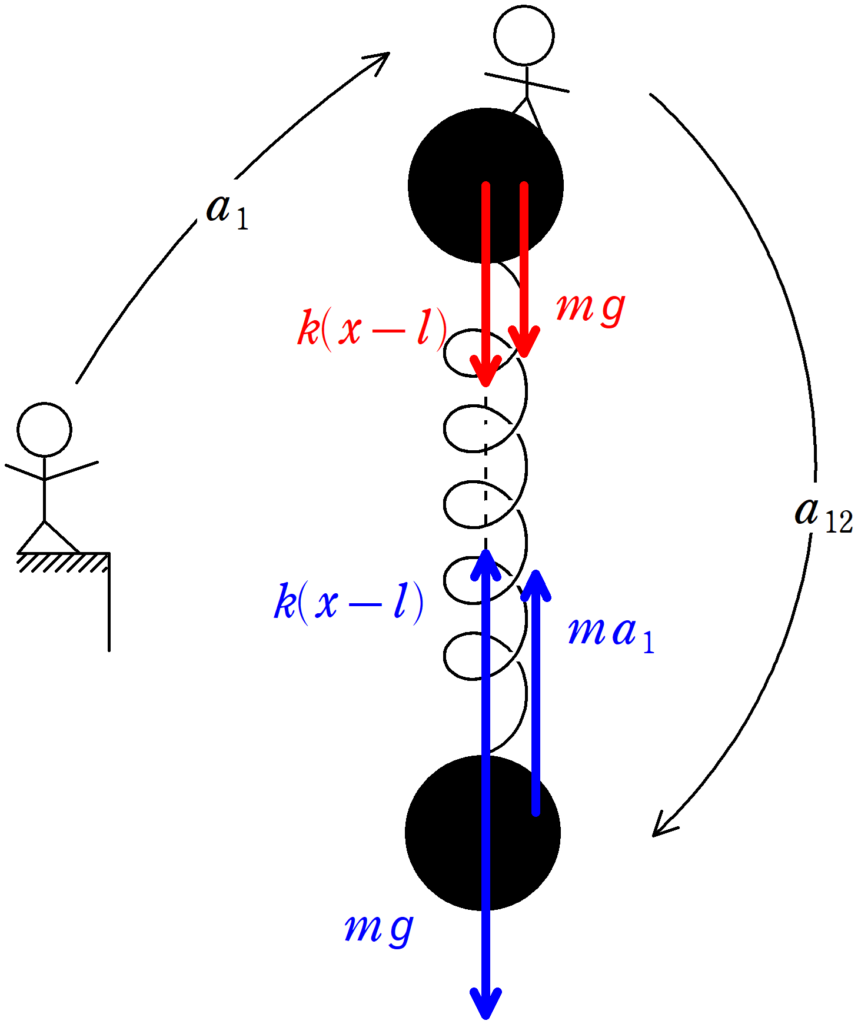
$ma_{1}=mg+k(x-l)$ $\dots (2\ast)$
$ma_{12}=mg-k(x-l)-ma_{1}$ $\dots (3\ast)$
$(2\ast)$,$(3\ast)$より,$a_{1}$を消去して$a_{12}$を求めると
$\eqalign{ma_{12}&=mg-k(x-l)-\{mg+k(x-l)\}\\ &=-2k(x-l)}$
したがって,小球1からみた小球2は単振動をし,その周期は$2\pi\sqrt{\dfrac{m}{2k}}$(カ)となります.
次に小球1の速度が最小となるときのことを考えましょう.まず,糸がたるんだ瞬間の小球1の速度は0です.また,$(2\ast)$より,小球1の加速度$a_{1}$は
$a_{1}=g+\dfrac{k}{m}(x-l)=\dfrac{k}{m}x-\dfrac{k}{m}l+g$
です.糸がたるんだ瞬間の加速度は$(4\ast)$より$x=l-\dfrac{mg}{k}$を代入して,0になります.その後,$x$が小さくなる(ばねが縮む)ので,小球1の加速度は負になります.すると,小球1は負の速度をもち,加速度が負のときは負の速度の絶対値がどんどん大きくなっていきます.そして,再び小球1の加速度が0になるところで,小球1の速度が最小となります.
したがって,$(4\ast)$より,再び加速度が0になる$x$は
$x=l-\dfrac{mg}{k}$
のときです.これは糸がたるんだときの小球1からみた小球2の位置と同じなので,速さも同じです.速度は逆向きになりますね.したがって,小球1からみた小球2の速度は,$\sqrt{\dfrac{k}{m}\{d^{2}-(\dfrac{2mg}{k})^{2})\}}$となります.答えは重心の速さを用いて穴埋めなので正確には$2$(キ)

次に図のように質量$m$の2つの小球をばねと糸でつるします.ばねが自然長のときの小球1の位置を原点として,鉛直下向きを座標軸の正の向きをとります.
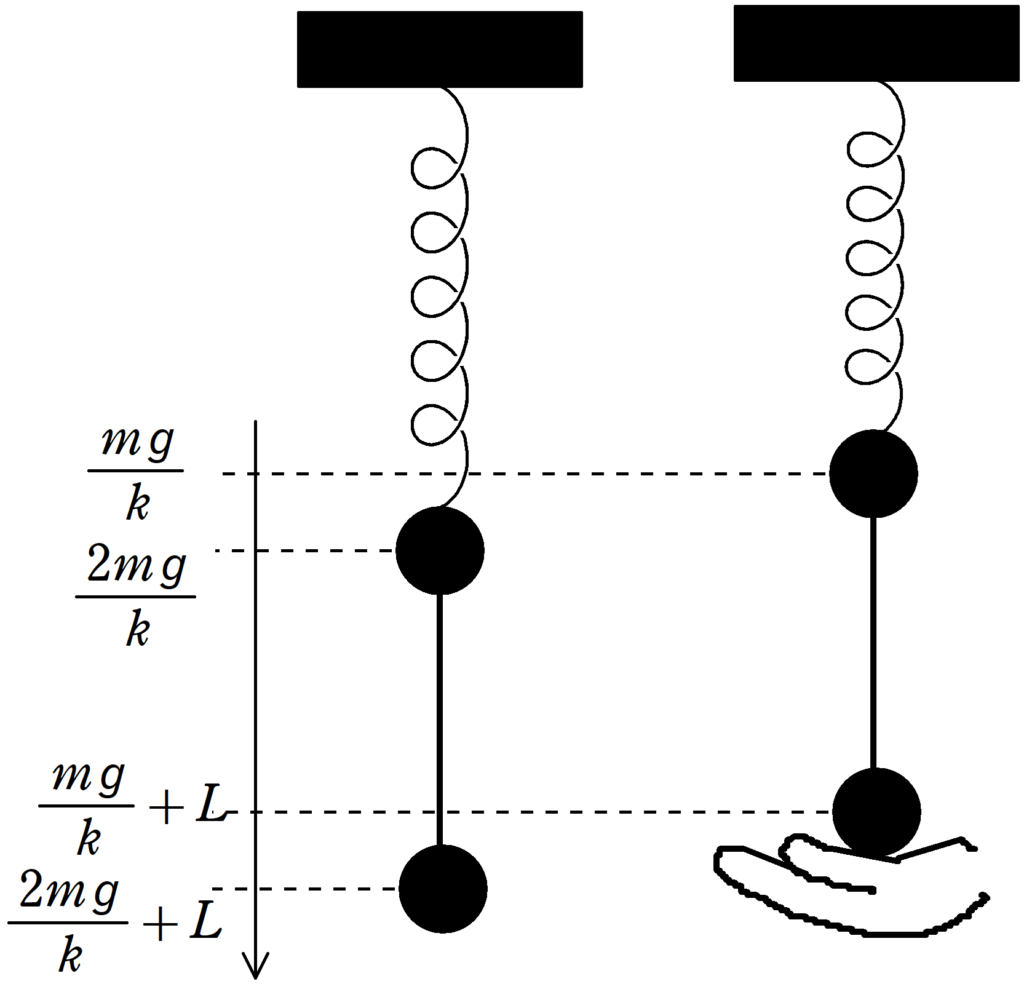

糸の長さは$L$です.何も力を加えていないときの小球1の座標は小球1に関するつり合いを考えれば,自然長からのばねの伸びを$\Delta x_{1}$として
$k\Delta x_{1}=2mg$ $\therefore \Delta x_{1}=\dfrac{2mg}{k}$
となります.で,今回は小球2を手で支えて糸がたるまない,かつ張力が0のときからスタートします.この状態から時刻0に小球2を上方に速さ$v$で打ち上げます.
・時刻0のときの小球1の位置を答えよ.(ク)
・打ち上げ後に小球2は小球1に衝突せずに落下に転じる場合を考える.小球2が落下し,打ち上げられた位置に戻ってきたときに,糸のたるみがなくなる.たるみがなくなる前後で力学的エネルギーは保存されるものとするとき,たるみがなくなった直後の小球2の速度(ケ)を求めよ.
・その後,小球1は単振動をはじめる.その振幅を求めよ.(コ)
<解答>
時刻0のときに小球にはたらくのは弾性力と重力のみです.問題文に書かれている通り張力ははたらかないので,小球1の位置はつりあいの式を考えて$\dfrac{mg}{k}$(ク)
たるみがなくなる直前の速度は$v$であり,たるみがなくった直後の小球1と2の速度をそれぞれ$v_{1}$,$v_{2}$として,力学的エネルギー保存則と運動量保存則より
$\dfrac{1}{2}mv^{2}=\dfrac{1}{2}mv_{1}^{2}+\dfrac{1}{2}v_{2}^{2}$
$mv=mv_{1}+mv_{2}$
以上2式を解いて,$v_{2}=v$または$0$を得るが,糸のたるみがなくった直後は糸を介して撃力がはたらくため,速度の変化が起こるから$v_{2}=v$は不適.したがって,$v_{2}=0$(ケ)(力学的エネルギーが保存する完全弾性衝突とみなして解くのもあり)
すると,再び糸がたるみ,小球は重力と弾性力を受けて単振動を始める.その後小球1の位置$x_{1}$における加速度を$a_{1}$として運動方程式を立てると
$ma_{1}=mg-kx=-k(x-\dfrac{mg}{k})$
より,中心がはじめにいた位置$\dfrac{mg}{k}$の単振動をする.単振動のエネルギー保存より速度が0となる位置を$x=A$として($A$が振幅です)
$\eqalign{\dfrac{1}{2}mv^{2}+\dfrac{1}{2}k\cdot 0^{2}&=\dfrac{1}{2}m\cdot 0^{2}+\dfrac{1}{2}kA^2\cr A&=v\sqrt{\dfrac{m}{k}}}$
したがって,振幅は$v\sqrt{\dfrac{m}{k}}$(コ)

次に,打ち上げ後に小球2が落下せず小球1と弾性衝突する場合を考えます.
・衝突直後の小球1の速さ$v^{\prime}$を求めよ.(サ)
・衝突後,2つの小球は糸がたるんだまま運動し,小球1が衝突時の位置に戻るまでのある時刻$T$に糸のたるみがなくなった.その直後からしばらくの間,糸のたるみがないまま運動が続く条件を考える.衝突の直前後で力学的エネルギーが保存されるものとして,時刻$T$の直後に糸がたるまないためには,時刻$T$の直前の小球1からみた小球2の速度は(シ)でなければならない.
・小球1にはたらくばねの力$F$は,時刻$T$の直前に$F\geqq 0$である.一方,時刻$T$には糸のたるみがないため張力が0以上であるが,そのとき$F>0$ならば直後に糸がたるんでしまう.以上より,時刻$T$における小球1の位置を求めよ.(ス)
・2つの小球の力学的エネルギーが,衝突後から時刻$T$の間はそれぞれ保存することを考えて,打ち上げの速さ$v$の関係式$v^2$=(セ)を求めよ.
<解答>
小球2が小球1と衝突する直前の速さは$v_{2}$は,力学的エネルギー保存則より
$\dfrac{1}{2}mv^{2}=\dfrac{1}{2}mv_{2}^{2}+mgL$
$\therefore v_{2}=\sqrt{v^{2}-2gL}$
衝突直後の小球1と小球2の速度を$v_{1}^{\prime}$,$v_{2}^{\prime}$とします.運動量保存則と反発係数の式より
$m(-v_{2})=mv_{1}^{\prime}+mv_{2}^{\prime}$
$1=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{0-(-v_{2})}$
以上2式から$v_{1}^{\prime}=-v_{2}$を得る.(いわゆる速度交換が起こります)したがって$v^{\prime}=|-v_{1}^{\prime}|=\sqrt{v^{2}-2gL}$.$v^{\prime}=\sqrt{v^{2}-2gL}$(サ)
糸のたるみがなくなる前後で力学的エネルギーが保存するので,弾性衝突とみなすことができます.すると,質量が同じなので速度交換が起こります.速度交換が起こると結局(コ)のとき考えたようにほとんどの場合再び糸がたるんでしまいます.
しかし,小球1と小球2が同じ速度であれば,再び糸がたるむことはありません.したがって,時刻$T$の直前の小球1からみた小球2の速度は$0$(シ)
(ス)は問題文をよく読めば$0$(ス)であることはすぐにわかると思います.ただ,問題文に書かれていることがやや難しいので,解説をしておきます.
時刻$T$の後,糸がたるむことなく運動したときを考えます.張力の大きさを$S$,弾性力を$F$,2つの小球の加速度を$\beta$とすると,運動方程式は
$m\beta =mg+S+F$,$m\beta =mg-S$
以上より,$S=-\dfrac{1}{2}F$.時刻$T$の直前はばねは伸びていたので$F\geqq 0$.$S=-\dfrac{1}{2}F$の関係より,糸がたるまないためには$F\leqq 0$これを同時にみたすのは$F=0$つまり,ばねが自然長になったときに時刻$T$をむかえるときです.
最後の(ス)は力学的エネルギー保存則を立てて求めます.まず,情報を整理すると次の図のようになります.
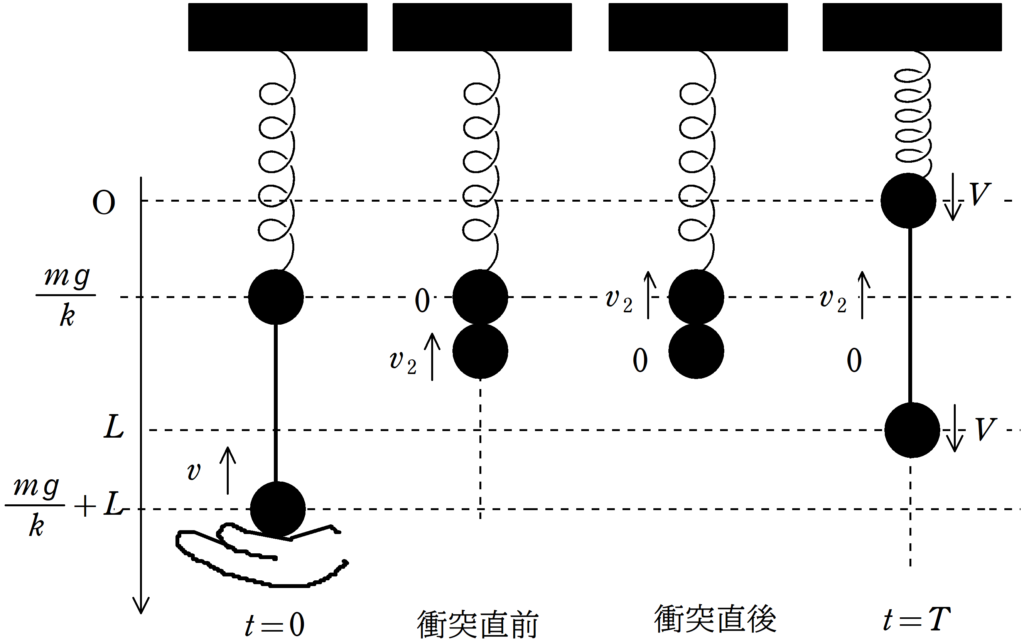
衝突直後と$t=T$直前について小球1と小球2の力学的エネルギー保存則を立てます.すでに求めている通り,$v_{2}=\sqrt{v^{2}-2gL}$です.また,$t=T$直前の小球1と小球2の速さをともに$V$とします.
まずは小球1について,重力による位置エネルギーの基準点は衝突直後の位置としています.
$\dfrac{1}{2}mv_{2}^{2}+\dfrac{1}{2}k(\dfrac{mg}{k})^{2}=\dfrac{1}{2}mV^{2}+mg\cdot \dfrac{mg}{k}$
次に小球2について,重力による位置エネルギーの基準点を$t=T$のときの位置として
$mg(L-\dfrac{mg}{k})=\dfrac{1}{2}mV^2$
以上2式から$V^2$を消去して
$v^2=4gL-\dfrac{mg^{2}}{k}$(セ)

最後のグラフ以外の問題を解説してみました.かなり量が多いので,手際よく処理しなくてはいけないですね.
普段から状況を把握するために図をかいて考える癖をつけましょう.そして,京都大の問題に慣れるためには京都大の過去問をやるのが一番です.問題文に書かれているヒントを確実に読めるように練習しましょう!



コメント