導体棒のグラフ対策5 | Physicmath（フィジクマス）

PHYさん

前回の内容はこちらです．

問題

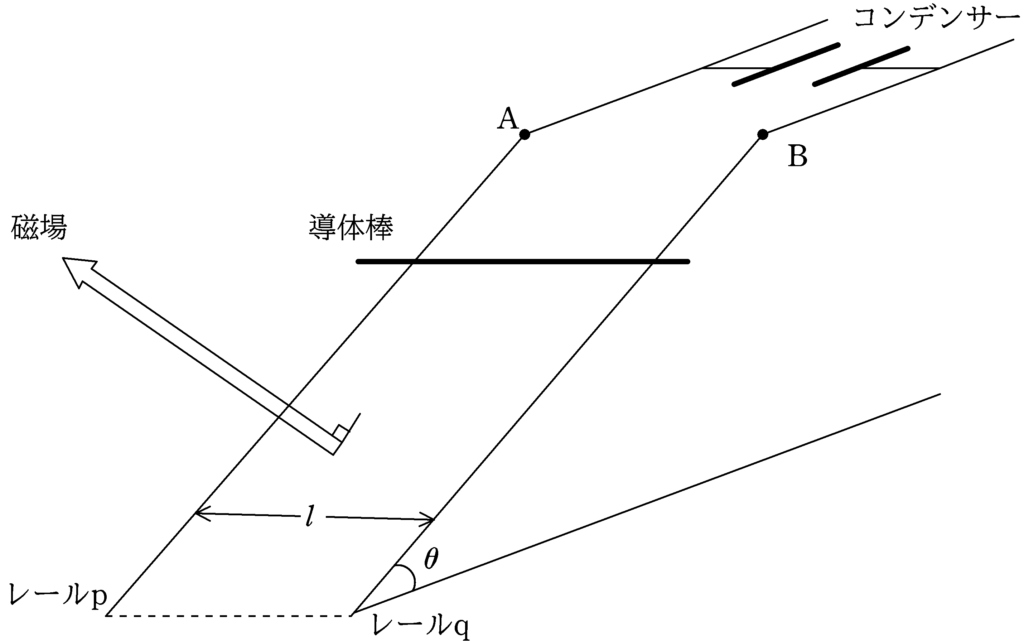
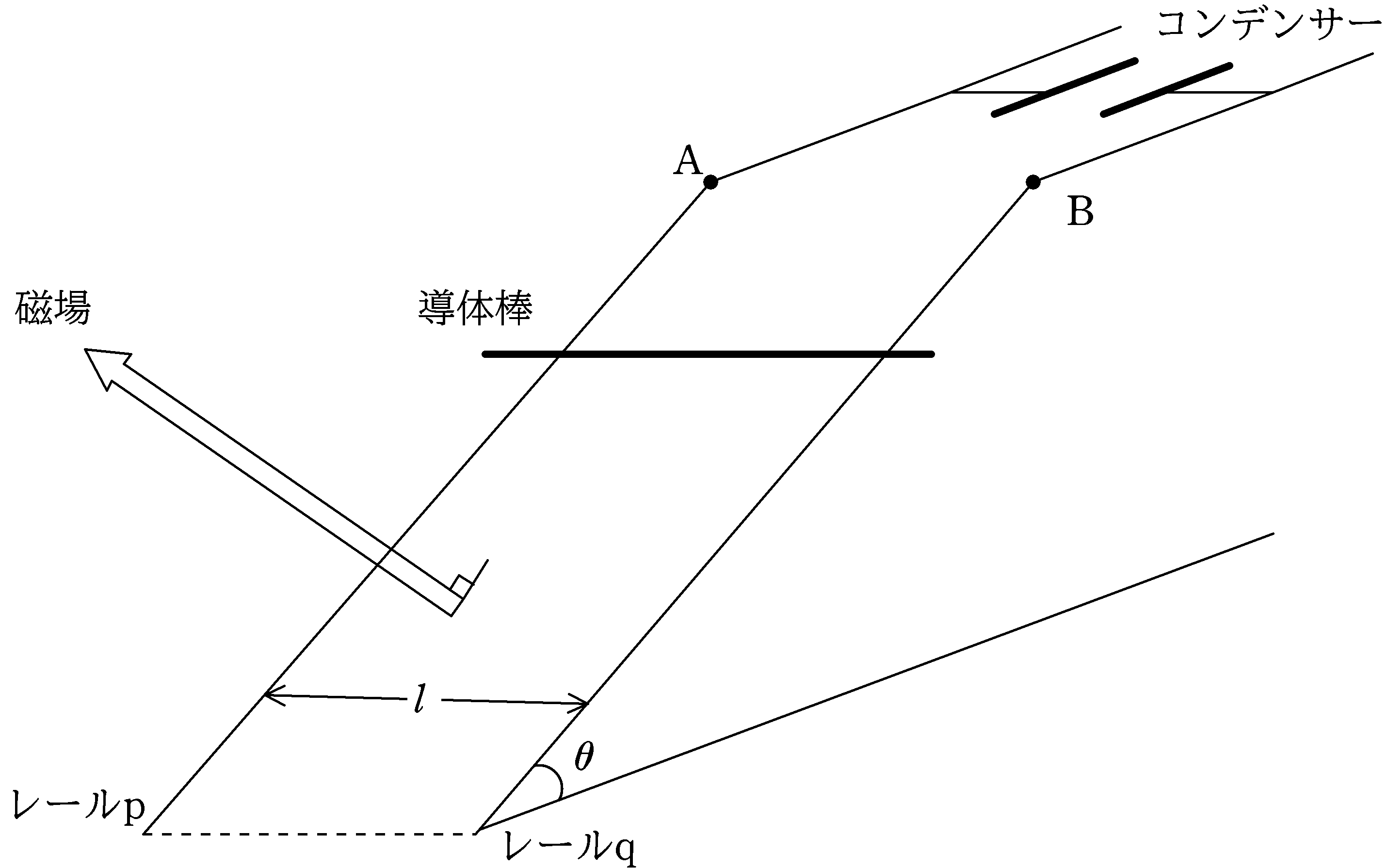
図のように，傾角$\theta$の斜面上に導体レールp，qが距離$l$を隔てて平行に固定されている．また，レールp，qは導線によって，電気容量$C$の帯電していないコンデンサーに接続されている．

図のように磁束密度の大きさ$B$の磁場を斜面に垂直な方向にかけ，質量$m$の導体棒をレールp，qに垂直になるように，静止させておく．

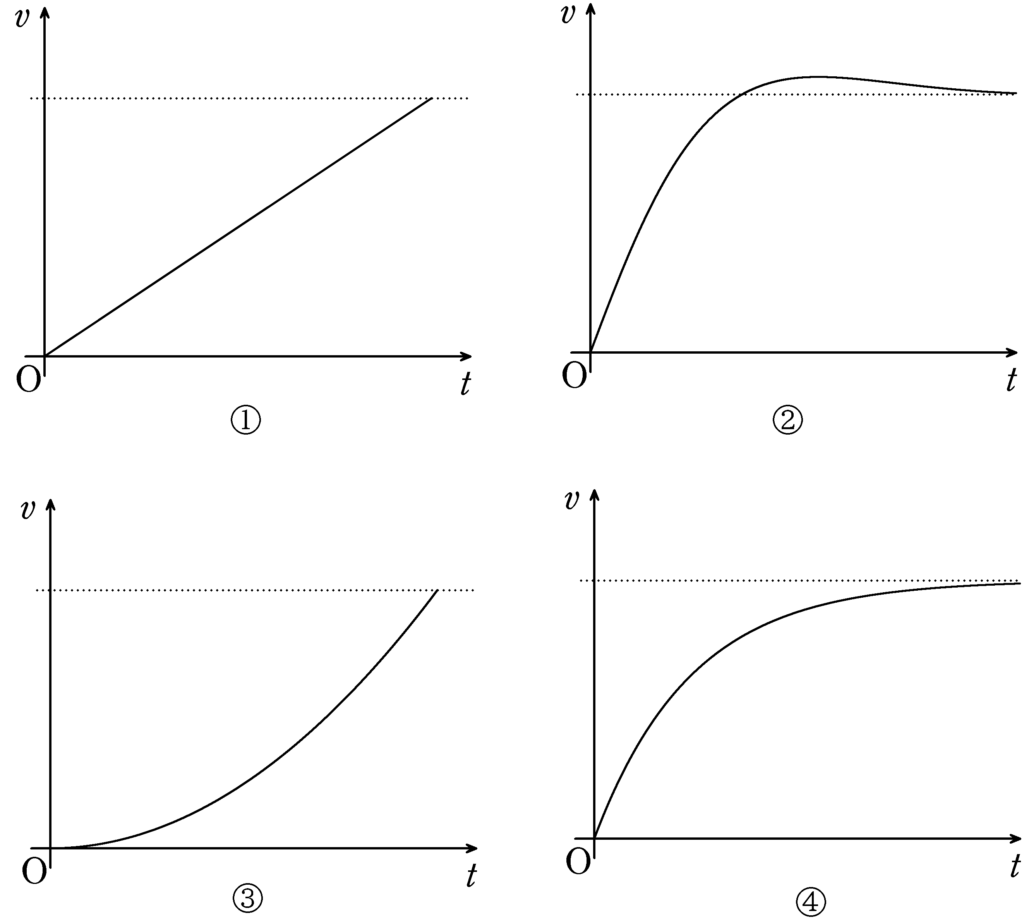
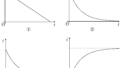
導体棒のおさえを取り除くと導体棒は動き始めた．動き始めたときの時刻を$0$としたとき，縦軸を導体棒の速度$v$，横軸を時刻$t$としたときのグラフとして適当なものを次の①~④の中から選べ．

ただし，導体棒とレールp，qの間に摩擦力がはたらかないとし，重力加速度の大きさを$g$とする．

導体棒に生じる誘導起電力の公式（直線運動）

PQ間に生じる誘導起電力の大きさ$V_{\rm{PQ}}$は，PQの長さを$l$，PQ方向に垂直な速さを$v_{\perp}$，導体棒が動く方向と垂直な磁束密度の大きさを$B$とすれば，

$V=v_{\perp}Bl$

導体棒の問題で立てて欲しい3つの式

電気容量の定義式

コンデンサーに蓄えられている電荷を$Q$，コンデンサー間の電圧を$V$とすれば，コンデンサーの電気容量$C$は

$C=\dfrac{Q}{V}$

実際は

$Q=CV$

として使うことが多い．

NEKO

今回も，キルヒホッフ則と運動方程式を立てましょう．また，コンデンサーがからむ問題なので，電流の定義式も立てます．

NEKO

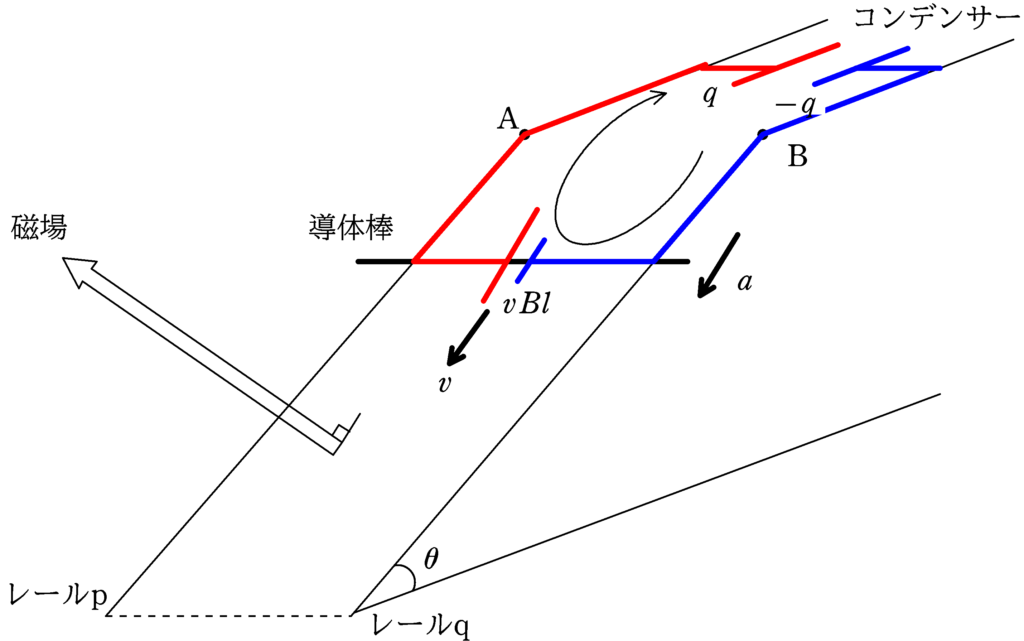
導体棒の速度を$v$としたとき，導体棒に生じる誘導起電力の大きさは$vBl$です．

回路に流れる電流を図の向きに$i$として，コンデンサーに蓄えられている電荷を$q$としましょう．また，導体棒の加速度は$a$とします．

★　キルヒホッフ則（コンデンサーの基本式）

$q=C\cdot vBl　\cdots (\ast)$

★　電流の定義式

$i=\dfrac{\varDelta q}{\varDelta t}$　$\cdots (2\ast)$

NEKO

$(\ast)$と$(2\ast)$より，$q$を消去すると（次に立てる運動方程式に代入するため）

$\eqalign{i&=\dfrac{\varDelta (CvBl)}{\varDelta t}\\&=CBl\cdot \dfrac{\varDelta v}{\varDelta t}}$

加速度の定義を用いれば

$\dfrac{\varDelta v}{\varDelta t}=a$

なので

$i=CBla$　$\cdots (3\ast)$

だね．

NEKO

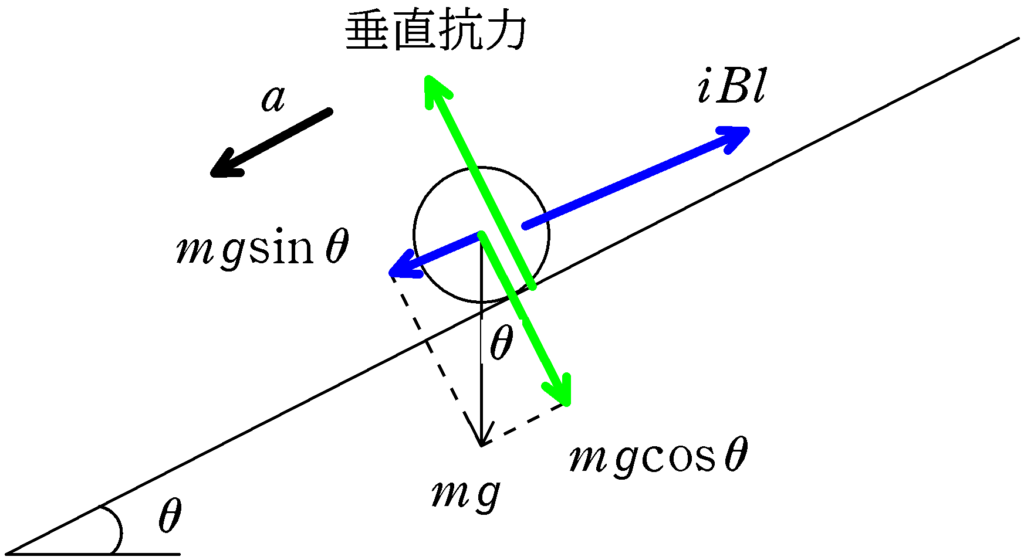
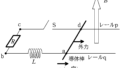
導体棒にはたらく力は上図です．

斜面に平行な成分は重力の斜面平行成分$mg\sin\theta$と，電磁力$iBl$となります．

★　運動方程式

運動方程式を立てて，$(3\ast)$を代入すると

$\eqalign{ma&=mg\sin\theta-iBl\\&=mg\sin\theta-CBla\cdot Bl\\&=mg\sin\theta-CB^{2}l^{2}a}$

$a$についてまとめて

$(m+CB^{2}l^{2})a=mg\sin\theta$

$a=\dfrac{mg\sin\theta}{m+CB^{2}l^{2}}=一定$

NEKO

$a$が一定なので，導体棒は等加速度運動をするんだね．

$v-t$グラフの傾きが加速度だから，傾きが一定の直線になるんだね．つまり，答えは①（答）