
2021年の共通テストの第2日程では,実験とからめた問題が何問かでてきました.
今回は,グラフを読み取る問題について扱いたいと思います.
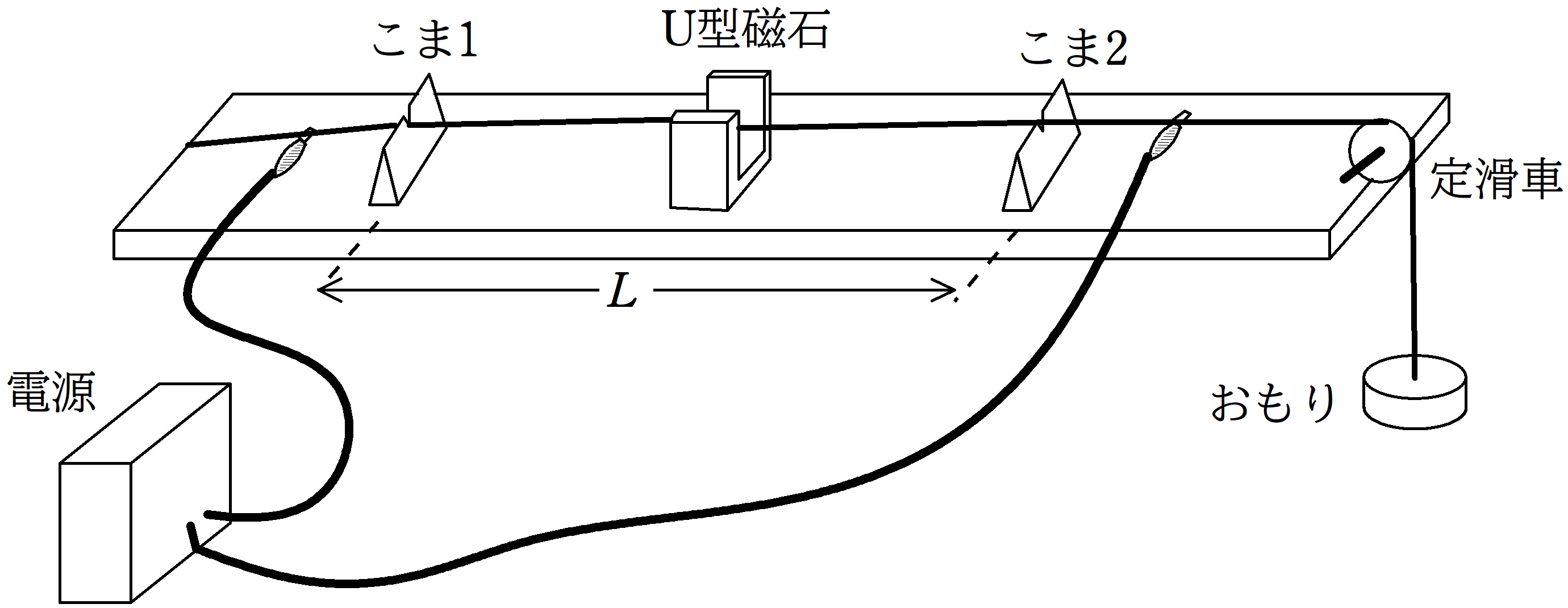
図のような装置を使って,弦の定常波(定在波)の実験をした.金属製の弦の一端を板の左端に固定し,弦の他端におもりを取り付け,板の右端にある定滑車を通しておもりをつり下げた.そして,こま1とこま2を使って,弦を板から浮かした.さらに,こま1とこま2の中央にU型磁石を置き,弦に垂直で水平な磁場がかかるようにした.そして,弦に交流電源を流した.電源の交流周波数は自由に変えることができる.こま1とこま2の間隔を$L$とする.ただし,電源をつないだことによる弦の張力への影響はないものとする.
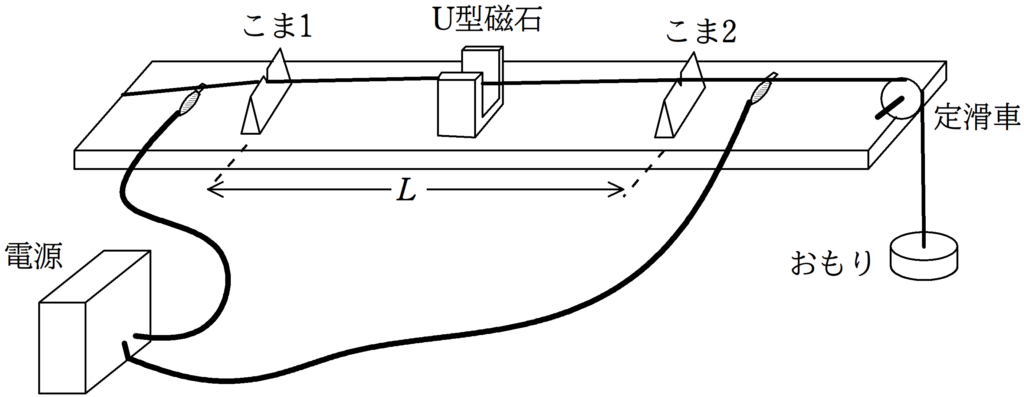
弦に交流電流を流して,腹1個の定常波が生じたときの交流周波数$f$を測定した.これは,交流周波数と弦の基本振動数が一致して共振を起こした結果である.U型磁石が常に中央にあるように,こま1とこま2の間隔$L$を変えながら実験を行い,縦軸に基本振動数$f$,横軸に$\dfrac{1}{L}$を取って,下図のようなグラフを作成した.下の問いに答えよ.
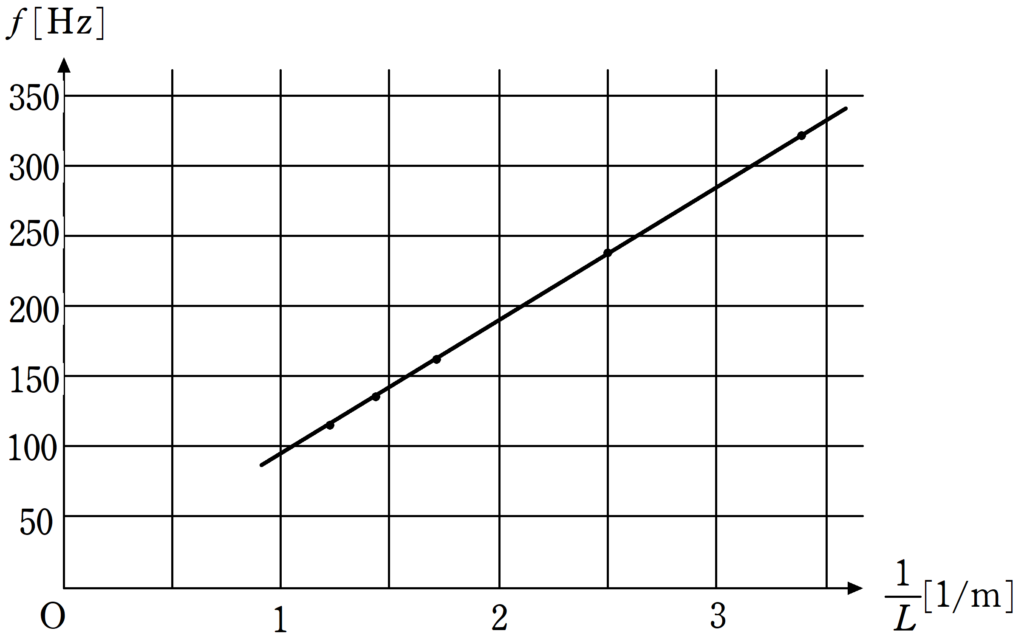
問1 $L=0.50\rm m$の弦の基本振動数は何$\rm Hz$か.最も適当な数値を次の①~⑥のうちから一つ選べ.$\fbox{ 14 }$$\rm Hz$
① $50$ ② $90$ ③ $1.7×10^{2}$
④ $1.9×10^{2}$ ⑤ $2.7×10^{2}$ ⑥ $3.1×10^{2}$
問2 弦を伝わる波の速さは何$\rm m/s$か.次の空欄$\fbox{ 15 }$~$\fbox{ 17 }$に入る数字として最も適当なものを,下の①~⓪のうちから一つずつ選べ.ただし,同じものを繰り返し選んでもよい.
$\fbox{ 15 }.\fbox{ 16 }×10^{\fbox{17}}$$\rm m/s$
① $1$ ② $2$ ③ $3$ ④ $4$ ⑤ $5$
⑥ $6$ ⑦ $7$ ⑧ $8$ ⑨ $9$ ⓪ $0$
<解答>

弦に交流電流を流すと,U型磁石内にある弦の部分に電磁力がはたらきます.
しかもその電磁力は電流の大きさと向きが変化するので,その変化に伴い電磁力も大きさ向きが変化します.
弦に力を加えるタイミングが悪いと,定常波はできません.
ブランコに乗っている人を後ろからおしてあげるときにタイミングよくおせば,ブランコは大きく振動しますが,おすタイミングを間違うと,ブランコはやがて止まってしまいます.
大きく振動するタイミングは,波の伝わる速さや波長によって変化します.
この問題では,波が伝わる速さは変化しません.
次のことを確認しておきましょう.
線密度$\rho[\rm kg/m]$の弦に張力$S[\rm N]$の力がかかっているとき,弦の伝わる速さ$v[\rm m/s]$は,次のようになる.
$v=\sqrt{\dfrac{S}{\rho}}$

この問題では,張力も線密度も変化しません.
問題文に書かれているように,腹が1個の定常波ができたときの弦の長さ$L$測定しています.
両端が節で腹1個の定常波は,次図のようになります.
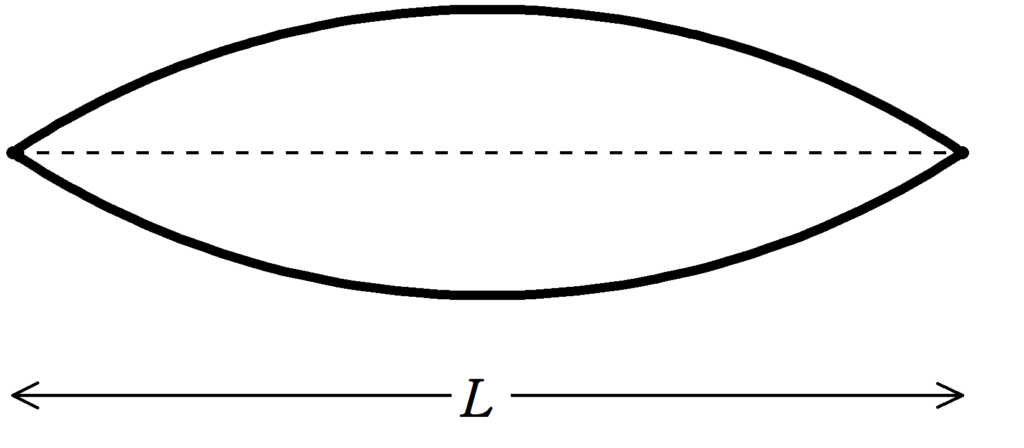

上図に定常波は波長を$\lambda$とすると,$\dfrac{\lambda}{2}$に相当します.
つまり
$L=\dfrac{\lambda}{2}$
$\therefore \lambda=2L$

さらに,波の基本式より,振動数$f$と波長$\lambda$と波が伝わる速さ$v$には次の関係があります.
振動数を$f$,波長を$\lambda$,波が伝わる速さを$v$,周期を$T$とするとき,次の関係式が成り立つ.
$v=\dfrac{\lambda}{T}=f\lambda$
★ 波の基本式
$\lambda=2L$より
$v=f\lambda=f\cdot 2L $
$f$$=\dfrac{v}{2}\cdot $$\dfrac{1}{L}$

さきほど考察したように,波が伝わる速さは変化しません.
縦軸を$f$に,横軸を$\dfrac{1}{L}$にとると,
$f$$=\dfrac{v}{2}\cdot $$\dfrac{1}{L}$
は,直線のグラフ
$y$$=a$$x$
に対応します.
つまり,$\dfrac{v}{2}$は縦軸を$f$に,横軸を$\dfrac{1}{L}$にとったグラフの傾きに対応します.
(1)
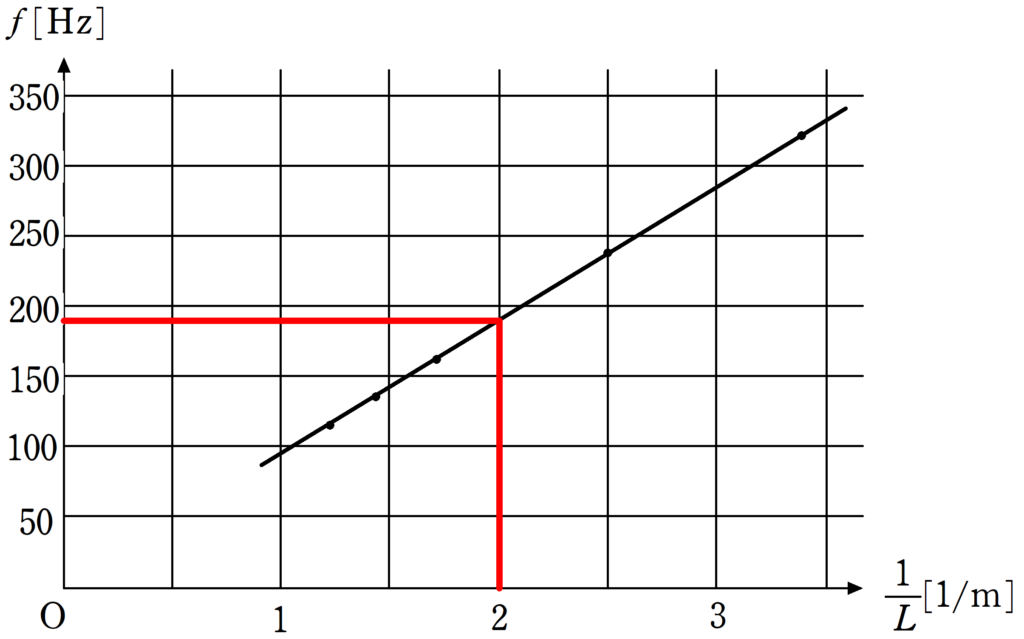

$L=0.50$のとき,$\dfrac{1}{L}=\dfrac{1}{0.50}=2.0$です.
このとき,グラフを読み取れば,振動数$f$は200よりやや小さい値であることが確認できます.
選択肢の中で最も近い値は④の$1.9×10^{2} \rm Hz$(答)$\fbox{ 14 }$ ④です.
(2)

$\dfrac{v}{2}$は縦軸を$f$に,横軸を$\dfrac{1}{L}$にとったグラフの傾きに対応します.
つまり,傾きを読み取ればよいのですが,正確な値は読み取れそうにありません.
そこで,(1)を利用しましょう.
グラフの傾きは$\dfrac{190}{2}$です.
したがって
$\dfrac{v}{2}=\dfrac{190}{2}$
$v=1.9×10^{2} \rm m/s$ (答)
$\fbox{ 15 }$ ① $\fbox{ 16 }$ ⑨ $\fbox{ 17 }$ ②


コメント