
今回は平面波の干渉の問題を扱います.
苦手な人が多いところですね.
平面波が干渉し,強め合う場所と弱め合う場所ができます.
強め合う場所を結んだ線を腹線,弱め合う場所を結んだ線を節線といいます.
腹線と腹線の距離を求めたり,腹線と節線の距離を求めたりするものがありますが,それは次回に扱いましょう.
今回は,腹線(または節線)は「タテなのか?ヨコなのか?」の話です.
タテかヨコは覚えるものでは,なくその都度考えてみるとよいでしょう.


上図の青と緑の実線は山,破線は谷です.
これらの2つの方向から来た波の干渉を考えます.
青の波と緑の波の波長,波の伝わる速さ,振幅は同じです.
また,上図の青線と緑線は黒線からのなす角が等しくなっており,いたるところにひし形ができあがっています.

よくみるのは,次の2種類の接線だよね..
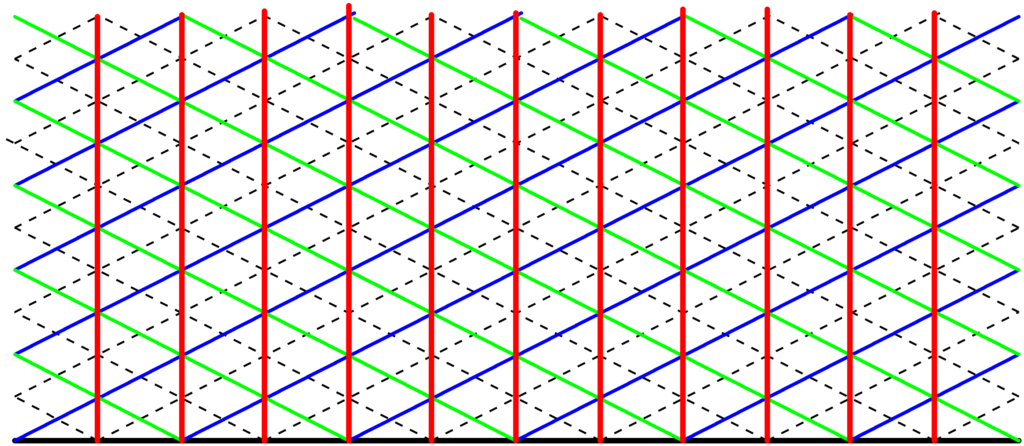
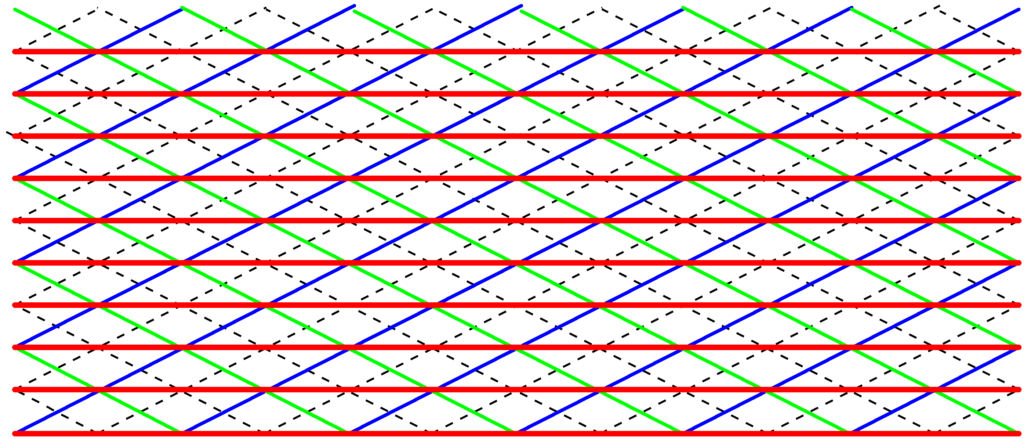

今回はどっちなの?

これだけではわかりません.
さきほどの青線,緑線はあくまでも写真なので,それぞれの波面がどのような方向に進むのかがわからないといけません.
でも,写真の山と谷,媒質の変位0の場所はわかります.
実線と実線が交わるところは山と山が重なるので,重ね合わせの原理より,より大きな山ができあがります.
破線と破線が交わるところは谷と谷が重なるので,重ね合わせの原理より,より大きな谷ができあがります.
そして,実線と破線が交わるところは山と谷が重なるので,重ね合わせの原理より,変位が0となります.

重ね合わせの原理は次のようなものだったね.
2つ以上の波がある場合,その合成波は媒質の変位の足し算となる.
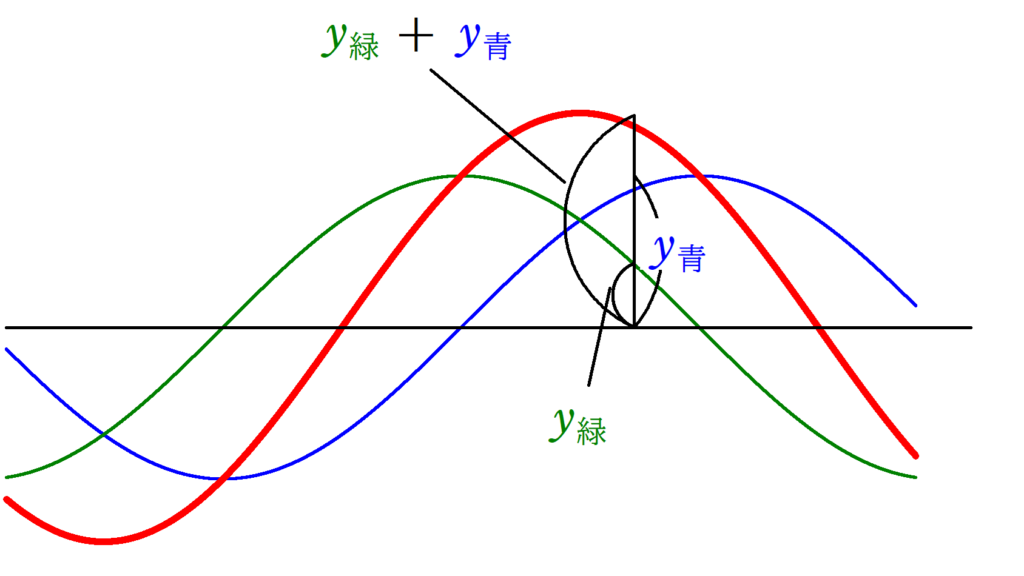
たとえば,青の波と緑の波がある場合,青の波の変位を$y_{青}$,緑の波の変位を$y_{緑}$とすれば,合成波(赤色の波)の変位は,
$y_{合成波}$$=$$y_{青}$$+$$y_{緑}$

今現在の波の様子をかくと次のようになるね.
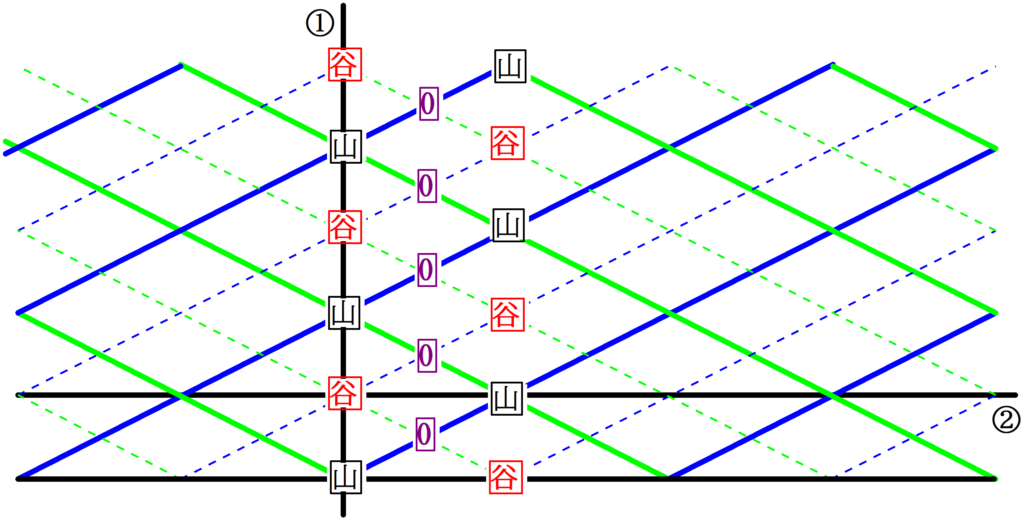

ある点を観測していると,山となったり谷となったりと,大きく振動している場所を強め合いというんだね.
そして,ある点を観測していると,その点が一切振動しない場所を弱め合いというんだね.
上図だと,①の線も②の線も山と谷が交互にあるから強め合いの点を結んだ腹線になるのかなあ??

いえ,さきほども話した通り,波の速度の向きがわからないと腹線は判明しません.
そこで,次の2つの場合について考えてみましょう.
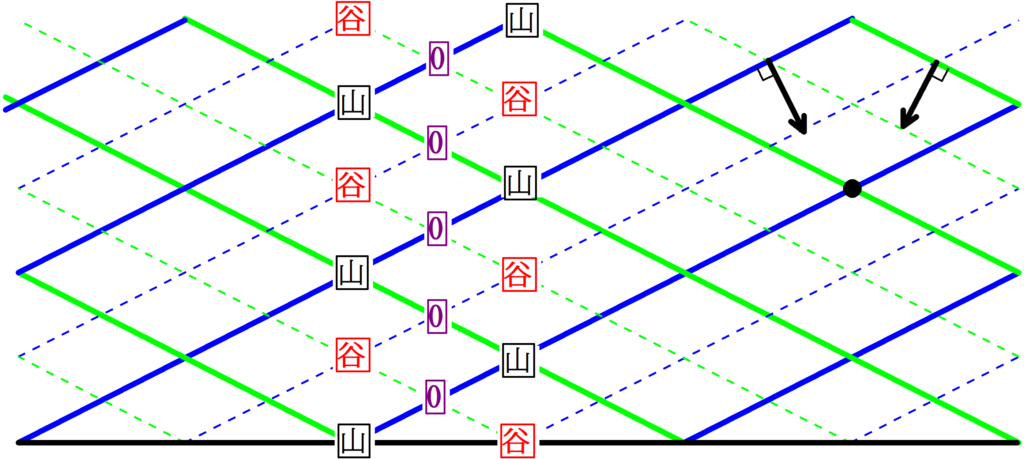
青の波と緑の波が上図の矢印の向きに動くとき,腹線をかけ.ただし,下にある黒線での反射は考えない.

速度が与えられたものの,どうやって山や谷の位置の移動の向きを調べるんだろう.

とりあえず,1つの山に着目してみましょう.
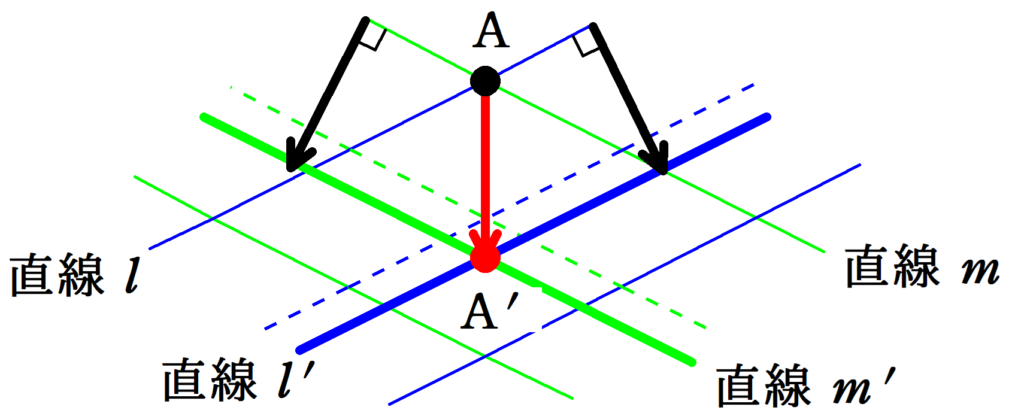

もともと,直線$l$と直線$m$の交点であった点$\rm A$の山を考えます.
それぞれの直線は,波の速度の向きを考えると,直線$l^{\prime}$,直線$m^{\prime}$に移動します.
すると,その交点である山も上図の$\rm A^{\prime}$に移動しますね.

山は図の下向きに移動しているんだね.
ということは縦のラインは山と谷が下に移動することで,ある点を観測すると,常に山と谷が交互に出てくるんだね.
だから,腹線は縦に引けるのか!

そうですね.
腹線は次のようになります.

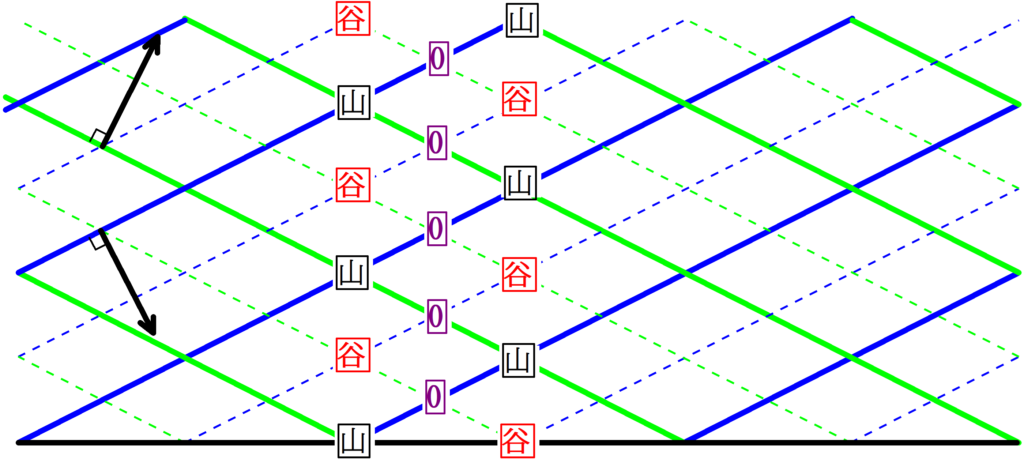
青の波と緑の波が上図の矢印の向きに動くとき,腹線をかけ.

今回も,1つの山に着目して,その山の進む方向を調べればいいんだね.
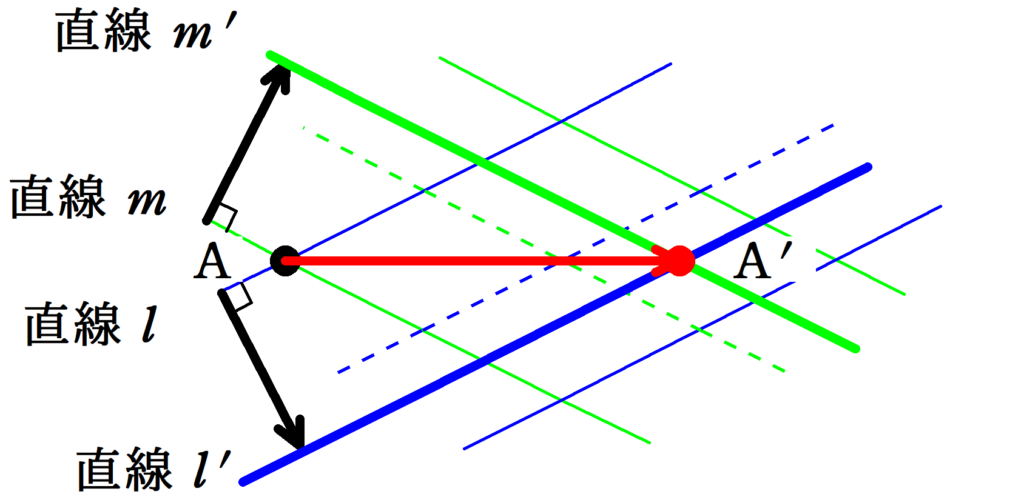

もともとは,直線$l$と直線$m$の交点だった点$\rm A$が,直線$m^{\prime}$と直線$l^{\prime}$の交点$\rm A^{\prime}$に移動するんだね.

そうですね.
すると,腹線は横に引けます.
腹線のラインはどこでも山と谷が交互に繰り返される場所となるんですね.
答えは下図のようになります.


腹線や節線を引くには,波の移動の向きが大事なんだね.
写真にある山や谷がどのような方向に移動するかを調べてみましょう!



コメント
[…] […]