[基本]単振動の演習問題⑥ 運動方程式を立てる2

NEKO

前回から単振動の運動方程式を立てる練習をはじめました．運動方程式を立てる際は，次の3つのステップを忘れずに！

運動方程式を立てる対象物体と座標を決める．
座標の+の向きに加速度$a$を設定して，位置$x$における対象物体にはたらく力を図示する．
必要であれば，力を分解し運動方程式を立てる．

また，単振動を解く流れは以下のようになります．

運動方程式を立てて，中心座標，角振動数，周期を求める．
初期条件より，座標$x$の式を求める．

それでは，問題を解きましょう．今回は2題あります．

前回の内容はこちら

問題6-1　鉛直方向の単振動の運動方程式

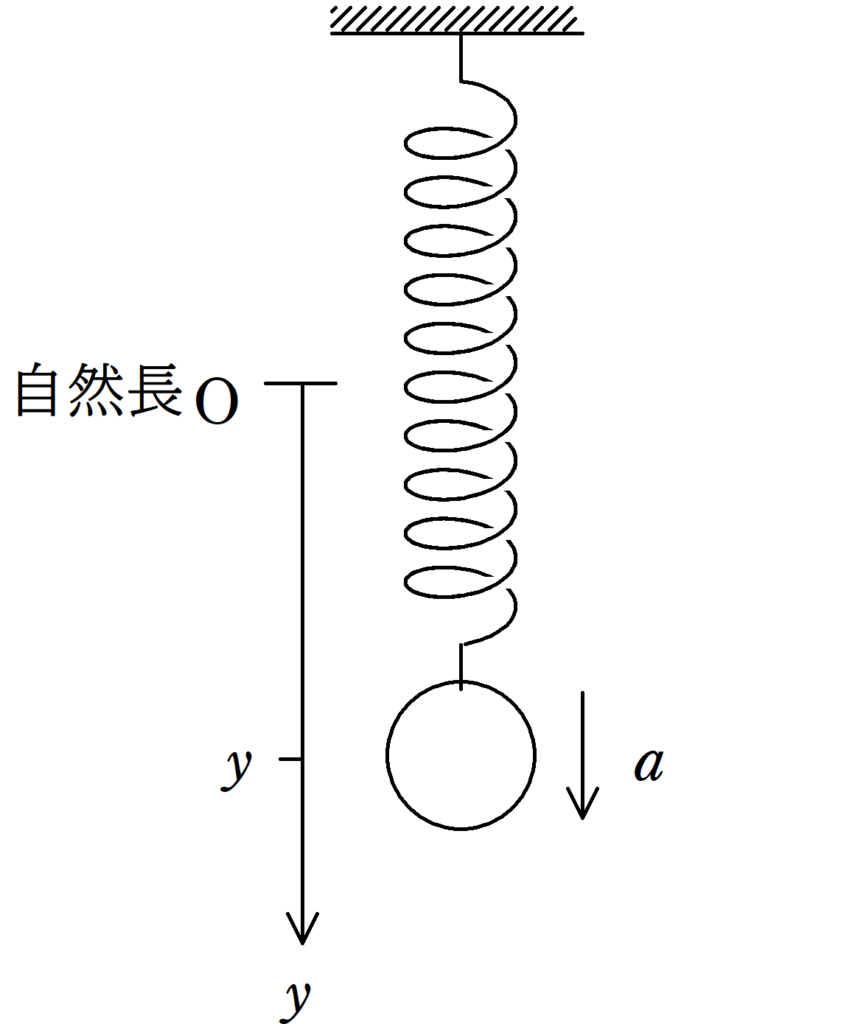
上図のように，ばね定数$k$の軽いばねの一端が天井に固定されて，他端は質量$m$の物体にとりつけられている．外力を加えて物体を自然長の位置までもっていき，静かにはなしたところ，物体は単振動を始めた．以下の問いに答えよ．ただし，自然長の位置を原点として，ばねが伸びる方向に$y$座標をとる．また，重力加速度の大きさを$g$とする．

(1)　手をはなした後の物体の運動方程式を立て，振動の中心$y_{0}$，角振動数$\omega$，振動の周期$T$をそれぞれを$m$，$k$，$g$から必要なものを用いて表せ．

(2)　手をはなした時刻を$t=0$として，時刻$t$における物体の座標$y$を$m$，$k$，$g$，$t$を用いて表せ．

<解答>

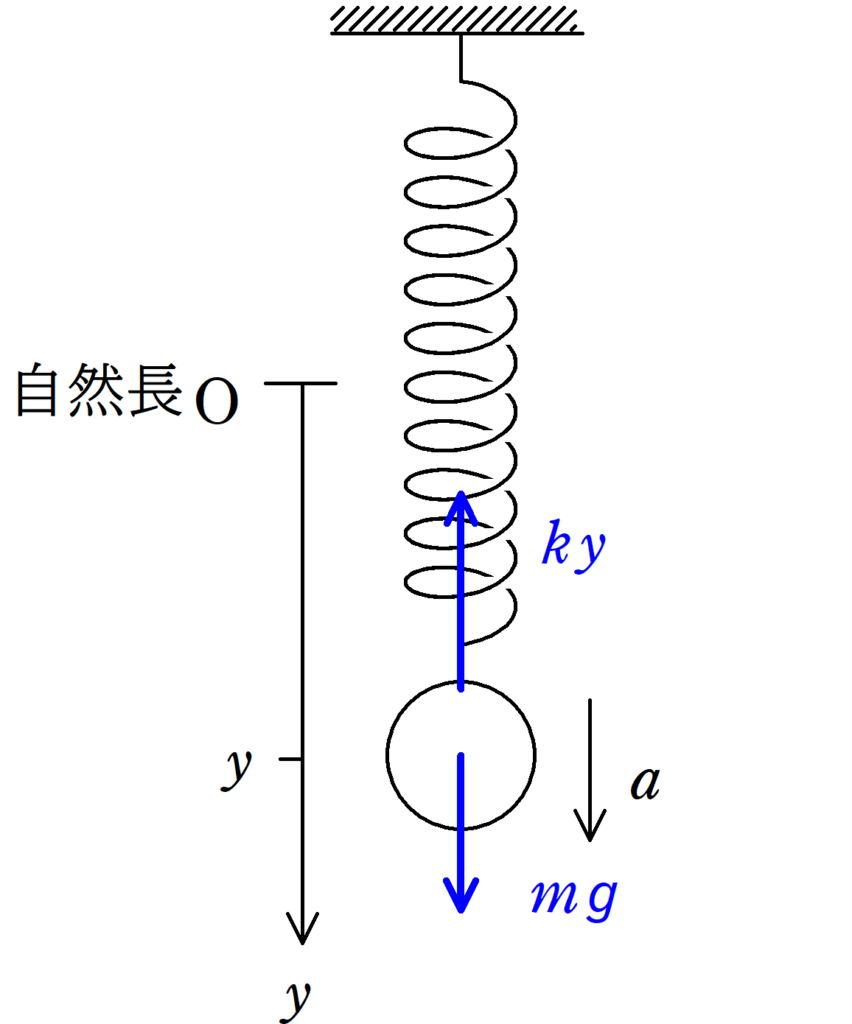
(1)　物体が$y$の位置にあるときの加速度を座標の向きに$a$と設定する．物体にはたらく力を図示すると，$+y$方向に$mg$と$y>0$のとき$ky$が$-y$方向にかかるので，運動方程式は

$ma=mg-ky=-k\left(y-\dfrac{mg}{k}\right)$

したがって，中心座標$y_{0}$，角振動数$\omega$，周期$T$はそれぞれ

$y_{0}=\dfrac{mg}{k}$，$\omega=\sqrt{\dfrac{k}{m}}$，$T=2\pi \sqrt{\dfrac{m}{k}}$

(2)　$y=0$で物体の速度が0でスタートするので，ここが振動のてっぺんになります．また，(1)より振動の中心が$y_{0}=\dfrac{mg}{k}$なので，振動の中心からてっぺんまでの距離，すなわち振幅$A$は，$A=\dfrac{mg}{k}$ということがわかります．

ここで，座標が下向きにとられていることに注意してください．今回の振動は座標としてもっとも小さいところから，上にスタートするので，$-\cos$型です．中心座標が$\dfrac{mg}{k}$なので，時刻$t$における物体の座標$y$は

$y=y_{0}-A\cos \omega t =\dfrac{mg}{k}-\dfrac{mg}{k}\cos \sqrt{\dfrac{k}{m}}t$

となります．

NEKO

続いて，斜面上の物体の単振動です．

問題6-2　斜面上の単振動の運動方程式

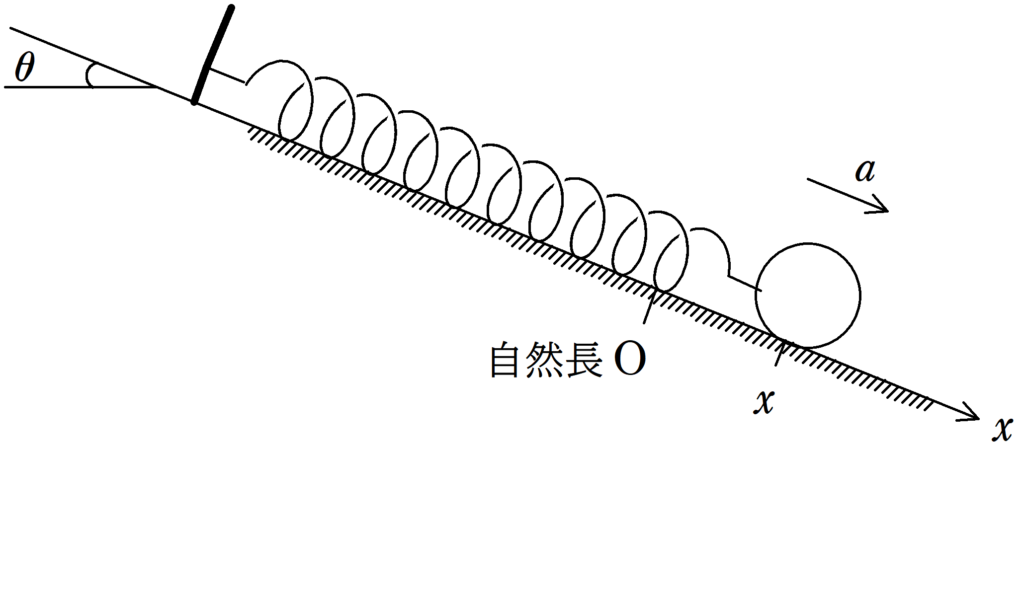
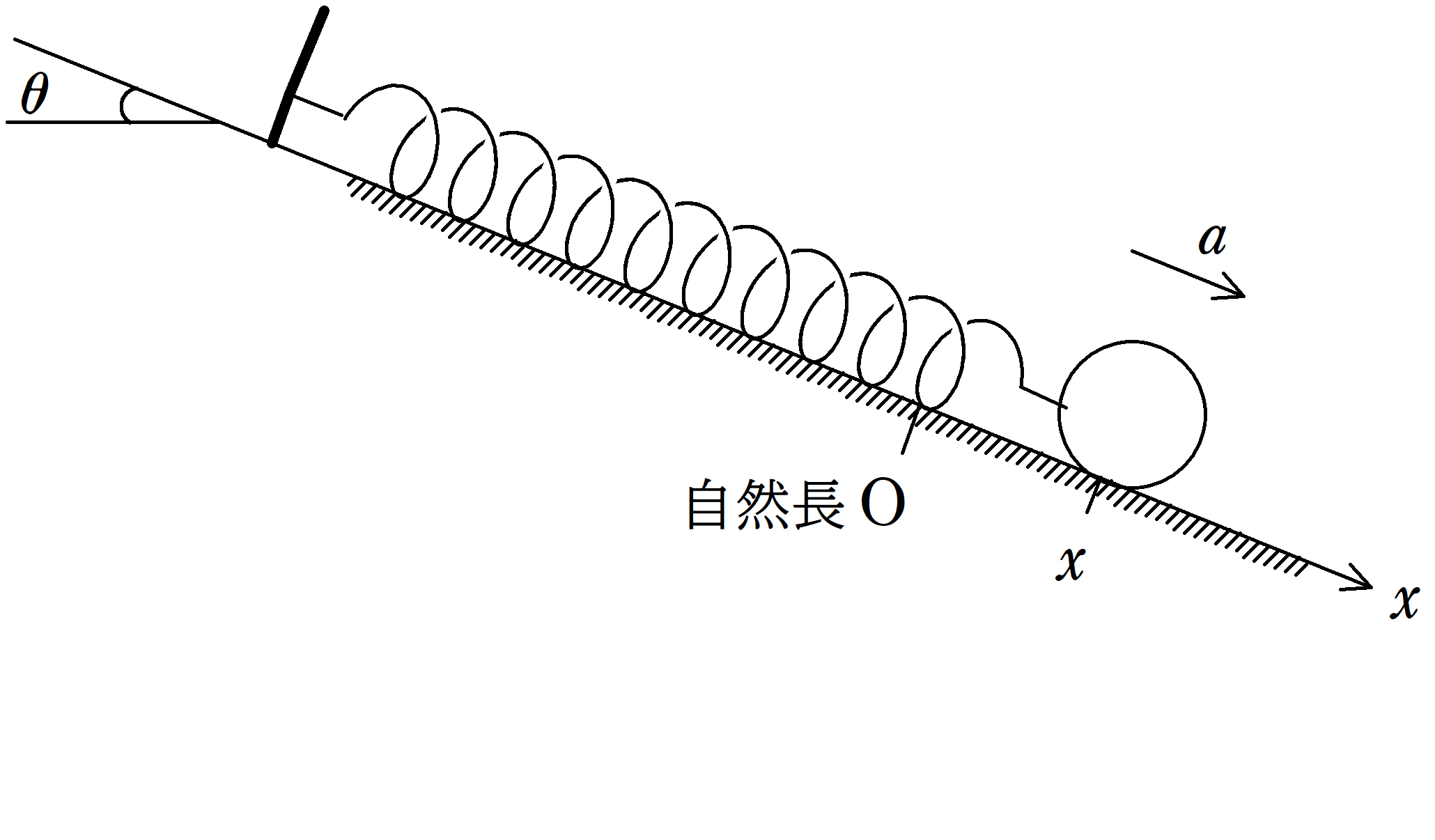
上図のように，ばね定数$k$の軽いばねの一端を傾角$\theta$の斜面上に固定されている板にとりつけ，他端を質量$m$の物体にとりつける．自然長を原点として，ばねが伸びる方向に$x$座標をとる．すると，物体は$x=x_{1}$の位置で静止した．さらに，物体を$x=2x_{1}$まで移動させ，静かに手をはなすと単振動をした．重力加速度の大きさを$g$とし，斜面はなめらかで，物体との間に摩擦力はないものとする．次の問いに答えよ．

(1)　$x_{1}$の位置を$k$，$m$，$\theta$，$g$を用いて表せ．

(2)　振動の中心$x_{0}$，角振動数$\omega$，振動の周期$T$を$k$，$m$，$\theta$，$g$から必要なものを用いて表せ．

(3)　静かに手をはなした時刻を$t=0$とする．時刻$t$における物体の座標$x$を$k$，$m$，$\theta$，$g$，$t$を用いて表せ．

<解答>

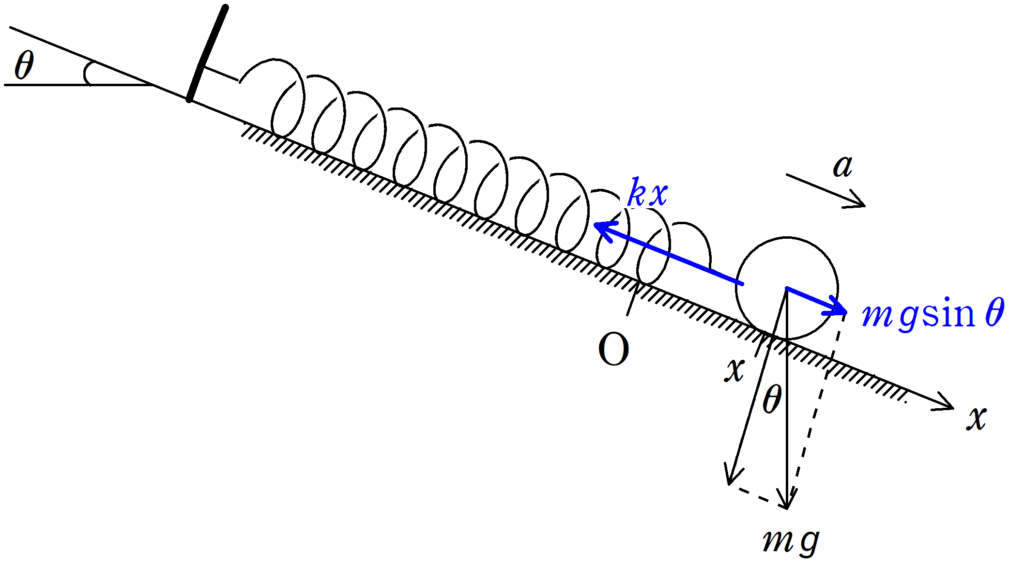
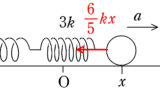
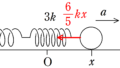
(1)　$x=x_{1}$はなにも力を加えないで静止していた位置なので，斜面に平行な方向のつり合いの式を立てます．このときの重力の斜面平行成分は$+x$方向に$mg\sin \theta$，弾性力は$-x$方向に$kx_{1}$なので，斜面に平行な方向のつり合いの式より

$mg\sin \theta =kx_{1}$　$\therefore$ $x_{1}=\dfrac{mg\sin \theta}{k}$

(2)　座標$y$における$x$軸方向の加速度を$a$とします．位置$x$における重力の斜面平行成分は$+x$方向に$mg\sin \theta$，弾性力は($x>0$のとき)$-x$方向に$kx$なので，斜面に平行な方向の運動方程式は

$ma=mg\sin \theta -kx=-k\left(x-\dfrac{mg\sin \theta}{k}\right)$

この運動方程式より，中心座標$x_{0}$，角振動数$\omega$，周期$T$は

$x_{0}=\dfrac{mg\sin \theta}{k}$，$\omega=\sqrt{\dfrac{k}{m}}$，$T=2\pi \sqrt{\dfrac{m}{k}}$

(3)　中心は$\dfrac{mg\sin \theta}{k}$で，スタートが$\dfrac{2mg\sin \theta}{k}$です．スタート地点は静かにはなされたので，初速度0であり，振動における右端っこになります．右端と中心の距離が$\dfrac{mg\sin \theta}{k}$なので，振幅は$\dfrac{mg\sin \theta}{k}$です．また，最大の座標からスタートして，$x$軸の負の向きにいくので，$\cos$型です．したがって，時刻$t$における物体の座標$x$は

$x=x_{0}+A\cos \omega t=\dfrac{mg \sin \theta}{k}+\dfrac{mg\sin \theta}{k} \cos \sqrt{\dfrac{k}{m}}t$