
今回は電磁場の領域における荷電粒子の運動です.
まずは,問題を解いてみましょう.
答えは最後にあります!
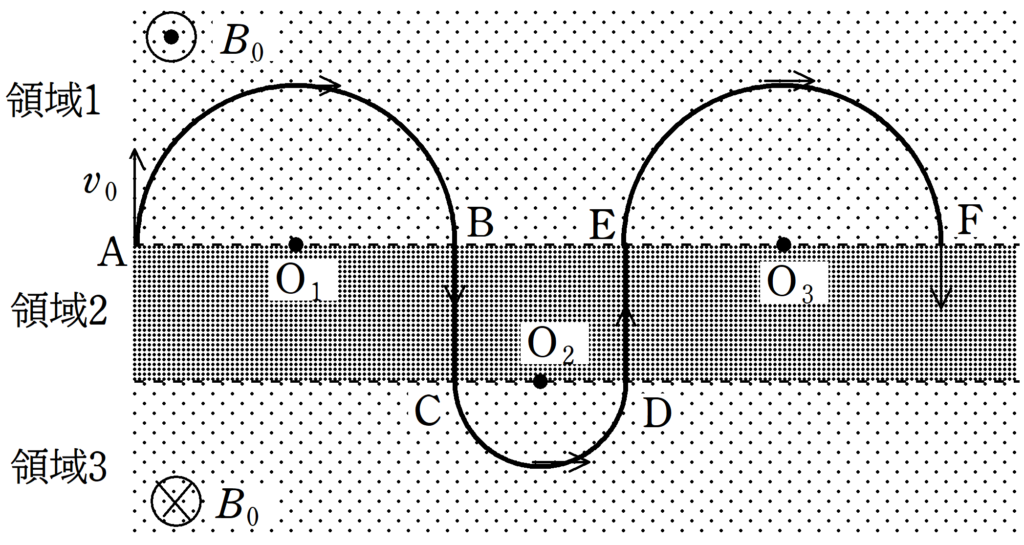
上図のように,領域1,2,3がある.領域1には画面奥から手前方向に一様な磁場がかけられており,その磁束密度の大きさは$B_{0}$である.また,領域3は画面手前から奥方向に一様な磁場がかけられており,その磁束密度の大きさは$B_{0}$である.領域2には一様な電場がかけられている.
上図のA点において,質量$m$,電荷$q$の荷電粒子に磁場と垂直な方向に初速度$v_{0}$を与えたところ,次のような運動をした.
荷電粒子はA→B→C→D→E→Fと運動し,A→BおよびC→DおよびE→Fでは等速円運動,B→CおよびD→Eは直線運動であった.
A→Bの円運動の半径とE→Fの円運動の半径がともに$2r$,C→Dの円運動の半径が$r$,BCとDEの長さがともに$d$のとき,次の問いに答えよ.
(1) 領域2の間にかけられている一様な電場の大きさと向きの組み合わせてとして適切なものを選べ.
① 向き:B→C 大きさ:$\dfrac{mv_{0}^2}{2qd}$
② 向き:B→C 大きさ:$\dfrac{3mv_{0}^2}{4qd}$
③ 向き:B→C 大きさ:$\dfrac{3mv_{0}^2}{8qd}$
④ 向き:C→B 大きさ:$\dfrac{mv_{0}^2}{2qd}$
⑤ 向き:C→B 大きさ:$\dfrac{3mv_{0}^2}{4qd}$
⑥ 向き:C→B 大きさ:$\dfrac{3mv_{0}^2}{8qd}$
(2) 荷電粒子がAからFに移動するまでにかかる時間として適切なものを次の中から選べ.ただし,(1)における電場の大きさを$E_{0}$とする.
① $\dfrac{6\pi m}{qB_{0}}+\dfrac{mv_{0}}{qE_{0}}$
② $\dfrac{6\pi m}{qB_{0}}+\dfrac{mv_{0}}{2qE_{0}}$
③ $\dfrac{6\pi m}{qB_{0}}+\dfrac{mv_{0}}{4qE_{0}}$
④ $\dfrac{3\pi m}{qB_{0}}+\dfrac{mv_{0}}{qE_{0}}$
⑤ $\dfrac{3\pi m}{qB_{0}}+\dfrac{mv_{0}}{2qE_{0}}$
⑥ $\dfrac{3\pi m}{qB_{0}}+\dfrac{mv_{0}}{4qE_{0}}$

まず,荷電粒子が磁場に対して垂直な速度をもっていたら,ローレンツ力が向心力となって等速円運動をするんだね.
ローレンツ力の復習をしよう!
磁場の大きさを$B$,磁場に垂直な速度の大きさを$v$,荷電粒子の電荷を$q$のとき,荷電粒子が受けるローレンツ力の大きさ$f$は
$f=|q|vB$
向きはフレミング左手の法則に従う.
$\clubsuit$フレミング左手の法則$\clubsuit$
親指→ローレンツ力の向き
人差し指→磁場の向き
中指→電流の向き(正電荷の動く向き,負電荷の動く向きと逆)
<解答>
(1)

(1)を解くときに,何をすればいいのかわからない人も多いかもしれません.
そういうときは,立てられる式を立てて未知な物理量を減らしましょう.
ちなみに問題文にははっきりと書いてはいないけど,Aにおいて,中心が$\rm{O_{1}}$の方向にローレンツ力が向くので,フレミング左手の法則より,中指の指(電流の向き)は,初速度の方向となります.
電荷の動く向きと電流の向きが一致しているので,$q>0$となります.
★A→Bの円運動の運動方程式について
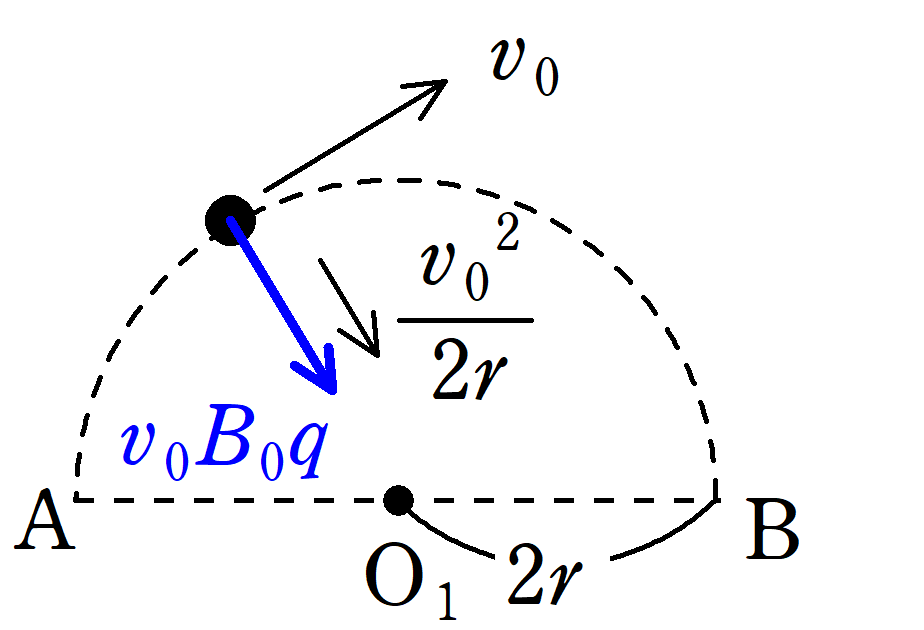
円運動の加速度は$\dfrac{(速さ)^2}{半径}$なので,円運動の運動方程式は
$m\dfrac{v_{0}^2}{2r}=v_{0}B_{0}q$
$\therefore r=\dfrac{mv_{0}}{2B_{0}q}$ $\dots (\ast)$
★C→Dの円運動の運動方程式について
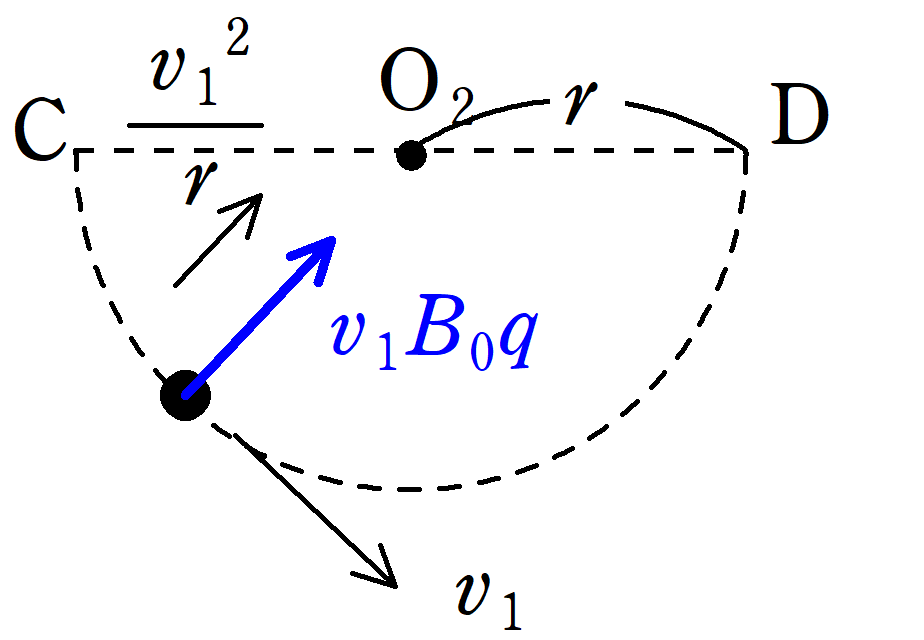
B→C間にはたらく静電気力(クーロン力)によって,速度が変化している可能性があるので,Cにおける速さを$v_{1}$としましょう.
磁場の大きさは同じく$B_{0}$であることと,円運動の半径が$r$であることから,円運動の運動方程式より
$m\dfrac{v_{1}^2}{r}=v_{1}B_{0}q$
$\therefore v_{1}=\dfrac{B_{0}qr}{m}$
$(\ast)$を上式に代入して
$v_{1}=\dfrac{B_{0}q}{m}\cdot \dfrac{mv_{0}}{2B_{0}q}=\dfrac{v_{0}}{2}$

これでCの速さがわかったね!
次に,BCの間で速度が変化した原因を考えよう!
速度の変化,つまり加速度だね.
BC間について,運動方程式を立ててみよう!
★B→Cの運動方程式
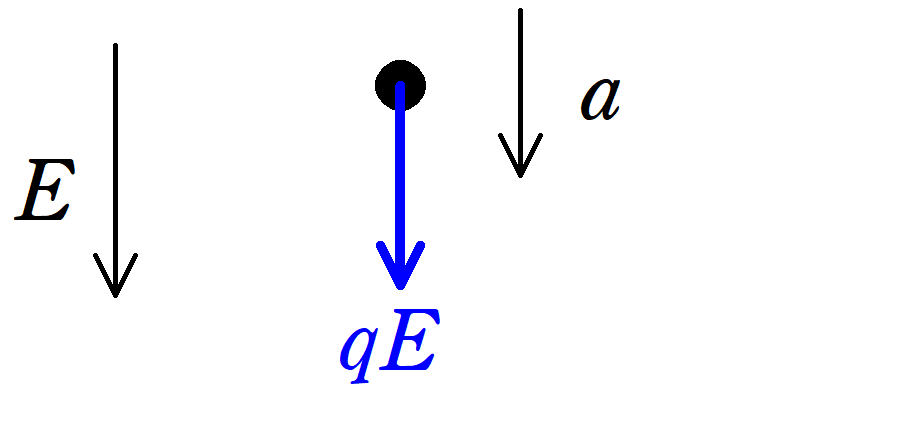
電場を$E$として,B→Cの向きにかかっていると設定しましょう.
同じく,B→Cの向きを+の向きとして,加速度を$a$とすると,運動方程式は
$ma=qE$ $\therefore a=\dfrac{qE}{m}$ $\dots (2\ast)$

$a=\dfrac{qE}{m}=$一定だから,等加速度運動の式を立てればいいね!
等加速度運動について復習しておきましょう.
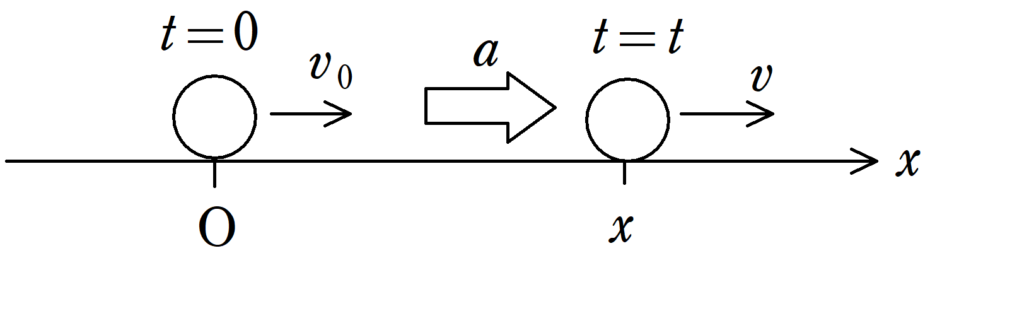
物体は加速度$a$で$x$軸上を運動している.$t=0$において,原点にある物体が,時刻$t$に座標$x$に移動した.初速度を$v_{0}$,時刻$t$における速度を$v$とするとき,次の関係式が成り立つ.
$v=v_{0}+at$
$x=v_{0}t+\dfrac{1}{2}at^2$
$v^{2}-v_{0}^{2}=2ax$

時間についての問いではないし,時間についてのヒントがあるわけではないので,3つ目の式
$v^{2}-v_{0}^{2}=2ax$
を使ってみましょう.
★BC間の等加速度運動の式
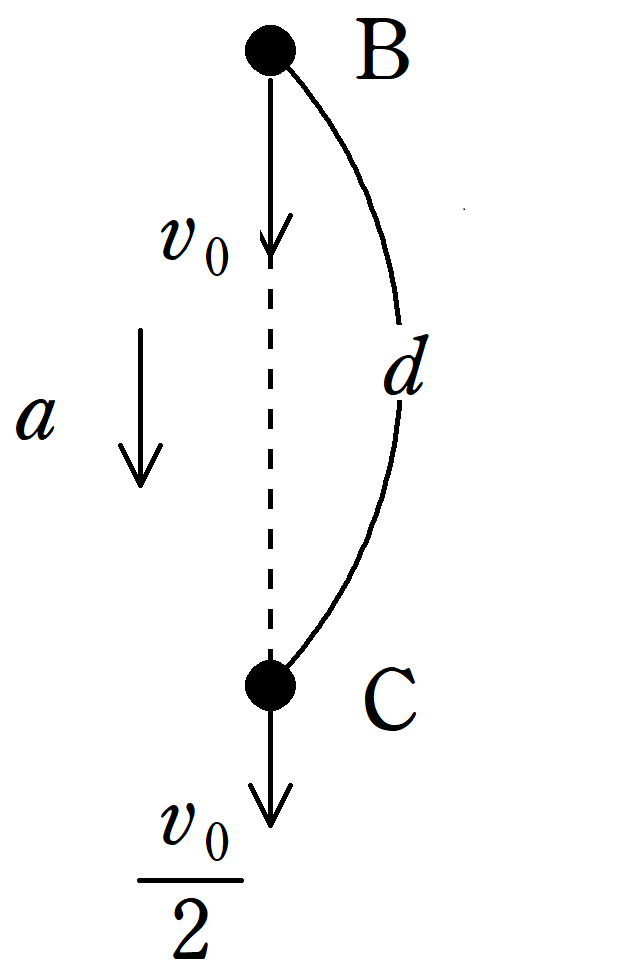
BC間に等加速度運動の式より
$(\dfrac{v_{0}}{2})^{2}-v_{0}^2=2ad$
さらに,この式に(2\ast)で得た$a=\dfrac{qE}{m}$を代入しましょう.
$(\dfrac{v_{0}}{2})^{2}-v_{0}^2=2\cdot \dfrac{qE}{m}\cdot d$
$\therefore E=-\dfrac{3mv_{0}^2}{8qd}$

$E=-\dfrac{3mv_{0}^2}{8qd}$という結果から,電場が-(マイナス)なので,設定したB→Cの方向と逆っていうことだね.
だから,(1)の答えは,⑥です.
(2)

次は時間についてです.
A→BとC→DとE→Fは円運動なので,周期の式を利用しましょう.
B→CとD→Fは等加速度運動なので,等加速度運動の式を立てます.
等速円運動のおいて,速さを$v$,半径を$r$,物体が1周するのにかかる時間を$T$(周期)とする.このとき,次の関係式が成り立つ.
$2\pi r=v\cdot T$

上の式は
円周の長さ=速さ×1周するのにかかる時間
だね.
★A→Bの間の周期の式
$T=\dfrac{2\pi \cdot 2r}{v_{0}}=\dfrac{4\pi r}{v_{0}}$
★C→Dの周期の式
$T=\dfrac{2\pi r}{\dfrac{v_{0}}{2}}=\dfrac{4\pi r}{v_{0}}$

A→B,C→Dはどちらも周期が同じだね.
E→Fに関しても半径が$2r$,速さが$v_{0}$だからやっぱり同じ周期になるよ.
A→B,C→D,E→Fを動く合計の時間$t_{1}$は
$\eqalign{t_{1}&=\dfrac{T}{2}+\dfrac{T}{2}+\dfrac{T}{2}\\&=\dfrac{3T}{2}\\&=\dfrac{6\pi r}{v_{0}}}$

しかし,このままでは×!
選択肢から選ぶ問題は選択肢をみて,使う文字を選ばなければいけないんだ.
選択肢の第1項($B_{0}$を含む方)では$v_{0}$や$r$がないね.
だから,$t_{1}$の式は,$(\ast)$の式$r=\dfrac{mv_{0}}{2B_{0}q}$を使って式を変形しましょう.
$\eqalign{t_{1}&=\dfrac{6\pi r}{v_{0}}\\&=\dfrac{6\pi \cdot \dfrac{mv_{0}}{2B_{0}q}}{v_{0}}\\&=\dfrac{3\pi m}{B_{0}q}}$ $\dots \heartsuit$

次にB→CとD→E部分の動く時間です.
こちらは等加速度運動の式を立てましょう.
★B→Cの等加速度運動の式

Bにおける速度が下向きに$v_{0}$,Cにおける速度が下向きに$\dfrac{v_{0}}{2}$であり,加速度$a$が$a=-\dfrac{qE_{0}}{m}$なので,等加速度運動の式$v=v_{0}+at$の式を立てると
$\dfrac{v_{0}}{2}=v_{0}-\dfrac{qE_{0}}{m}t$
$\therefore t=\dfrac{mv_{0}}{2qE_{0}}$

これで,BC間の運動の時間が$\dfrac{mv_{0}}{2qE_{0}}$とわかったね.
DE間も同じように計算すれば,$\dfrac{mv_{0}}{2qE_{0}}$です.
だから,BCとDE合わせた時間は
$t_{2}=\dfrac{mv_{0}}{2qE_{0}}\cdot 2=\dfrac{mv_{0}}{qE_{0}}$
なるね.

したがって,求める時間は
$t_{1}+t_{2}=\dfrac{3\pi m}{B_{0}q}+\dfrac{mv_{0}}{qE_{0}}$
です.④が正解です.
答え (1) ⑥ (2) ④


コメント